
Diagrama corpului gratuită cum se face, exemple, exerciții
A Diagrama corpului liber, diagrama corpului izolată sau diagrama forței, este o diagramă în care forțele care acționează asupra unui corp sunt reprezentate de săgeți.
Asigurați-vă că includeți în diagramă toate forțele care acționează asupra obiectului și, deoarece este o mărime vectorială, săgeata este însărcinată cu indicarea direcției și a sensului său, în timp ce lungimea sa oferă o idee despre modul sau intensitate.
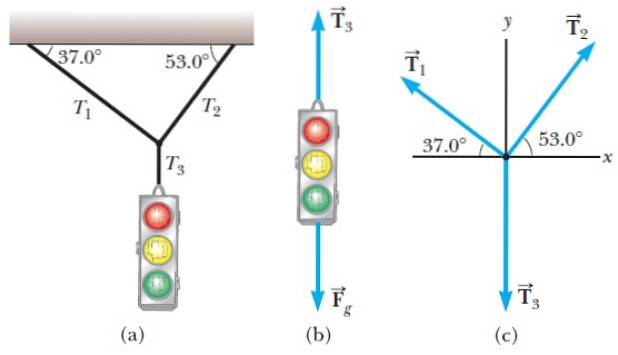
În figura 1 avem un exemplu de diagramă a corpului liber pe care urmează să îl analizăm.
Situația este următoarea: un semafor atârnat în repaus de niște cabluri (figura 1a). Două forțe acționează asupra ei, una este cea exercitată de Pământ, care este greutatea. În diagramă se notează ca Fg și acționează vertical în jos.
Cealaltă forță este tensiunea din șirul vertical, numită T3 și care merge în direcție verticală în sus, ținând semaforul și împiedicându-l să cadă la pământ.
Atunci când o problemă are mai multe obiecte, atunci este necesar să se traseze o diagramă pentru fiecare separat..
Nodul dintre frânghiile înclinate și frânghia care ține semaforul este considerat un obiect punctat, iar diagrama sa de corp liber se află în Figura 1c. Rețineți că pentru nod, tensiunea T3 este îndreptat în jos.
Este important de reținut că forțele exercitate de obiect asupra altor corpuri nu ar trebui să apară în diagrama corpului liber, ci numai cei care acționează asupra ei.
Indice articol
- 1 Exemple de diagrame cu corp liber
- 1.1 O persoană care trage un portbagaj sau un container
- 1.2 Un bloc care alunecă pe un plan înclinat
- 1.3 Mașina lui Atwood
- 2 Exercițiul a fost rezolvat
- 2.1 Soluție
- 3 Referințe
Exemple de diagrame cu corp liber
Diagrama corpului liber permite aplicarea legilor lui Newton și, odată cu acestea, determină starea de mișcare sau de repaus a obiectului asupra căruia acționează forțele. În cazul semaforului afișat, putem determina valoarea tensiunilor din cablurile care țin semaforul, cunoscând greutatea acestuia.
Odată cunoscute aceste date, sunt selectate cabluri adecvate pentru a atârna semaforul și care își îndeplinesc funcția fără a se prăbuși.
Diagramele cu corp liber sunt folosite pentru a descrie diverse situații de zi cu zi, precum acestea:
O persoană care trage un portbagaj sau un container
Este foarte frecvent ca oamenii să fie nevoiți să transporte obiecte grele precum containerul din figură. Pentru a face acest lucru, ei trebuie să exercite o forță F despre container, care în acest exemplu este orizontală și spre dreapta, care este direcția de mișcare.
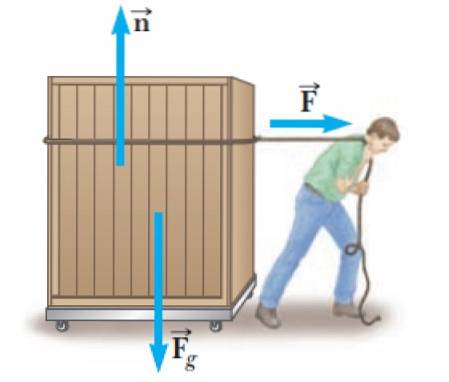
Dar aceasta nu este singura forță care acționează asupra lui, există și normalul n, exercitat de suprafața plană a platformei cu roți. Și, în cele din urmă, există greutatea acestuia: Fg, îndreptat vertical în jos.
Normalul este o forță care apare ori de câte ori două suprafețe sunt în contact și este întotdeauna perpendiculară pe suprafața care o exercită. În acest caz, platforma cu roți exercită o normală asupra containerului.
Un bloc care alunecă pe un plan înclinat
Unele birouri au masa ușor înclinată pentru a facilita luarea notelor și citirea. Are, de asemenea, un slot pentru suport pentru creion, dar cu toții am pus creionul pe masă din slot și am văzut cum alunecă pe masă.
Ce forțe acționează asupra creionului?
Aceiași acționează asupra blocului prezentat în următoarea diagramă a corpului liber:
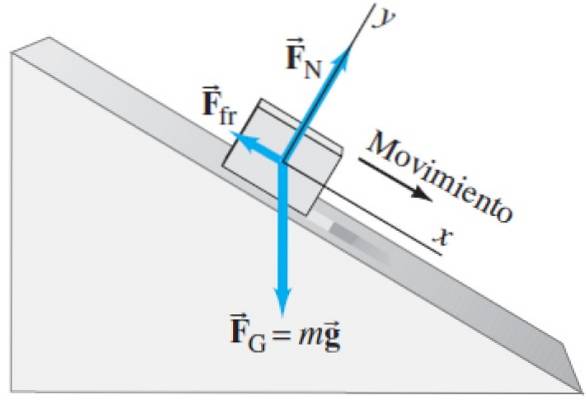
Normalul FN este forța pe care suprafața mesei o exercită asupra creionului sau blocului susținut. Spre deosebire de exemplul anterior, normalul nu este vertical, ci înclinat. Amintiți-vă că normalul este forța pe care masa o exercită asupra blocului și este perpendiculară pe acesta. Deoarece masa este înclinată, și cea normală.
Ca întotdeauna greutatea Fg este verticală, indiferent de înclinația sistemului.
Și în cele din urmă avem o nouă forță care acționează, care este fricțiunea cinetică Ffr între masă și creion sau bloc. Fricțiunea este, de asemenea, o forță de contact, dar, spre deosebire de normal, este o forță tangențială (paralelă) față de suprafață. Rețineți, de asemenea, că este întotdeauna direcționat în direcția opusă mișcării..
Mașina lui Atwood
Mașina Atwood este o mașină simplă care constă dintr-o scripete ușoară, fără frecare pe șină, prin care trece o frânghie ușoară și inextensibilă.
Două obiecte de masă m sunt atârnate de el1 si mDouă. Când unul dintre obiecte urcă, celălalt coboară, așa cum se arată în figura 4a:
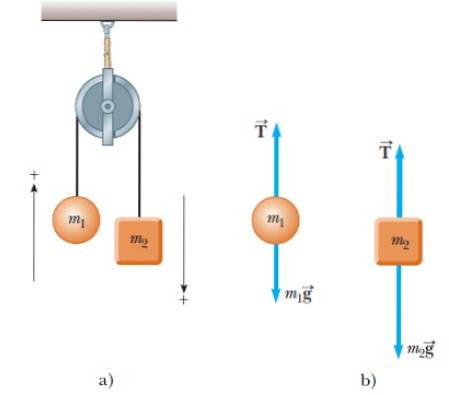
Deoarece există două obiecte, se face o diagramă cu corp liber pentru fiecare separat. Pentru ambele obiecte există doar două forțe: tensiunea în șir T și greutățile respective.
În figură, fiecare greutate este exprimată direct ca produs al masei și al accelerației. La rândul său, tensiunea este întotdeauna direcționată vertical de-a lungul frânghiei tensionate.
Exercițiul a fost rezolvat
Aplicați legile lui Newton pentru a determina accelerația cu care se deplasează masele de la mașina Atwood prezentată în secțiunea anterioară.
Soluţie
A doua lege a lui Newton afirmă că suma forțelor este egală cu produsul masei și al accelerației.
Convenția semnelor în fiecare masă poate fi diferită, așa că vom lua mișcarea ca sens pozitiv, așa cum se indică în grafic, prima masă crește și a doua cade.
În unele probleme afirmația nu oferă informații, atunci semnele trebuie atribuite în mod arbitrar și dacă rezultatul accelerației este negativ, atunci sistemul de masă se deplasează în direcția opusă celei inițial asumate.
-Pentru masa 1 (crește):
T - m1g = m1la
-Pentru masa 2 (scăzută):
-T + mDouăg = mDouăla
Ambele ecuații formează un sistem de ecuații liniare a două necunoscute, deoarece tensiunea apare cu un semn diferit în fiecare ecuație, le adăugăm pur și simplu termen cu termen, iar tensiunea anulează:
mDouăg - m1g = m1a + mDouăla
a = mDouăg - m1g / (m1 + mDouă)
Referințe
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
- Serway, R., Vulle, C. 2011. Fizica colegiului. Ediția a IX-a Cengage Learning.
- Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 1. Editorial Reverté.
- Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. Dealul Mcgraw



Nimeni nu a comentat acest articol încă.