Caracteristici de distribuție uniformă continuă, exemple, aplicații

O variabilă aleatorie are o distribuție uniformă continuă dacă probabilitatea ca aceasta să ia o valoare, într-un interval finit [a, b], este aceeași pentru orice subinterval de lungime egală.

Această distribuție este analogă distribuției uniforme discrete, care a atribuit aceeași probabilitate fiecărui rezultat al experimentului aleatoriu, dar în acest caz variabila care trebuie luată în considerare este continuă. De exemplu, experimentul care constă în selectarea unui număr real la întâmplare, între valorile a și b, urmează distribuția uniformă. Iată graficul său:

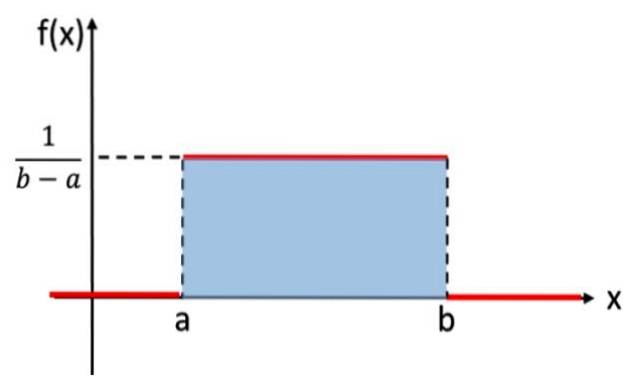
În notația matematică, distribuția uniformă continuă are o funcție de densitate definită ca o funcție bucată sau bucată, care poate fi scrisă ca:

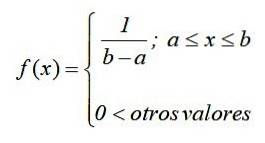
Graficul acestei funcții, cunoscut sub numele de curba sau funcția densității, este un dreptunghi, prin urmare distribuția uniformă continuă este, de asemenea, cunoscută sub numele de aspect dreptunghiular y este cea mai simplă dintre distribuțiile continue.

Aria de sub graficul unei distribuții de probabilitate este egală cu 1 și ia întotdeauna valori pozitive. Distribuția uniformă îndeplinește aceste criterii. Nu este necesar să se integreze direct pentru a verifica dacă aria este 1, deoarece aria dreptunghiului umbrit din figura 1 poate fi calculată folosind formula:

Suprafață = bază x înălțime = (b - a) x [1 / (b - a)] = 1

Cunoașterea zonei sub curba densității este foarte importantă, deoarece există o relație între zonă și probabilitatea apariției unui eveniment, care pentru această distribuție este determinată în secțiunea următoare.

Caracteristicile distribuției uniforme continue

Distribuția uniformă continuă se caracterizează prin:

Funcția de densitate

Fie X variabila aleatorie continuă, care aparține intervalului [a, b], atunci:

Funcția de distribuție

Funcția de distribuție calculează probabilitatea ca variabila aleatoare X să ia o valoare x dintre valorile posibile ale intervalului [a, b]. Pentru o distribuție continuă, se calculează în general astfel:

În cazul distribuției uniforme continue, probabilitatea F (x) este egală cu aria dreptunghiului a cărei bază este (x-a) și înălțimea acestuia este (b-a):

Matematic, dacă F (x) = Pr (X = x) următoarea funcție este stabilită în părți, conform rezultatului anterior:

În acest fel, se verifică ceea ce s-a spus anterior: probabilitatea depinde doar de valoarea lui (x-a) și nu de locația sa în intervalul [a, b]. Graficul funcției de distribuție este:

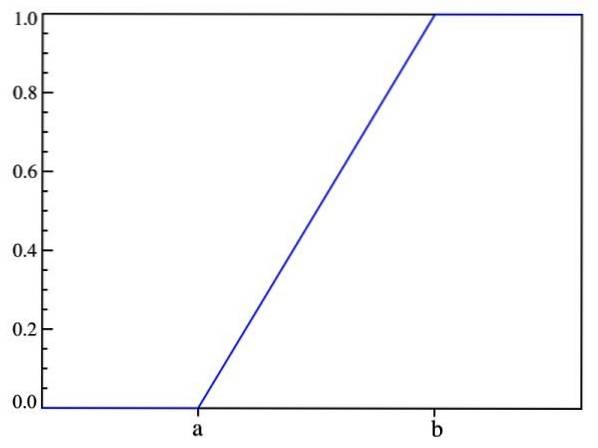
Valoarea preconizată, varianța și abaterea standard

După ce a făcut numeroase experimente cu variabila continuă aleatorie, se numește valoarea sa medie valorea estimata, este notat ca E (X) și se calculează cu următoarea integrală:

V (X) = E (X^Două) - E (X)^Două

Prin urmare:

D (X) = √ V (X)

Mediană, mod, simetrie și curtoză 

Se poate verifica cu ușurință că mediana, care este valoarea centrală a distribuției uniforme, este egală cu media și, deoarece nu există nicio valoare care să se repete mai mult decât altele, deoarece toate sunt la fel de probabile în intervalul [a, b] , moda nu există.

În ceea ce privește simetria, distribuția uniformă este simetrică și kurtosis, care este gradul în care valorile sunt concentrate în jurul centrului, este -6/5.

Exemple

Diverse situații pot fi modelate prin distribuție continuă și, astfel, comportamentul lor poate fi prezis. Aici sunt cateva exemple:

Exemplul 1

O companie care furnizează servicii electrice asigură niveluri de tensiuni distribuite uniform, între 123,0 V și 125,0 V. Acest lucru înseamnă că în priza de uz casnic este posibil să se obțină orice valoare de tensiune care aparține acelei game..

Deci, așa cum se vede mai sus, graficul funcției densității este dreptunghiul în roșu:

Calculul probabilității de a avea o tensiune în intervalul dat este foarte ușor, de exemplu, care este probabilitatea ca compania să trimită o tensiune mai mică de 123,5 V?

Această probabilitate este egală cu aria dreptunghiului umbrit în albastru:

P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25

Și care este probabilitatea ca tensiunea livrată să fie mai mare de 124,0 V?

Deoarece aria totală este egală cu 1, probabilitatea căutată este:

P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5

Are sens, deoarece 124.0 este tocmai valoarea din centrul intervalului.

Exemplul 2

O anumită variabilă aleatorie X are o distribuție uniformă în intervalul [0,100]. Decide:

a) Probabilitatea ca valoarea lui X să fie mai mică de 22.

b) Probabilitatea ca X să ia valori cuprinse între 20 și 35.

c) Valoarea preconizată, varianța și deviația standard a acestei distribuții.

Raspunde la

Este determinat în mod similar cu exemplul anterior, dar mai întâi trebuie să determinăm înălțimea dreptunghiului, amintindu-ne că aria totală trebuie să fie egală cu 1:

Suprafață = 100 × înălțime = 1

Prin urmare, dreptunghiul are o înălțime egală cu 1/100 = 0,01

P (X<22) = 22×0.01 = 0.22

Răspuns b

Probabilitatea solicitată este egală cu aria dreptunghiului a cărui lățime este (35 - 20) și a cărei înălțime este 0,01:

P (22

Dacă preferați să mergeți direct la funcția de distribuție dată mai sus, atunci trebuie doar să înlocuiți valorile din:

P (20≤X≤35) = F (35) -F (20)

Cu F (x) dat de:

F (x) = (x-a) / (b-a)

Valorile de introdus sunt:

a = 0

b = 100

F (35) = (35-0) / (100-0) = 0,35

F (20) = (20-0) / (100-0) = 0,20

P (20≤X≤35) = 0,35-0,20 = 0,15

Răspundeți c

Valoarea așteptată este:

E (X) = (a + b) / 2 = (100 + 0) / 2 = 50

Varianța este:

V (X) = (b-a)^Două/ 12 = (100-0)^Două/ 12 = 833,33

Și abaterea standard este:

D (X) = √833,33 = 28,87

Aplicații

Această distribuție este utilă atunci când se efectuează procese de simulare statistică sau când se lucrează la evenimente a căror frecvență de apariție este regulată..

Generarea de numere aleatorii

Unele limbaje de programare generează numere aleatorii între 0 și 1 și, după cum se poate vedea din exemplele anterioare, distribuția de probabilitate urmată este uniformă. În acest caz, intervalul de luat în considerare este [0,1].

Eșantionarea distribuțiilor arbitrare

Dacă aveți un experiment în care evenimentele au regularitate, așa cum s-a explicat anterior, puteți, în principiu, atribui fiecăruia aceeași probabilitate de apariție. În acest caz, modelul probabilistic al distribuției uniforme oferă informații pentru analiză..

Rotunjirea erorilor

Distribuția uniformă este, de asemenea, utilizată la rotunjirea diferențelor dintre valorile observate și valorile reale ale unei variabile, presupunând o distribuție uniformă a erorii într-un interval dat, în funcție de rotunjire, de obicei de la -0,5 la +0,5.

Referințe

1. Berenson, M. 1985. Statistici pentru management și economie. Interamericana S.A.
2. Canavos, G. 1988. Probabilitate și statistici: aplicații și metode. Dealul Mcgraw.
3. Devore, J. 2012. Probabilități și statistici pentru inginerie și știință. A 8-a. Ediție. Cengage.
4. Levin, R. 1988. Statistici pentru administratori. Al 2-lea. Ediție. Prentice hall.
5. Triola, M. 2010. Statistici elementare. 11. Ediție. Addison Wesley.
6. Walpole, R. 2007. Probabilități și statistici pentru inginerie și științe. Pearson.