
Efort normal din ce constă, cum se calculează, exemple
efort normal aplicat unui anumit material, numit și stres uniaxial, este relația care există între forța aplicată perpendicular pe o anumită suprafață și aria secțiunii transversale pe care acționează, sau sarcina pe unitate de suprafață. Matematic, dacă P este magnitudinea forței și A este aria în care se aplică, tensiunea σ este coeficientul: σ = P / A.
Unitățile de stres normal din sistemul internațional sunt newton / metruDouă, cunoscut sub numele de Pascals și abreviat Pa. Acestea sunt aceleași unități de presiune. Alte unități care apar frecvent în literatură sunt lire / inch.Două sau psi.

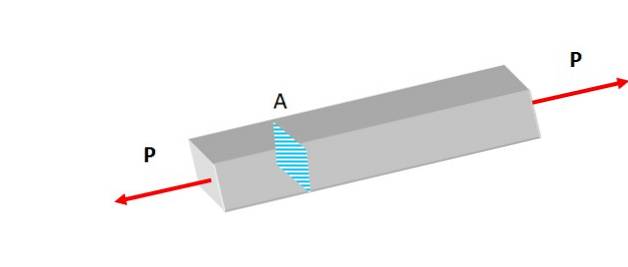
În figura 2 se aplică două forțe de aceeași mărime perpendicular pe aria secțiunii transversale, exercitând o tracțiune foarte ușoară asupra barei care tinde să o alungească..
Aceste forțe produc un stres normal care se mai numește sarcina axială centrat, deoarece linia sa de acțiune coincide cu axa axială, pe care se află centroidul.
Eforturile, indiferent dacă sunt normale sau de altă natură, apar continuu în natură. În litosferă, rocile sunt supuse gravitației și activității tectonice, suferind deformări.
În acest fel, își au originea structuri precum falduri și defecte, al căror studiu este important în exploatarea mineralelor și în ingineria civilă, pentru construcția de clădiri și drumuri, pentru a numi câteva exemple..
Indice articol
- 1 Cum se calculează?
- 2 Legea lui Hooke și stresul normal
- 3 Importanța stresului în rezistența materialelor și geologie
- 4 Exemple
- 4.1 -Exercitarea 1
- 4.2 -Exerciția 2
- 5 Referințe
Cum se calculează?
Ecuația dată la început σ = P / A permite calcularea tensiunii normale medii pe zona în cauză. Valoarea lui P este magnitudinea forței rezultate pe zona aplicată centroidului și este suficientă pentru multe situații simple.
În acest caz, distribuția forțelor este uniformă, în special în punctele îndepărtate de unde bara este supusă tensiunii sau compresiei. Dar dacă trebuie să calculați tensiunea la un anumit punct sau forțele nu sunt distribuite uniform, ar trebui să utilizați următoarea definiție:
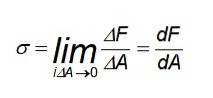
Deci, în general, valoarea stresului într-un anumit punct poate fi diferită de valoarea medie. De fapt, efortul poate varia în funcție de secțiunea care trebuie luată în considerare..
Acest lucru este ilustrat în figura următoare, în care forțele de întindere F încearcă să separe bara de echilibru în secțiuni mm Da nn.
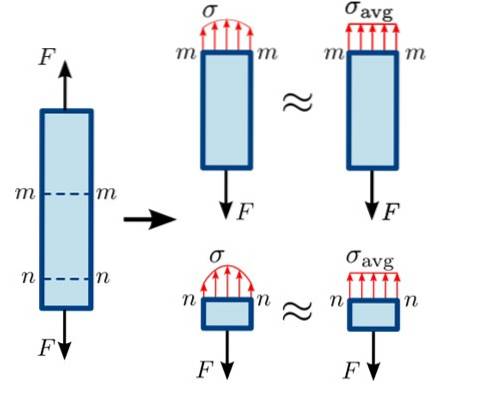
Ca secțiune nn este foarte aproape de locul în care forța F este aplicată în jos, distribuția forțelor pe suprafață nu este complet omogenă, cu cât forța este mai mică cu atât mai departe de acel punct. Distribuția este puțin mai omogenă în secțiune mm.
În orice caz, efortul normal tinde întotdeauna să se întindă sau să comprime cele două părți ale corpului care se află pe ambele părți ale planului pe care acționează. Pe de altă parte, alte eforturi diferite, cum ar fi forfecarea, tind să deplaseze și să separe aceste părți..
Legea lui Hooke și stresul normal
Legea lui Hooke afirmă că, în limitele elastice, tensiunea normală este direct proporțională cu deformarea experimentată de bară sau obiect. În acest caz:
Efort normal ∝ Deformarea unității
Fiind constanta proporționalității modulul lui Young (Y):
Stres normal (σ) = Modulul lui Young (Y) x Unitatea de deformare (ε)
σ = Y. ε
Cu ε = ΔL / L, unde ΔL este diferența dintre lungimea finală și cea inițială, care este L.
Modulul Young sau modulul de elasticitate este o caracteristică a materialului, ale cărui dimensiuni sunt aceleași cu cele ale stresului, deoarece tensiunea unitară este adimensională.
Importanța stresului în rezistența materialelor și a geologiei
Este foarte important să se determine cât de rezistente sunt materialele la stres. Pentru structurile utilizate în construcția clădirilor, precum și în proiectarea pieselor pentru diferite dispozitive, trebuie să se asigure că materialele alese își îndeplinesc în mod adecvat funcția.
Din acest motiv, materialele sunt analizate exhaustiv în laboratoare prin intermediul unor teste menite să știe câtă forță pot rezista înainte de deformare și rupere, pierzându-și astfel funcțiile. Pe baza acestui fapt, se ia decizia dacă sunt sau nu adecvate pentru a fabrica o anumită parte sau a face parte dintr-un dispozitiv..
Se crede că primul om de știință care a studiat sistematic rezistența materialelor a fost Leonardo Da Vinci. A lăsat dovezi ale testelor în care a determinat rezistența firelor prin agățarea pietrelor de diferite greutăți.
În eforturi, atât importanța forței, cât și dimensiunile structurii și modul în care este aplicată sunt importante, pentru a stabili limitele în care materialul are un comportament elastic; adică revine la forma inițială atunci când efortul încetează.
Cu rezultatele acestor teste, se fac curbe de solicitare-deformare pentru diferite tipuri de materiale, precum oțel, beton, aluminiu și multe altele..
Exemple
Următoarele exemple presupun că forțele sunt distribuite uniform și că materialul este omogen și izotrop. Aceasta înseamnă că proprietățile lor sunt aceleași în ambele direcții. Prin urmare, este valabil să se aplice ecuația σ = P / A pentru a găsi forțele.
-Exercitiul 1
În figura 3, se știe că tensiunea normală medie care acționează asupra secțiunii AB are magnitudinea 48 kPa. Găsiți: a) Magnitudinea forței F care acționează asupra CB, b) Stresul de pe secțiunea BC.
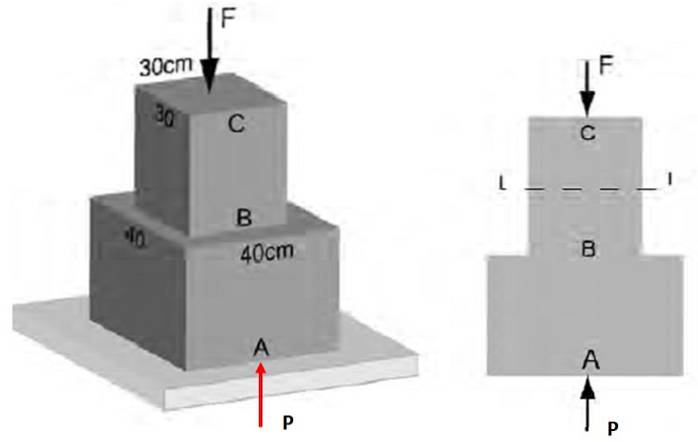
Soluţie
Deoarece structura este în echilibru static, conform celei de-a doua legi a lui Newton:
P-F = 0
Stresul normal de pe secțiunea AB are magnitudine:
σAB = P / AAB
De unde P = σAB . LAAB = 48000 Pa. (40 x 10 -Două m)Două = 7680 N
Prin urmare F = 7680 N
Stresul normal pe secțiunea BC este coeficientul dintre magnitudinea lui F și aria secțiunii transversale a acelei părți:
σÎ.Hr. = F / AÎ.Hr. = 7680 N / (30 x 10 -Două m)Două = 85,3 kPa.
-Exercițiul 2
Un fir de 150 m lungime și 2,5 mm diametru este întins cu o forță de 500 N. Găsiți:
a) Tensiunea longitudinală σ.
b) Tulpina unitară, știind că lungimea finală este de 150,125 m.
c) Modulul de elasticitate Da a acestui fir.
Soluţie
a) σ = F / A = F / π.rDouă
Raza firului este de jumătate din diametru:
r = 1,25 mm = 1,25 x 10-3 m.
Aria secțiunii transversale este π.rDouă, atunci efortul este:
σ = F / π.rDouă = 500 / (π. (1,25 x 10-3)Două Pa = 101859,2 Pa
b) ε = ΔL / L = (Lungimea finală - Lungimea inițială) / Lungimea inițială
Prin urmare:
ε = (150,125 - 150) / 150 = 0,125 / 150 = 0,000833
c) Modulul Young al firului este rezolvat cunoscând valorile lui ε și σ calculate anterior:
Y = σ / ε = 101859,2 Pa / 0,000833 = 1,22 x 108 Pa = 122 MPa.
Referințe
- Bere, F. 2010. Mecanica materialelor. Al 5-lea. Ediție. McGraw Hill. 7 - 9.
- Giancoli, D. 2006. Fizică: principii cu aplicații. 6ta Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mecanica materialelor. Al 6-lea. Ediție. Pearson Education. 22 -25
- Valera Negrete, J. 2005. Note despre fizica generală. UNAM. 87-98.
- Wikipedia. Stresul (mecanica). Recuperat de pe: wikipedia.org.


Nimeni nu a comentat acest articol încă.