
Formula de frecvență absolută, calcul, distribuție, exemplu
Frecvență absolută Este definit ca numărul de repetări ale acelorași date în cadrul setului de observații ale unei variabile numerice. Suma tuturor frecvențelor absolute este echivalentă cu totalizarea datelor.
Când aveți multe valori ale unei variabile statistice, este convenabil să le organizați în mod corespunzător pentru a extrage informații despre comportamentul acesteia. Astfel de informații sunt date de măsurile tendinței centrale și măsurile de dispersie..
În calculele acestor măsuri, datele sunt reprezentate prin frecvența cu care apar în toate observațiile..
Următorul exemplu arată cât de evidentă este frecvența absolută a fiecărei date. În prima jumătate a lunii mai, acestea au fost cele mai bine vândute mărimi de rochii de cocktail dintr-un cunoscut magazin de îmbrăcăminte pentru femei:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Câte rochii sunt vândute într-o anumită mărime, de exemplu mărimea 10? Proprietarii sunt interesați să știe să comande.
Ordonarea datelor face mai ușor de numărat, există exact 30 de observații în total, care ordonate de la cea mai mică dimensiune la cea mai mare sunt după cum urmează:
4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18
Și acum este evident că mărimea 10 se repetă de 6 ori, prin urmare, frecvența sa absolută este egală cu 6. Se efectuează aceeași procedură pentru a afla frecvența absolută a dimensiunilor rămase..
Indice articol
- 1 Formule
- 1.1 Alte frecvențe
- 2 Cum se obține frecvența absolută?
- 2.1 Intabulare
- 2.2 Tabel de frecvențe extins
- 3 Distribuția frecvenței
- 3.1 Distribuția frecvenței pentru datele grupate
- 4 Exemplu
- 5 Exercițiul a fost rezolvat
- 5.1 Soluție
- 6 Referințe
Formule
Frecvența absolută, notată ca feu, este egal cu numărul de ori pe care o anumită valoare Xeu se află în grupul de observații.
Presupunând că totalul observațiilor este de N valori, suma tuturor frecvențelor absolute trebuie să fie egală cu acest număr:
∑feu = f1 + FDouă + F3 +... fn = N
Alte frecvențe
Dacă fiecare valoare a feu împărțit la numărul total de date N, avem frecventa relativa Fr a valorii Xeu:
Fr = feu / N
Frecvențele relative sunt valori cuprinse între 0 și 1, deoarece N este întotdeauna mai mare decât orice feu, dar suma trebuie să fie egală cu 1.
Înmulțind fiecare valoare a lui f cu 100r tu ai procentul de frecvență relativă, a cărei sumă este de 100%:
Frecvența relativă procentuală = (feu / N) x 100%
De asemenea, este important frecvența cumulativă Feu până la o anumită observație, aceasta este suma tuturor frecvențelor absolute până la respectiva observație:
Feu = f1 + FDouă + F3 +... feu
Dacă frecvența acumulată este împărțită la numărul total de date N, avem frecvența relativă cumulativă, care înmulțit cu 100 dă procentul de frecvență relativă cumulată.
Cum se obține frecvența absolută?
Pentru a găsi frecvența absolută a unei anumite valori care aparține unui set de date, toate acestea sunt organizate de la cea mai mică la cea mai mare și numărul de ori când apare valoarea este numărat.
În exemplul mărimilor rochiei, frecvența absolută a mărimii 4 este de 3 rochii, adică f1 = 3. Pentru mărimea 6 s-au vândut 4 rochii: fDouă = 4. În mărimea 8 s-au vândut și 4 rochii, f3 = 4 și așa mai departe.
Intabulare
Rezultatele totale pot fi reprezentate într-un tabel care arată frecvențele absolute ale fiecăruia:
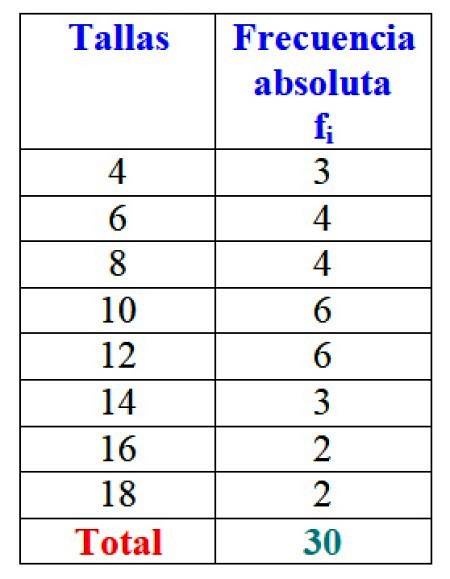
Evident, este avantajos să organizați informațiile și să le puteți accesa dintr-o privire, în loc să lucrați cu date individuale.
Important: rețineți că atunci când adăugați toate valorile coloanei feu obțineți întotdeauna numărul total de date. Dacă nu, trebuie să verificați contabilitatea, deoarece există o eroare.
Tabel de frecvențe extins
Tabelul de mai sus poate fi extins prin adăugarea celorlalte tipuri de frecvență în coloane succesive la dreapta:
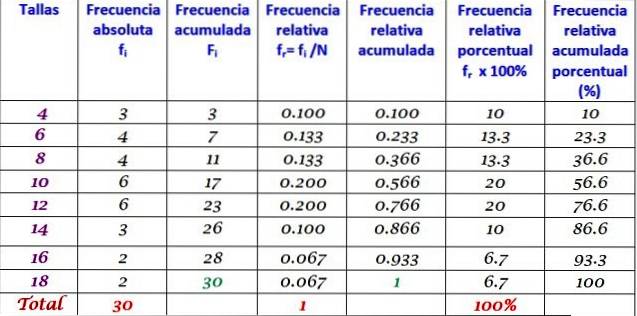
Distribuția frecvenței
Distribuția frecvenței este rezultatul organizării datelor în funcție de frecvențele lor. Când lucrați cu mai multe date, este convenabil să le grupați în categorii, intervale sau clase, fiecare cu frecvențele respective: absolute, relative, acumulate și procentuale..
Obiectivul realizării acestora este de a accesa mai ușor informațiile conținute în date, precum și de a le interpreta corect, ceea ce nu este posibil atunci când acestea sunt prezentate în nici o ordine..
În exemplul de dimensiuni, datele nu sunt grupate, deoarece nu sunt prea multe dimensiuni și pot fi ușor manipulate și contabilizate. Variabilele calitative pot fi, de asemenea, lucrate în acest fel, dar atunci când datele sunt foarte numeroase, este mai bine să lucrați grupându-le în clase.
Distribuția frecvenței pentru datele grupate
Pentru a vă grupa datele în clase de dimensiuni egale, luați în considerare următoarele:
-Dimensiunea, lățimea sau lățimea clasei: este diferența dintre cea mai mare valoare din clasă și cea mai mică.
Mărimea clasei se decide împărțind rangul R la numărul de clase care trebuie luate în considerare. Intervalul este diferența dintre valoarea maximă a datelor și cea mai mică, astfel:
Dimensiunea clasei = Rang / Numărul de clase.
-Limita clasei: interval de la limita inferioară la limita superioară a clasei.
-Marcă de clasă: este punctul de mijloc al intervalului, care este considerat reprezentativ pentru clasă. Se calculează cu semi-suma limitei superioare și limita inferioară a clasei.
-Numărul de clase: Formula Sturges poate fi utilizată:
Numărul de clase = 1 + 3.322 log N
Unde N este numărul de clase. Deoarece este de obicei un număr zecimal, este rotunjit la următorul număr întreg.
Exemplu
O mașină dintr-o fabrică mare nu funcționează din cauza unor defecțiuni recurente. Perioadele consecutive de inactivitate în minute, ale mașinii respective, sunt înregistrate mai jos, cu un total de 100 de date:
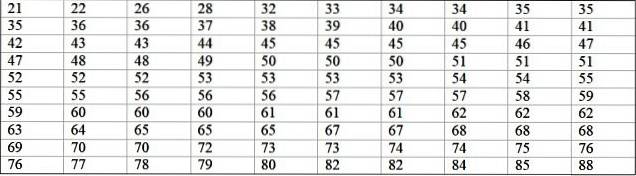
Mai întâi se determină numărul de clase:
Numărul de clase = 1 + 3.322 log N = 1 + 3.32 log 100 = 7.64 ≈ 8
Dimensiunea clasei = Gama / Numărul de clase = (88-21) / 8 = 8,375
Este, de asemenea, un număr zecimal, deci 9 este luat ca dimensiune a clasei.
Nota clasei este media dintre limitele superioare și inferioare ale clasei, de exemplu pentru clasa [20-29) există o notă de:
Nota de clasă = (29 + 20) / 2 = 24,5
Procedăm în același mod pentru a găsi notele de clasă ale intervalelor rămase.
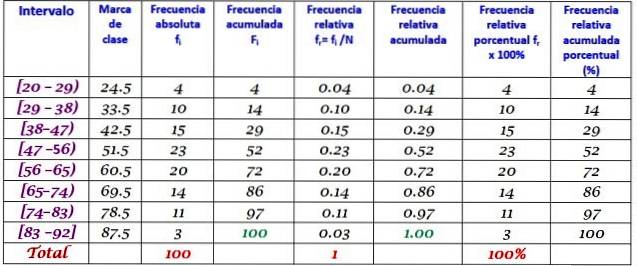
Exercițiul a fost rezolvat
40 de tineri au indicat că timpul în minute petrecut pe internet duminica trecută a fost următorul, ordonat în ordine crescătoare:
0; 12; douăzeci; 35; 35; 38; 40; Patru cinci; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Se solicită construirea distribuției de frecvență a acestor date.
Soluţie
Intervalul R al setului de date N = 40 este:
R = 220 - 0 = 220
Aplicând formula Sturges pentru a determina numărul de clase se obține următorul rezultat:
Numărul de clase = 1 + 3.322 log N = 1 + 3.32 log 40 = 6.3
Deoarece este o zecimală, întregul imediat este 7, prin urmare datele sunt grupate în 7 clase. Fiecare clasă are o lățime de:
Dimensiunea clasei = Rang / Numărul de clase = 220/7 = 31,4
O valoare apropiată și rotundă este 35, prin urmare se alege o lățime a clasei de 35.
Notele de clasă sunt calculate prin calcularea în medie a limitelor superioare și inferioare ale fiecărui interval, de exemplu, pentru intervalul [0,35):
Nota de clasă = (0 + 35) / 2 = 17,5
Procedați în același mod cu celelalte clase.
În cele din urmă, frecvențele sunt calculate conform procedurii descrise mai sus, rezultând următoarea distribuție:
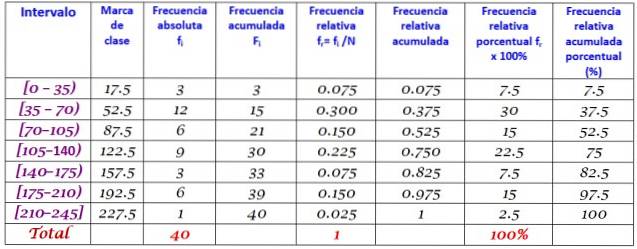
Referințe
- Berenson, M. 1985. Statistici pentru management și economie. Interamericana S.A.
- Devore, J. 2012. Probabilități și statistici pentru inginerie și știință. A 8-a. Ediție. Cengage.
- Levin, R. 1988. Statistici pentru administratori. Al 2-lea. Ediție. Prentice hall.
- Spiegel, M. 2009. Statistici. Seria Schaum. Al 4-lea Ediție. Dealul Mcgraw.
- Walpole, R. 2007. Probabilități și statistici pentru inginerie și științe. Pearson.



Nimeni nu a comentat acest articol încă.