
Formula de frecvență cumulativă, calcul, distribuție, exemple

frecvența cumulativă este suma frecvențelor absolute f, de la cea mai mică la cea care corespunde unei anumite valori a variabilei. La rândul său, frecvența absolută este de câte ori apare o observație în setul de date.
Evident, variabila de studiu trebuie să fie sortabilă. Și întrucât frecvența acumulată este obținută prin adăugarea frecvențelor absolute, se dovedește că frecvența acumulată până la ultimele date trebuie să coincidă cu totalul acestora. În caz contrar, există o eroare în calcule.

De obicei, frecvența cumulativă este notată ca Feu (sau uneori neu), pentru a-l distinge de frecvența absolută feu și este important să adăugați o coloană pentru aceasta în tabelul cu care sunt organizate datele, cunoscut sub numele de tabelul de frecvențe.
Acest lucru face mai ușor, printre altele, să urmăriți cât de multe date au fost numărate până la o anumită observație..
A Feu este, de asemenea, cunoscut sub numele de frecvența cumulativă absolută. Dacă este împărțit la datele totale, avem frecvența cumulativă relativă, a cărei sumă finală trebuie să fie egală cu 1.
Indice articol
- 1 Formule
- 1.1 Alte frecvențe acumulate
- 2 Cum se obține frecvența cumulată?
- 2.1 Cum se completează tabelul de frecvențe
- 2.2 Tabel de frecvență
- 3 Distribuția frecvenței cumulative
- 4 Exemplu
- 5 Exercițiu propus
- 5.1 Răspuns
- 6 Referințe
Formule
Frecvența cumulativă a unei valori date a variabilei Xeu este suma frecvențelor absolute f ale tuturor valorilor mai mici sau egale cu aceasta:
Feu = f1 + FDouă + F3 +... feu
Prin adăugarea tuturor frecvențelor absolute, se obține numărul total de date N, adică:
F1 + FDouă + F3 +…. + Fn = N
Operația anterioară este scrisă într-un mod rezumat prin intermediul simbolului însumării:
∑ Feu = N
Alte frecvențe cumulative
Se pot acumula și următoarele frecvențe:
-Frecventa relativa: se obține prin împărțirea frecvenței absolute feu între datele totale N:
Fr = feu / N
Dacă se adaugă frecvențele relative de la cea mai mică la cea corespunzătoare unei anumite observații, avem frecvența relativă cumulativă. Ultima valoare trebuie să fie egală cu 1.
-Procentaj frecvență relativă cumulată: frecvența relativă acumulată se înmulțește cu 100%.
F% = (feu / N) x 100%
Aceste frecvențe sunt utile pentru a descrie comportamentul datelor, de exemplu atunci când se găsesc măsurile de tendință centrală.
Cum se obține frecvența cumulată?
Pentru a obține frecvența acumulată, este necesar să ordonați datele și să le organizați într-un tabel de frecvențe. Procedura este ilustrată în următoarea situație practică:
-Într-un magazin online care vinde telefoane mobile, înregistrarea vânzărilor unei anumite mărci pentru luna martie a arătat următoarele valori pe zi:
1; Două; 1; 3; 0; 1; 0; Două; 4; Două; 1; 0; 3; 3; 0; 1; Două; 4; 1; Două; 3; Două; 3; 1; Două; 4; Două; 1; 5; 5; 3
Variabila este numărul de telefoane vândute pe zi și este cantitativ. Datele prezentate în acest mod nu sunt atât de ușor de interpretat, de exemplu, proprietarii magazinului ar putea fi interesați să știe dacă există vreo tendință, cum ar fi zilele săptămânii în care vânzările respectivei mărci sunt mai mari..
Informații de acest gen și multe altele pot fi obținute prin prezentarea datelor în mod ordonat și specificarea frecvențelor..
Cum se completează tabelul de frecvențe
Pentru a calcula frecvența cumulată, datele sunt mai întâi ordonate:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; Două; Două; Două; Două; Două; Două; Două; Două; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Apoi este construit un tabel cu următoarele informații:
-Prima coloană din stânga cu numărul de telefoane vândute, între 0 și 5 și în ordine crescătoare.
-A doua coloană: frecvența absolută, care este numărul de zile în care s-au vândut 0 telefoane, 1 telefon, 2 telefoane și așa mai departe.
-A treia coloană: frecvența acumulată, constând din suma frecvenței anterioare plus frecvența datelor care trebuie luate în considerare.
Această coloană începe cu primele date din coloana de frecvență absolută, în acest caz este 0. Pentru următoarea valoare, adăugați-o cu cea precedentă. Continuă astfel până la atingerea ultimelor date ale frecvenței acumulate, care trebuie să coincidă cu datele totale.
Tabel de frecvență
Tabelul următor prezintă variabila „numărul de telefoane vândute într-o zi”, frecvența sa absolută și calculul detaliat al frecvenței acumulate.
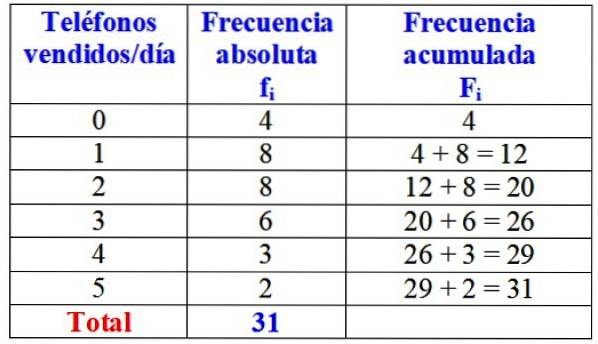
La o primă vedere, s-ar putea afirma că, pentru marca în cauză, unul sau două telefoane sunt aproape întotdeauna vândute pe zi, deoarece cea mai mare frecvență absolută este de 8 zile, ceea ce corespunde acestor valori ale variabilei. Numai în cele 4 zile ale lunii nu au vândut niciun telefon.
După cum sa menționat, tabelul este mai ușor de examinat decât datele individuale colectate inițial.
Distribuția frecvenței cumulative
O distribuție a frecvenței cumulative este un tabel care prezintă frecvențele absolute, frecvențele cumulative, frecvențele relative cumulative și frecvențele procentuale cumulative..
Deși există avantajul organizării datelor într-un tabel ca cel precedent, dacă numărul de date este foarte mare, este posibil să nu fie suficient să le organizăm așa cum se arată mai sus, deoarece dacă există multe frecvențe, devine totuși dificil să interpreta.
Problema poate fi remediată prin construirea unui distribuția frecvenței prin intervale, o procedură utilă atunci când variabila ia un număr mare de valori sau dacă este o variabilă continuă.
Aici valorile sunt grupate în intervale de amplitudine egală, numite clasă. Clasele se caracterizează prin faptul că au:
-Limita clasei: sunt valorile extreme ale fiecărui interval, există două, limita superioară și limita inferioară. În general, limita superioară nu aparține intervalului, ci următoarei, în timp ce limita inferioară aparține.
-Marcă de clasă: este punctul de mijloc al fiecărui interval și este luat ca valoare reprezentativă a acestuia.
-Lățimea clasei: Se calculează scăzând valoarea celor mai mari și mai mici date (interval) și împărțind la numărul de clase:
Lățimea clasei = Gama / Numărul de clase
Elaborarea distribuției frecvenței este detaliată mai jos..
Exemplu
Acest set de date corespunde la 40 de puncte ale unui test de matematică, pe o scară de la 0 la 10:
0; 0; 0; 1; 1; 1; 1; Două; Două; Două; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
O distribuție a frecvenței poate fi făcută cu un anumit număr de clase, de exemplu 5 clase. Trebuie avut în vedere faptul că atunci când se utilizează mai multe clase, datele nu sunt ușor de interpretat și se pierde sensul de a efectua gruparea.
Și dacă, dimpotrivă, acestea sunt grupate în foarte puține, atunci informațiile sunt diluate și o parte din acestea se pierd. Totul depinde de cantitatea de date pe care o aveți.
În acest exemplu, este o idee bună să aveți două scoruri în fiecare interval, deoarece există 10 scoruri și vor fi create 5 clase. Gama este scăderea dintre gradul cel mai înalt și cel mai mic, lățimea clasei fiind:
Lățimea clasei = (10-0) / 5 = 2
Intervalele sunt închise în stânga și deschise în dreapta (cu excepția ultimei), care este simbolizată prin paranteze și respectiv paranteze. Toate au aceeași lățime, dar nu este obligatoriu, deși este cel mai adesea.
Fiecare interval conține o anumită cantitate de elemente sau frecvență absolută, iar în coloana următoare este frecvența acumulată, în care este transportată suma. Tabelul arată, de asemenea, frecvența relativă fr (frecvența absolută între numărul total de date) și procentul de frecvență relativă fr × 100%.
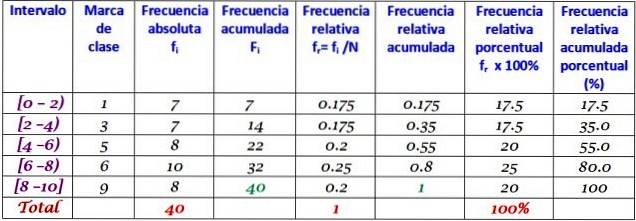
Exercițiul propus
O companie a efectuat apeluri zilnice către clienții săi în primele două luni ale anului. Datele sunt după cum urmează:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Grupați în 5 clase și construiți tabelul cu distribuția frecvenței.
Răspuns
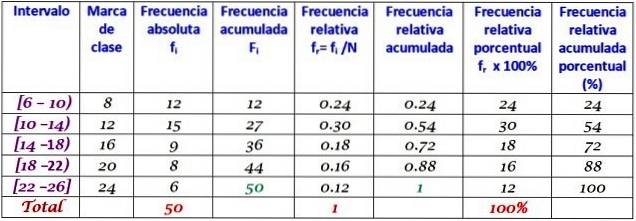
Lățimea clasei este:
(26-6) / 5 = 4
Încercați să vă dați seama înainte de a vedea răspunsul.
Referințe
- Berenson, M. 1985. Statistici pentru management și economie. Interamericana S.A.
- Devore, J. 2012. Probabilități și statistici pentru inginerie și știință. A 8-a. Ediție. Cengage.
- Levin, R. 1988. Statistici pentru administratori. Al 2-lea. Ediție. Prentice hall.
- Probabilitate și statistici. Lățimea intervalului clasei. Recuperat de pe: pedroprobabilidadyestadistica.blogspot.com.
- Spiegel, M. 2009. Statistici. Seria Schaum. Al 4-lea Ediție. Dealul Mcgraw.
- Walpole, R. 2007. Probabilități și statistici pentru inginerie și științe. Pearson.



Nimeni nu a comentat acest articol încă.