
Caracteristici funcționale constante, exemple, exerciții
funcție constantă este cel în care valoarea lui y este menținută constantă. Cu alte cuvinte: o funcție constantă are întotdeauna forma f (x) = k, Unde k este un număr real.
La graficarea funcției constante în sistemul de coordonate X y, rezultă întotdeauna o linie dreaptă paralelă cu axa orizontală sau axa X.
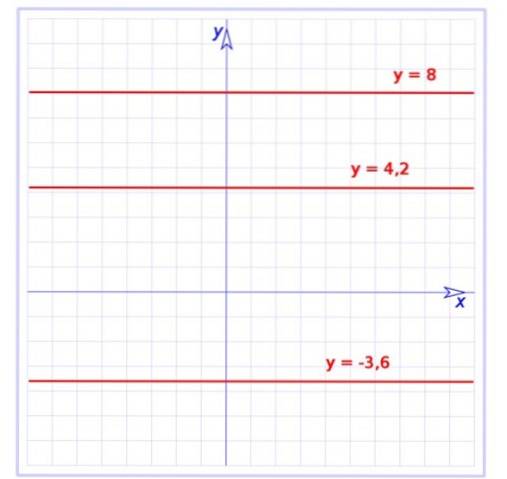
Această funcție este un caz particular al funcție afină, al cărui grafic este și o linie dreaptă, dar cu o pantă. Funcția constantă are o pantă zero, adică este o linie orizontală, așa cum se arată în figura 1.
Acolo este prezentat graficul a trei funcții constante:
f (x) = -3,6
g (x) = 4,2
h (x) = 8
Toate sunt linii paralele cu axa orizontală, prima dintre ele este sub axa menționată, în timp ce restul sunt deasupra.
Indice articol
- 1 Caracteristicile funcției constante
- 2 Exemple
- 2.1 O altă modalitate de a reprezenta o funcție constantă
- 3 exerciții rezolvate
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 3.3 - Exercițiul 3
- 3.4 - Exercițiul 4
- 3.5 - Exercițiul 6
- 4 Referințe
Caracteristicile funcției constante
Putem rezuma principalele caracteristici ale funcției constante astfel:
-Graficul său este o linie dreaptă orizontală.
-Are o singură intersecție cu axa Da, in valoare de k.
-Este continuu.
-Domeniul funcției constante (setul de valori pe care X) este mulțimea numerelor reale R.
-Calea, intervalul sau contra-domeniul (setul de valori pe care le ia variabila Da) este pur și simplu constanta k.
Exemple
Funcțiile sunt necesare pentru a stabili legături între cantități care depind într-un fel sau altul. Relația dintre ei poate fi modelată matematic, pentru a afla cum se comportă unul dintre ei când celălalt variază..
Acest lucru ajută la construirea de modele pentru multe situații și la predicții despre comportamentul și evoluția lor..
În ciuda aparentei sale simplități, funcția constantă are multe aplicații. De exemplu, atunci când vine vorba de studierea magnitudinilor care rămân constante în timp, sau cel puțin pentru un timp apreciat.
În acest fel, mărimile se comportă în situații precum următoarele:
- viteză croazieră cu o mașină care mergea pe o lungă autostradă dreaptă. Atâta timp cât nu frânați sau accelerați, mașina are o mișcare rectilinie uniformă.

-Un condensator complet încărcat deconectat de la un circuit are un sarcină constantă în timp.
-În sfârșit, o parcare forfetară menține o Preț constantă, indiferent de cât timp este parcată o mașină acolo.
Un alt mod de a reprezenta o funcție constantă
Funcția constantă poate fi alternativ reprezentată după cum urmează:
f (x) = kx0
Din moment ce orice valoare a X ridicată la 0 dă 1 ca rezultat, expresia anterioară se reduce la cea deja familiară:
f (x) = k
Desigur, acest lucru se întâmplă atâta timp cât valoarea lui k este diferit de 0.
De aceea funcția constantă este clasificată și ca a funcția polinomială de grad 0, de la exponentul variabilei X este 0.
Exerciții rezolvate
- Exercitiul 1
Răspunde la următoarele întrebări:
a) Se poate afirma că linia dată de x = 4 este o funcție constantă? Motivul răspunsului dvs..
b) Poate o funcție constantă să aibă o interceptare x?
c) Funcția f (x) = w este constantăDouă?
Raspunde la
Iată graficul liniei x = 4:
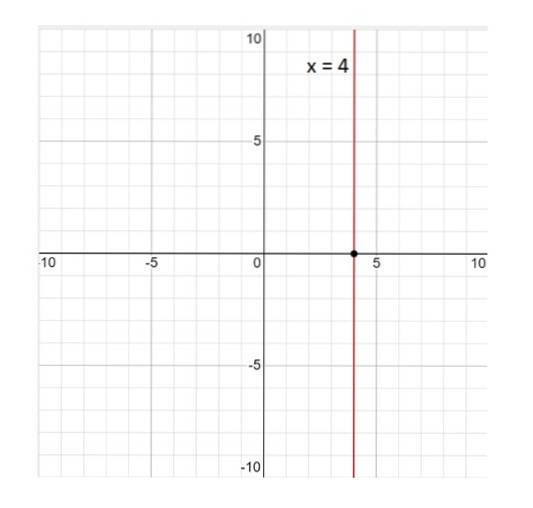
Linia x = 4 nu este o funcție; prin definiție, o funcție este o relație astfel încât la fiecare valoare a variabilei X corespunde unei singure valori de Da. Și în acest caz acest lucru nu este adevărat, deoarece valoarea x = 4 este asociat cu valori infinite ale Da. Prin urmare, răspunsul este nu.
Răspuns b
În general, o funcție constantă nu are intersecție cu axa X, decât dacă este vorba y = 0, caz în care este axa X A spus corect.
Răspundeți c
Da, de atunci w este constant, la fel și pătratul său. Ceea ce contează este că w nu depinde de variabila de intrare X.
- Exercițiul 2
Găsiți intersecția dintre funcții f (x) = 5 Da g (x) = 5x - 2
Soluţie
Pentru a găsi intersecția dintre aceste două funcții, acestea pot fi rescrise, respectiv, ca:
y = 5; y = 5x - 2
Ele sunt egalizate, obținând:
5x - 2 = 5
Ce este o ecuație liniară de gradul I, a cărei soluție este:
5x = 5 + 2 = 7
x = 7/5
Punctul de intersecție este (7 / 5,5).
- Exercițiul 3
Arătați că derivata unei funcții constante este 0.
Soluţie
Din definiția derivatului avem:

f (x + h) = k
Înlocuind în definiție:

De asemenea, dacă ne gândim la derivată ca la rata de schimbare dy / dx, funcția constantă nu suferă nicio modificare, prin urmare derivata sa este zero.
- Exercițiul 4
Găsiți integralul nedefinit al lui f (x) = k.
Soluţie

O companie de telefonie mobilă oferă servicii de internet cu tarif fix fix nelimitat pentru 15 USD pe lună. Care este funcția de preț în funcție de timp?
Soluţie
Fie P prețul de plătit în $ și în timp, care poate fi exprimat în zile. Funcția este setată astfel:
P (t) = 15
- Exercițiul 6
Următorul grafic al vitezei în raport cu timpul corespunde mișcării unei particule.

Întrebă:
a) Scrieți o expresie pentru funcția de viteză în funcție de timp v (t).
b) Găsiți distanța parcursă de mobil în intervalul de timp cuprins între 0 și 9 secunde.
Solutie la
Din graficul prezentat se poate observa că:
-v = 2 m / s în intervalul de timp cuprins între 0 și 3 secunde
-Mobilul este oprit între 3 și 5 secunde, deoarece în acest interval viteza este 0.
-v = - 3 m / s între 5 și 9 secunde.
Este un exemplu de funcție parțială sau funcție parțială, care la rândul său este compusă din funcții constante, valabile numai pentru intervalele de timp indicate. Se concluzionează că funcția căutată este:

Soluția b
Din graficul v (t), se poate calcula distanța parcursă de mobil, care este echivalentă numeric cu aria de sub / pe curbă. În acest fel:
-Distanța parcursă între 0 și 3 secunde = 2 m / s. 3 s = 6 m
-Între 3 și 5 secunde a fost oprit, prin urmare nu a parcurs nicio distanță.
-Distanța parcursă între 5 și 9 secunde = 3 m / s. 4 s = 12 m
În total, mobilul a parcurs 18 m. Rețineți că, deși viteza este negativă în intervalul cuprins între 5 și 9 secunde, distanța parcursă este pozitivă. Ce se întâmplă este că, în acel interval de timp, telefonul mobil își schimbase sensul vitezei.
Referințe
- Geogebra. Funcții constante. Recuperat de pe: geogebra.org.
- Maplesoft. Funcția constantă. Recuperat de pe: maplesoft.com.
- Wikibooks. Calcul într-o variabilă / Funcții / Funcție constantă. Recuperat de pe: es.wikibooks.org.
- Wikipedia. Funcție constantă. Recuperat de pe: en.wikipedia.org
- Wikipedia. Funcție constantă. Recuperat de pe: es.wikipedia.org.



Nimeni nu a comentat acest articol încă.