Demonstrarea identităților pitagorice, exemplu, exerciții

Sunt Identități pitagoreice toate ecuațiile trigonometrice care se mențin pentru orice valoare a unghiului și se bazează pe teorema lui Pitagora. Cea mai faimoasă dintre identitățile pitagoreice este identitatea trigonometrică fundamentală:

Sen^Două(α) + Cos^Două(α) = 1

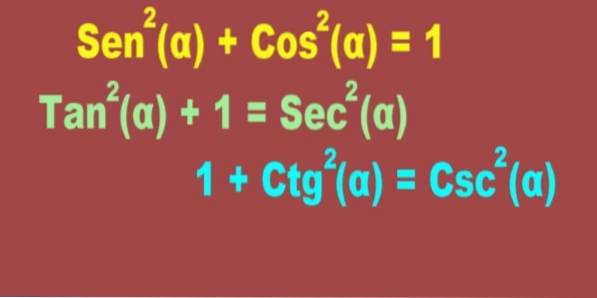
Apoi în importanță și folosesc identitatea pitagorică a tangentei și secantei:

Asa de^Două(α) + 1 = Sec^Două(α)

Și identitatea trigonometrică pitagorică care implică cotangenta și cosecanta:

1 + Ctg^Două(α) = Csc^Două(α)

Indice articol

• 1 Demo
  • 1.1 Sinusul și cosinusul
  • 1.2 Identitatea fundamentală
  • 1.3 Axa tangentă
  • 1.4 Identitatea pitagorică a tangentei
• 2 Exemplu
• 3 exerciții rezolvate
  • 3.1 Exercițiul 1
  • 3.2 Exercițiul 2
• 4 Referințe

Demonstrație

Raporturile trigonometrice sân Da cosinus sunt reprezentate într-un cerc de rază unu (1) cunoscut sub numele de cerc trigonometric. Cercul menționat are centrul la originea coordonatelor O.

Unghiurile sunt măsurate de la semi-axa pozitivă a lui X, de exemplu unghiul α din figura 2 (vezi mai jos). În sens invers acelor de ceasornic dacă unghiul este pozitiv și în sensul acelor de ceasornic dacă este un unghi negativ.

Se trasează raza cu originea O și unghiul α, care interceptează cercul unității în punctul P. Punctul P este proiectat ortogonal pe axa orizontală X dând naștere la punctul C. În mod similar, P este proiectat perpendicular pe axa verticală Y dând locul punctului S.

Avem triunghiul dreptunghiular OCP la C. 

Sinus și cosinus

Trebuie amintit că raportul trigonometric sân este definit pe un triunghi dreptunghiular după cum urmează:

Sinusul unui unghi al triunghiului este raportul sau coeficientul dintre piciorul opus unghiului și hipotenuza triunghiului.

Aplicat triunghiului OCP din figura 2 ar arăta astfel:

Sen (α) = CP / OP

dar CP = OS și OP = 1, astfel încât:

Sen (α) = OS

Aceasta înseamnă că sistemul de proiecție pe axa Y are o valoare egală cu sinusul unghiului afișat. Trebuie remarcat faptul că valoarea maximă a sinusului unui unghi (+1) apare atunci când α = 90º și minima (-1) când α = -90º sau α = 270º.

În mod similar, cosinusul unui unghi este coeficientul dintre piciorul adiacent unghiului și hipotenuza triunghiului..

Aplicat triunghiului OCP din figura 2 ar arăta astfel:

Cos (α) = OC / OP

dar OP = 1, astfel încât:

Cos (α) = OC

Aceasta înseamnă că proiecția OC pe axa X are o valoare egală cu sinusul unghiului prezentat. Trebuie remarcat faptul că valoarea maximă a cosinusului (+1) apare atunci când α = 0º sau α = 360º, în timp ce valoarea minimă a cosinusului este (-1) când α = 180º.

Identitatea fundamentală

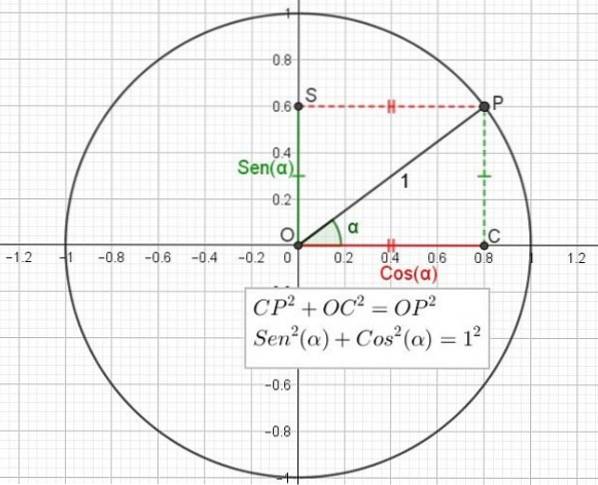
Pentru triunghiul dreptunghiular OCP în C, se aplică teorema lui Pitagora, care afirmă că suma pătratului picioarelor este egală cu pătratul hipotenuzei:

CP^Două + OC^Două = OP^Două

Dar s-a spus deja că CP = OS = Sen (α), că OC = Cos (α) și că OP = 1, astfel încât expresia anterioară poate fi rescrisă în funcție de sinus și cosinusul unghiului:

Sen^Două(α) + Cos^Două(α) = 1

Axa tangentei

Așa cum axa X din cercul trigonometric este axa cosinusului și axa Y axa sinusală, în același mod există axa tangentă (a se vedea figura 3) care este exact linia tangentă la cercul unității în punctul B coordonate (1, 0). 

Dacă doriți să cunoașteți valoarea tangentei unui unghi, trageți unghiul din semi-axa pozitivă a lui X, intersecția unghiului cu axa tangentei definește un punct Q, lungimea segmentului OQ este tangenta unghiului.

Aceasta deoarece, prin definiție, tangenta unghiului α este piciorul opus QB între piciorul adiacent OB. Adică Tan (α) = QB / OB = QB / 1 = QB.

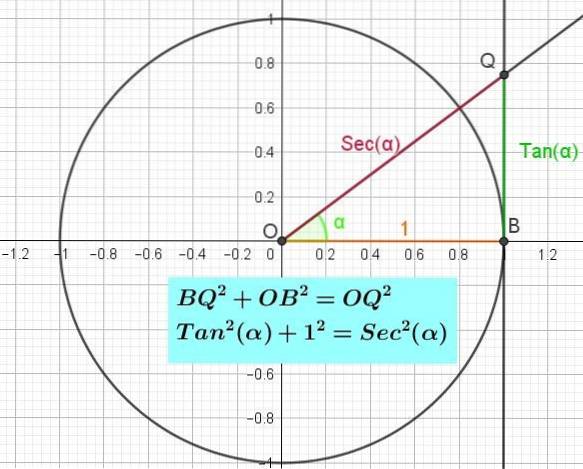
Identitatea pitagorică a tangentei

Identitatea pitagorică a tangentei poate fi dovedită luând în considerare triunghiul dreptunghi OBQ la B (Figura 3). Aplicând teorema lui Pitagora acestui triunghi avem acel BQ^Două + OB^Două = OQ^Două. Dar s-a spus deja că BQ = Tan (α), că OB = 1 și că OQ = Sec (α), astfel încât înlocuind în egalitatea pitagoreană triunghiul dreptunghi OBQ avem:

Asa de^Două(α) + 1 = Sec^Două(α).

Exemplu

Verificați dacă identitățile pitagoreice sunt sau nu îndeplinite în triunghiul dreptunghiular cu picioarele AB = 4 și BC = 3.

Soluție: picioarele sunt cunoscute, trebuie determinată hipotenuza, care este:

AC = √ (AB ^ 2 + BC ^ 2) = √ (4 ^ 2 + 3 ^ 2) = √ (16 + 9) = √ (25) = 5.

Unghiul ∡BAC se va numi α, ∡BAC = α. Acum se determină raporturile trigonometrice:

Sen α = BC / AC = 3/5 

Cos α = AB / AC = 4/5 

Deci α = BC / AB = 3/4 

Cotan α = AB / BC = 4/3 

Sec α = AC / AB = 5/4 

Csc α = AC / BC = 5/3

Începe cu identitatea trigonometrică fundamentală:

Sen^Două(α) + Cos^Două(α) = 1

(3/5) ^ 2 + (4/5) ^ 2 = 9/25 + 16/25 = (9 +16) / 25 = 25/25 = 1

Se concluzionează că este îndeplinită.

- Următoarea identitate pitagorică este cea a tangentei:

Asa de^Două(α) + 1 = Sec^Două(α)

(3/4) ^ 2 + 1 = 9/16 + 16/16 = (9 + 16) / 16 = 25/16 = (5/4) ^ 2

Și se concluzionează că identitatea tangentei este verificată.

- Într-un mod similar cu cel al cotangentei:

1 + Ctg^Două(α) = Csc^Două(α)

1+ (4/3) ^ 2 = 1 + 16/9 = 25/9 = (5/3) ^ 2

Se concluzionează că este îndeplinită și ea, cu care s-a finalizat sarcina de verificare a identităților pitagorice pentru triunghiul dat..

Exerciții rezolvate

Dovediți următoarele identități, pe baza definițiilor raporturilor trigonometrice și a identităților pitagoreice.

Exercitiul 1

Dovediți că Cos^Două x = (1 + Sen x) (1 - Sen x).

Soluţie: În partea dreaptă, se recunoaște produsul notabil al multiplicării unui binom prin conjugatul său, care, după cum se știe, este o diferență de pătrate:

Cos^Două x = 1^Două - Sen^Două X

Apoi termenul cu sinus în partea dreaptă trece în partea stângă cu semnul schimbat:

Cos^Două x + Sen^Două x = 1

Observând că identitatea trigonometrică fundamentală a fost atinsă, se concluzionează că expresia dată este o identitate, adică este adevărată pentru orice valoare a lui x.

Exercițiul 2

Pornind de la identitatea trigonometrică fundamentală și folosind definițiile raporturilor trigonometrice, demonstrați identitatea pitagorică a cosecantului.

Soluție: Identitatea fundamentală este:

Sen^Două(x) + Cos^Două(x) = 1

Ambii membri sunt împărțiți între Sen^Două(x) iar numitorul este distribuit în primul membru:

Sen^Două(x) / Sen^Două(x) + Cos^Două(x) / Sen^Două(x) = 1 / Sen^Două(X)

Este simplificat:

1 + (Cos (x) / Sen (x)) ^ 2 = (1 / Sen (x)) ^ 2

Cos (x) / Sen (x) = Cotan (x) este o identitate (non-pitagorică) care este verificată prin definiția raporturilor trigonometrice. La fel se întâmplă cu următoarea identitate: 1 / Sen (x) = Csc (x).

În cele din urmă trebuie să:

1 + Ctg^Două(x) = Csc^Două(X)

Referințe

1. Baldor J. (1973). Geometria planului și spațiului cu o introducere în trigonometrie. Cultural Central American. AC.
2. C. E. A. (2003). Elemente de geometrie: cu exerciții și geometria busolei. Universitatea din Medellin.
3. Campos, F., Cerecedo, F. J. (2014). Matematică 2. Grupo Editorial Patria.
4. IGER. (s.f.). Matematică Primul semestru Tacaná. IGER.
5. Jr. geometrie. (2014). Poligoane. Lulu Press, Inc..
6. Miller, Heeren și Hornsby. (2006). Matematică: raționament și aplicații (ediția a zecea). Pearson Education.
7. Patiño, M. (2006). Matematică 5. Editorial Progreso.
8. Wikipedia. Identități și formule de trigonometrie. Recuperat de pe: es.wikipedia.com