
Caracteristici, elemente, tipuri, aplicații ale lentilelor divergente
lentile divergente Sunt cele mai subțiri în partea centrală și mai groase la margini. În consecință, separă (diverg) razele de lumină care le lovesc paralel cu axa principală. Extensiile sale ajung să convergă în focalizarea imaginii situată în stânga obiectivului.
Lentilele divergente, sau negative așa cum sunt cunoscute, formează ceea ce se numesc imagini virtuale ale obiectelor. Au diverse aplicații. În special, în oftalmologie sunt utilizate pentru corectarea miopiei și a unor tipuri de astigmatism.

Deci, dacă sunteți miop și purtați ochelari, aveți la îndemână un exemplu perfect de lentilă divergentă..
Indice articol
- 1 Caracteristicile lentilelor divergente
- 2 Elemente de lentile divergente
- 3 Imagistica
- 4 Aplicații
- 5 tipuri
- 6 Diferențe cu lentilele convergente
- 7 Ecuația Gaussiană a lentilelor și mărirea lentilelor
- 7.1 Ecuația Gaussiană
- 8 Exercițiul a fost rezolvat
- 9 Referințe
Caracteristici divergente ale lentilelor
După cum sa explicat anterior, lentilele divergente sunt mai înguste în partea lor centrală decât la margini. În plus, în acest tip de lentile una dintre suprafețele sale este întotdeauna concavă. Acest lucru conferă acestui tip de obiectiv o serie de caracteristici.
Pentru început, prelungirea razelor care le afectează are ca rezultat imagini virtuale care nu pot fi colectate pe niciun tip de ecran. Așa este, deoarece razele care trec prin lentilă nu converg în niciun punct, deoarece diverg în toate direcțiile. În plus, în funcție de curbura lentilei, razele se vor deschide într-o măsură mai mare sau mai mică..
O altă caracteristică importantă a acestui tip de lentile este că focalizarea se află în stânga lentilei, astfel încât să fie între ea și obiect..
În plus, în obiectivele divergente imaginile sunt mai mici decât obiectul și se află între obiect și focalizare..

Elemente de lentile divergente
Atunci când le studiați, este esențial să știți ce elemente alcătuiesc lentilele în general și lentilele divergente în special..
Punctul prin care razele nu sunt deviate se numește centrul optic al unui obiectiv. Axa principală, la rândul său, este linia care unește punctul menționat și focalizarea principală, acesta din urmă fiind reprezentat de litera F.
Numele focalizării principale este punctul în care toate razele care lovesc obiectivul se găsesc paralele cu axa principală..
În acest fel, distanța dintre centrul optic și focalizare se numește distanță focală..
Centrii de curbură sunt definiți ca centrele sferelor care creează lentila; Razele de curbură fiind astfel razele sferelor care dau naștere lentilei. Și, în cele din urmă, planul central al obiectivului se numește plan optic.Imagistica
Pentru a determina grafic formarea unei imagini într-un obiectiv subțire, este necesar doar să știm direcția pe care o vor urma două din cele trei raze
a cărui traiectorie este cunoscută.
Una dintre ele este cea care lovește obiectivul paralel cu axa optică a obiectivului. Aceasta, odată refractată în obiectiv, va trece prin focalizarea imaginii. A doua dintre razele a căror cale este cunoscută este cea prin centrul optic. Aceasta nu va vedea traiectoria sa modificată.
A treia și ultima este cea care trece prin focalizarea obiectului (sau extensia acestuia traversează focalizarea obiectului) care după refracție va urma o direcție paralelă cu cea a axei optice a obiectivului..
În acest fel, în general, în lentile se va forma un tip de imagine sau altul în funcție de poziția obiectului sau corpului față de obiectiv..
Cu toate acestea, în cazul particular al lentilelor divergente, indiferent de poziția corpului în fața obiectivului, imaginea care va fi formată va avea anumite caracteristici. Și este că în lentilele divergente imaginea va fi întotdeauna virtuală, mai mică decât corpul și dreapta.
Aplicații
Faptul că pot separa lumina care trece prin ele conferă lentilelor divergente câteva calități interesante în domeniul opticii. În acest fel, pot corecta miopia și unele tipuri specifice de astigmatism.
Lentilele oftalmice divergente separă razele de lumină astfel încât, atunci când ajung la ochiul uman, să se afle mai departe. Astfel, atunci când traversează corneea și lentila, merg mai departe și pot ajunge la retină, provocând probleme de vedere la persoanele cu miopie..
Tipuri
După cum am discutat deja, lentilele convergente au cel puțin o suprafață concavă. Din această cauză, există trei tipuri de lentile divergente: biconcave, plan-concav și convex-concav..
Lentilele biconcave divergente sunt alcătuite din două suprafețe concavă, lentilele plană-concavă au o suprafață concavă și o suprafață plană, în timp ce în meniscul convex-concav sau divergent o suprafață este ușor convexă, iar cealaltă este concavă..
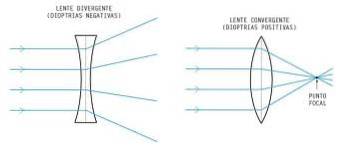
Diferențe cu lentilele convergente
La lentilele convergente, spre deosebire de ceea ce se întâmplă la lentilele divergente, grosimea scade de la centru spre margini. Astfel, în acest tip de lentile, razele de lumină care cad paralel cu axa principală sunt concentrate sau converg într-un singur punct (la focar). În acest fel, ei creează întotdeauna imagini reale ale obiectelor.
În optică, lentilele convergente sau pozitive sunt utilizate în principal pentru a corecta hipermetropia, presbiopia și unele tipuri de astigmatism.
Ecuația Gaussiană a lentilelor și mărirea lentilelor
Tipul de lentile care sunt cel mai frecvent studiate se numesc lentile subțiri. Aceasta definește toate lentilele a căror grosime este foarte mică în comparație cu razele de curbură ale suprafețelor care le limitează..
Studiul acestui tip de lentile poate fi realizat în principal prin două ecuații: ecuația Gaussiană și ecuația care permite determinarea măririi lentilei..
Ecuația Gauss
Importanța ecuației Gaussiene pentru lentilele subțiri constă în numărul mare de probleme optice de bază pe care le permite să le rezolve. Expresia sa este următoarea:
1 / f = 1 / p + 1 / q
Unde 1 / f este puterea obiectivului și f este distanța focală sau distanța de la centrul optic la focalizarea F. Unitatea de măsură a puterii unui obiectiv este dioptria (D), valoarea fiind 1 D = 1 m-1. Pe de altă parte, p și q sunt, respectiv, distanța la care este situat un obiect și distanța la care este observată imaginea sa.
Exercițiul a fost rezolvat
Un corp este plasat la 40 de centimetri de un obiectiv divergent cu distanță focală de -40 centimetri. Calculați înălțimea imaginii dacă înălțimea obiectului este de 5 cm. De asemenea, determinați dacă imaginea este dreaptă sau inversată.
Avem următoarele date: h = 5 cm; p = 40 cm; f = -40 cm.
Aceste valori sunt înlocuite în ecuația Gaussiană cu lentile subțiri:
1 / f = 1 / p + 1 / q
Și veți obține:
1 / -40 = 1/40 + 1 / q
De unde q = - 20 cm
Apoi, înlocuim rezultatul obținut anterior în ecuație cu mărirea unui obiectiv:
M = - q / p = - -20 / 40 = 0,5
Obținerea faptului că valoarea creșterii este:
M = h '/ h = 0,5
Rezolvând pentru h ', care este valoarea înălțimii imaginii, obținem:
h '= h / 2 = 2,5 cm.
Înălțimea imaginii este de 2,5 cm. De asemenea, imaginea este dreaptă de la M> 0 și diminuată, deoarece valoarea absolută a lui M este mai mică de 1.
Referințe
- Lumina (n.d.). Pe Wikipedia. Adus pe 11 aprilie 2019, de pe es.wikipedia.org.
- Lekner, John (1987). Teoria reflecției, a undelor electromagnetice și a particulelor. Springer.
- Lumina (n.d.). În Wikipedia. Adus pe 11 aprilie 2019, de pe en.wikipedia.org.
- Lentila (n.d.). Pe Wikipedia. Adus pe 11 aprilie 2019, de pe es.wikipedia.org.
- Obiectiv (optică). În Wikipedia. Adus pe 11 aprilie 2019, de pe en.wikipedia.org.
- Hecht, Eugene (2002). Optică (Ed. A 4-a). Addison Wesley.
- Tipler, Paul Allen (1994). Fizic. Ediția a 3-a. Barcelona: am inversat.



Nimeni nu a comentat acest articol încă.