
Explicația legilor lui Kepler, exerciții, experiment
Legile lui Kepler asupra mișcării planetare au fost formulate de astronomul german Johannes Kepler (1571-1630). Kepler le-a dedus pe baza profesorului său astronomul danez Tycho Brahe (1546-1601).
Brahe a compilat cu atenție date despre mișcările planetare de peste 20 de ani, cu o precizie și o precizie surprinzătoare, având în vedere că telescopul nu fusese încă inventat la acea vreme. Valabilitatea datelor dvs. este valabilă și astăzi.

Indice articol
- 1 3 legi ale lui Kepler
- 2 Legea gravitației universale și a treia lege a lui Kepler
- 3 Exerciții
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 4 experiment
- 4.1 Materiale
- 4.2 Procedură
- 5 Referințe
Cele 3 legi ale lui Kepler
Legile lui Kepler prevăd:
-Prima lege: toate planetele descriu orbite eliptice cu Soarele într-unul din focare.
-A doua lege sau lege a zonelor egale o linie direcționată de la Soare către orice planetă (rază focală), mătură zone egale în timpi egali.
-A treia lege: pătratul timpului necesar oricărei planete pentru a orbita Soarele este proporțional cu cubul distanței sale medii față de Soare.
Fi T a spus timpul, a sunat perioadă orbitală, Da r distanța medie, apoi:
TDouă este proporțional cu r3
T = k r3
Aceasta înseamnă că coeficientul TDouă/ r3 este același pentru toate planetele, ceea ce face posibilă calcularea razei orbitale, dacă se cunoaște perioada orbitală.
Cand T se exprimă în ani și r în unitățile astronomice AU *, constanta proporționalității este k = 1:
TDouă= r3
* O unitate astronomică este egală cu 150 de milioane de kilometri, care este distanța medie între Pământ și Soare. Perioada orbitală a Pământului este de 1 an.
Legea gravitației universale și a treia lege a lui Kepler
Legea universală a gravitației afirmă că magnitudinea forței gravitaționale de atracție dintre două obiecte de mase M Da m respectiv ale căror centre sunt separate de o distanță r, este dat de:
F = G mM / rDouă
G este constanta universală a gravitației și valoarea sa este G = 6,674 x 10 -unsprezece N.mDouă/ kgDouă .
Acum, orbitele planetelor sunt eliptice cu o excentricitate foarte mică.
Aceasta înseamnă că orbita nu este foarte departe de o circumferință, cu excepția în unele cazuri, cum ar fi planeta pitică Pluto. Dacă aproximăm orbitele cu forma circulară, accelerația mișcării planetei este:
lac = vDouă/ r
Având în vedere F = ma, avea:
G mM / rDouă = m.vDouă/ r
Aici v este viteza liniară a planetei din jurul Soarelui, presupusă statică și de masă M, în timp ce cel al planetei este m. Atunci:

Acest lucru explică faptul că planetele mai îndepărtate de Soare au o viteză orbitală mai mică, deoarece acest lucru depinde de 1 / √r.
Deoarece distanța pe care o parcurge planeta este aproximativ lungimea circumferinței: L = 2πr și durează un timp egal cu T, perioada orbitală, obținem:
v = 2πr / T
Echivalarea ambelor expresii pentru v oferă o expresie validă pentru TDouă, pătratul perioadei orbitale:

Și aceasta este tocmai a treia lege a lui Kepler, deoarece în această expresie parantezele 4πDouă / GM deci este constantă TDouă este proporțional cu distanța r în cuburi.
Ecuația definitivă pentru perioada orbitală se obține prin luarea rădăcinii pătrate:

Cât valorează masa Soarelui? Este posibil să aflăm prin această ecuație. Știm că perioada orbitală a Pământului este de un an și raza orbitală este de 1 UA, echivalentul a 150 de milioane de kilometri, deci avem toate datele necesare.
În ecuația noastră anterioară, rezolvăm pentru M, nu fără a converti mai întâi toate valorile în Sistemul Internațional de Unități SI:
1 an = 3,16 x 107 secunde.
1 UA = 150 milioane km = 1,5 x10unsprezece m.

Instruire
Deși Kepler a avut în vedere doar planetele atunci când a derivat faimoasele sale legi, acestea sunt valabile și pentru mișcarea sateliților și a altor corpuri din sistemul solar, așa cum vom vedea mai jos..
- Exercitiul 1
Știind că orbita lui Jupiter este de 5,19 ori cea a Pământului, găsește perioada orbitală a lui Jupiter.
Soluţie
Conform definiției Unității Astronomice, Jupiter este îndepărtat de Soare 5,19 UA, prin urmare, conform celei de a treia legi a lui Kepler:
TDouă= r3= (5,19)3 ani
Prin urmare T = (5,19)3/2 ani = 11,8 ani
- Exercițiul 2
Cometa Halley vizitează Soarele la fiecare 75,3 ani. Găsi:
a) Axa semi-majoră a orbitei sale.
b) Măsura afeliei, dacă periheliul măsoară 0,568 UA.
Soluţie
Cometa Halley vizitează Soarele la fiecare 75,3 ani. Găsi:
a) Axa semi-majoră a orbitei sale.
b) Măsura afeliei, dacă periheliul măsoară 0,568 UA.
Solutie la
Când o planetă sau orice altă stea se află în punctul cel mai apropiat de Soare, se spune că se află în periheliu, și când este mai departe, în afeliu. În cazul special al unei orbite circulare, r în a treia lege a lui Kepler este raza orbitei.
Cu toate acestea, pe orbita eliptică corpul ceresc este mai mult sau mai puțin departe de Soare, axa semi-majoră "a" fiind media dintre afeliu și periheliu:

Prin urmare, înlocuim r cu a în a treia lege a lui Kepler, care rezultă pentru Halley în:
TDouă= a3→ a = (T)2/3 → a = (75,3) 2/3 UA = 17.832 UA
Soluția b
a = ½ (Periheliu + Afelion)
17,832 = ½ (0,568+ Afelion) → Afelion = 2 x 17,832 - 0,568 UA = 35,10 AU.
Experiment
Analiza mișcării planetelor necesită săptămâni, luni și chiar ani de observare și înregistrare atentă. Dar în laborator se poate efectua un experiment la scară foarte simplu pentru a demonstra că legea lui Kepler a ariilor egale este valabilă..
Pentru aceasta, este necesar un sistem fizic în care forța care guvernează mișcarea este centrală, o condiție suficientă pentru ca legea zonelor să fie îndeplinită. Un astfel de sistem constă dintr-o masă legată de o frânghie lungă, cu celălalt capăt al firului fixat pe un suport..
Masa este mișcată un mic unghi față de poziția sa de echilibru și i se dă un ușor impuls, astfel încât să execute o mișcare ovală (aproape eliptică) în plan orizontal, ca și cum ar fi o planetă în jurul Soarelui..
Pe curba descrisă de pendul, putem demonstra că mătură zone egale în timpi egali, dacă:
-Considerăm razele vectoriale care merg de la centrul de atracție (punctul inițial de echilibru) la poziția masei.
-Și măturăm între două momente consecutive de durată egală, în două zone diferite ale mișcării.
Cu cât șirul pendulului este mai lung și cu cât unghiul este mai mic față de verticală, forța netă de refacere va fi mai orizontală și simularea seamănă cu cazul mișcării cu forță centrală într-un plan.
Apoi ovalul descris se apropie de o elipsă, cum ar fi cea pe care o parcurg planetele.
Materiale
-Fir inextensibil
-1 aluat sau bilă metalică vopsită în alb care acționează ca un bob pendul
-Rigla
-Transportor
-Aparat foto cu disc stroboscopic automat
-Suporturi
-Două surse de lumină
-O foaie de hârtie neagră sau carton
Proces
Asamblarea figurii este necesară pentru a face fotografii cu mai multe flash-uri ale pendulului pe măsură ce își urmează calea. Pentru a face acest lucru, trebuie să puneți camera chiar deasupra pendulului și a discului stroboscopic automat în fața obiectivului.
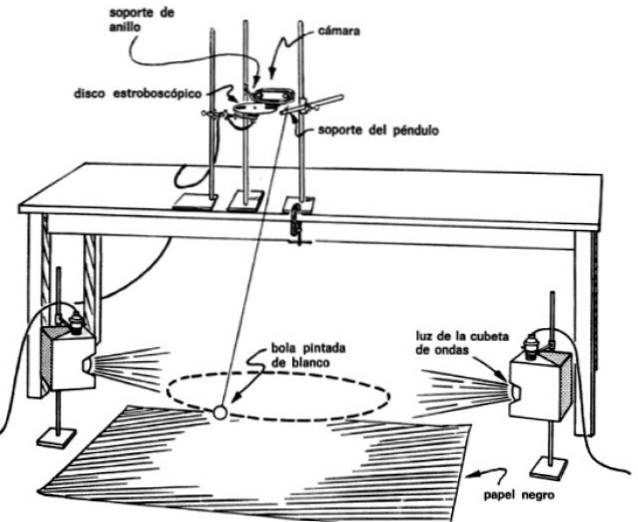
În acest fel, imaginile sunt obținute la intervale regulate de timp ale pendulului, de exemplu la fiecare 0,1 sau la fiecare 0,2 secunde, ceea ce permite să știe timpul necesar pentru a se deplasa dintr-un punct în altul..
De asemenea, trebuie să luminați în mod corespunzător masa pendulului, punând luminile pe ambele părți. Lintea trebuie vopsită în alb pentru a îmbunătăți contrastul pe fundal, care constă dintr-o hârtie neagră întinsă pe pământ.
Acum trebuie să verificați dacă pendulul mătură suprafețe egale în timpuri egale. Pentru a face acest lucru, se alege un interval de timp și punctele ocupate de pendul în intervalul menționat sunt marcate pe hârtie..
Pe imagine se trasează o linie din centrul ovalului către aceste puncte și astfel vom avea prima dintre zonele măturate de pendul, care este aproximativ un sector eliptic precum cel prezentat mai jos:
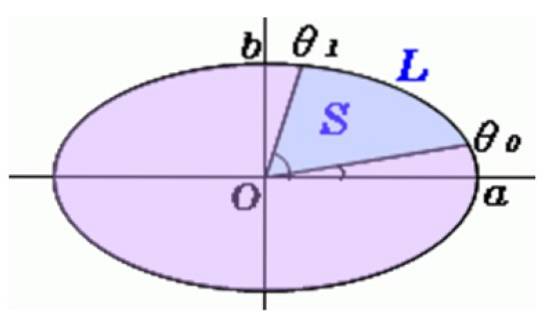
Calculul ariei secțiunii eliptice
Unghiurile sunt măsurate cu raportorul θsau Da θ1, și această formulă este utilizată pentru a găsi S, aria sectorului eliptic:
S = F (θ1) - F (θsau)
Cu F (θ) dat de:

Rețineți că la Da b sunt axele semi-majore și respectiv minore. Cititorul trebuie să se îngrijoreze doar de măsurarea atentă a semi-axelor și a unghiurilor, deoarece există calculatoare online pentru a evalua cu ușurință această expresie..
Cu toate acestea, dacă insistați să faceți calculul manual, nu uitați că unghiul θ este măsurat în grade, dar când introduceți datele în calculator, valorile trebuie exprimate în radiani.
Apoi, trebuie să marcați o altă pereche de puncte în care pendulul a inversat același interval de timp și să desenați aria corespunzătoare, calculându-i valoarea cu aceeași procedură..
Verificarea legii zonelor egale
În cele din urmă, rămâne să verificăm dacă legea zonelor este îndeplinită, adică dacă zonele egale sunt măturate în timpuri egale.
Rezultatele deviază puțin de la ceea ce era de așteptat? Trebuie întotdeauna avut în vedere faptul că toate măsurătorile sunt însoțite de eroarea lor experimentală respectivă.
Referințe
- Calculator online Keisan. Aria unui calculator de sector eliptic. Recuperat de pe: keisan.casio.com.
- Openstax. Legea lui Kepler a mișcării planetare. Recuperat de pe: openstax.org.
- PSSC. Fizica de laborator. Editorial Reverté. Recuperat de la: books.google.co.
- Palen, S. 2002. Astronomia. Seria Schaum. Dealul Mcgraw.
- Pérez R. Sistem simplu cu forță centrală. Recuperat de pe: francesphysics.blogspot.com
- Stern, cele trei legi ale mișcării planetare ale lui D. Kepler. Recuperat de pe: phy6.org.



Nimeni nu a comentat acest articol încă.