cuplu, cuplul sau momentul unei forțe este capacitatea unei forțe de a provoca o întoarcere. Etimologic primește denumirea de cuplu ca derivare a cuvântului englez cuplu, din latină torquere (răsucire).
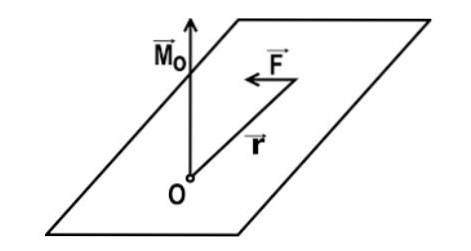
Cuplul (față de un punct dat) este magnitudinea fizică care rezultă din realizarea produsului vectorial între vectorii de poziție ai punctului în care se aplică forța și cel al forței exercitate (în ordinea indicată). Acest moment depinde de trei elemente principale.
Primul dintre aceste elemente este amploarea forței aplicate, al doilea este distanța dintre punctul în care este aplicat și punctul în raport cu care corpul se rotește (numit și brațul pârghiei), iar al treilea element este unghiul de aplicare a forței menționate.
Cu cât este mai mare forța, cu atât este mai mare rotirea. La fel se întâmplă și cu brațul pârghiei: cu cât este mai mare distanța dintre punctul în care se aplică forța și punctul în raport cu care produce virajul, cu atât acesta va fi mai mare.
Desigur, cuplul prezintă un interes special în construcții și industrie, precum și este prezent în nenumărate aplicații pentru casă, cum ar fi atunci când o piuliță este strânsă cu o cheie..
Indice articol
Expresia matematică a cuplului unei forțe față de un punct O este dată de: M = r x F
În această expresie r este vectorul care unește punctul O cu punctul P de aplicare a forței, iar F este vectorul forței aplicate.
Unitățile de măsură ale momentului sunt N ∙ m, care, deși sunt echivalente dimensional cu Joule (J), au o semnificație diferită și nu trebuie confundate.
Prin urmare, modulul cuplului ia valoarea dată de următoarea expresie:
M = r ∙ F ∙ sin α
În această expresie, α este unghiul dintre vectorul de forță și vectorul r sau brațul pârghiei. Cuplul este considerat pozitiv dacă corpul se rotește în sens invers acelor de ceasornic; dimpotrivă, este negativ atunci când se rotește în sensul acelor de ceasornic.
După cum sa menționat deja, unitatea de măsură a cuplului rezultă din produsul unei unități de forță și a unei unități de distanță. Mai exact, sistemul internațional de unități folosește metrul newton al cărui simbol este N • m.
La un nivel dimensional, newtonmetrul poate părea echivalent cu joulul; totuși, în niciun caz iulie nu trebuie folosit pentru a exprima momentele. Joule-ul este o unitate de măsurare a lucrărilor sau energiilor care, din punct de vedere conceptual, sunt foarte diferite de momentele de torsiune.
În același mod, momentul de torsiune are un caracter vector, care este atât munca scalară, cât și energia.
Din cele văzute, rezultă că cuplul unei forțe în raport cu un punct reprezintă capacitatea unei forțe sau a unui set de forțe de a modifica rotația corpului menționat în jurul unei axe care trece prin punct..
Prin urmare, momentul de torsiune generează o accelerație unghiulară pe corp și este o magnitudine a unui caracter vectorial (deci este definit dintr-un modul, o direcție și un sens) care este prezent în mecanismele care au fost supuse torsiunii sau îndoirii..
Cuplul va fi zero dacă vectorul de forță și vectorul r au aceeași direcție, deoarece în acest caz valoarea lui sin α va fi zero.
Având în vedere un anumit corp asupra căruia acționează o serie de forțe, dacă forțele aplicate acționează în același plan, cuplul rezultat din aplicarea tuturor acestor forțe; este suma momentelor de torsiune rezultate din fiecare forță. Prin urmare, este adevărat că:
MT = ∑ M = M1 + MDouă + M3 +...
Desigur, este necesar să se țină seama de criteriul semnului pentru momentele de torsiune, așa cum s-a explicat mai sus.
Cuplul este prezent în aplicații la fel de zilnic ca strângerea unei piulițe cu o cheie sau deschiderea sau închiderea unui robinet sau a unei uși.
Cu toate acestea, aplicațiile sale merg mult mai departe; cuplul se regăsește și în axele utilajului sau în rezultatul eforturilor la care sunt supuse grinzile. Prin urmare, aplicațiile sale în industrie și mecanică sunt multe și variate..
Mai jos sunt câteva exerciții pentru a facilita înțelegerea celor de mai sus.
Având în vedere următoarea figură în care distanțele dintre punctul O și punctele A și B sunt respectiv 10 cm și 20 cm:
a) Calculați valoarea modulului cuplului în raport cu punctul O dacă se aplică o forță de 20 N în punctul A.
b) Calculați care trebuie să fie valoarea forței aplicate în B pentru a obține același cuplu ca cel obținut în secțiunea anterioară.
În primul rând, este convenabil să transferați datele către unități ale sistemului internațional.
rLA = 0,1 m
rB = 0,2 m
a) Pentru a calcula modulul cuplului folosim următoarea formulă:
M = r ∙ F ∙ sin α = 0,1 ∙ 20 ∙ 1 = 2 N ∙ m
b) Pentru a determina forța solicitată, procedați în mod similar:
M = r ∙ F ∙ sin α = 0,2 ∙ F ∙ 1 = 2 N ∙ m
Rezolvând pentru F se obține că:
F = 10 N
O femeie exercită o forță de 20 N la capătul unei chei lungi de 30 cm. Dacă unghiul forței cu mânerul cheii este de 30 °, care este cuplul pe piuliță??
Se aplică următoarea formulă și se efectuează operația:
M = r ∙ F ∙ sin α = 0,3 ∙ 20 ∙ 0,5 = 3 N ∙ m
Nimeni nu a comentat acest articol încă.