Caracteristici, tipuri și exemple de mișcare rectilinie

mișcare rectilinie este cel în care telefonul mobil se mișcă de-a lungul unei linii drepte și, prin urmare, rulează într-o singură dimensiune, de aceea este numit și mișcare unidimensională. Această linie dreaptă este traiectorie sau cale urmată de obiectul în mișcare. Mașinile care se deplasează de-a lungul bulevardului din figura 1 urmează acest tip de mișcare.

Este cel mai simplu model de mișcare pe care ți-l poți imagina. Mișcările zilnice ale oamenilor, animalelor și lucrurilor combină de obicei mișcările în linie dreaptă cu mișcările de-a lungul curbelor, dar unele care sunt exclusiv rectilinii sunt frecvent observate.

Iată câteva exemple bune:

- Când alergați de-a lungul unei piste drepte de 200 de metri.

- Conducerea unei mașini pe un drum drept.

- Aruncarea liberă a unui obiect de la o anumită înălțime.

- Când o minge este aruncată vertical în sus.

Acum, obiectivul descrierii unei mișcări este atins prin specificarea caracteristicilor precum:

- Poziţie

- Deplasare

- Viteză

- Accelerare

- Vreme.

Pentru ca un observator să detecteze mișcarea unui obiect, trebuie să aibă un punct de referință (originea O) și să aibă stabilit o direcție specifică în care să se miște, care poate fi axa X, axa Da sau oricare alta.

În ceea ce privește obiectul care se mișcă, acesta poate avea un număr infinit de forme. Nu există limitări în acest sens, cu toate acestea, în tot ceea ce urmează, se va presupune că mobilul este o particulă; un obiect atât de mic încât dimensiunile sale nu sunt relevante.

Se știe că acest lucru nu este cazul obiectelor macroscopice; totuși, este un model cu rezultate bune în descrierea mișcării globale a unui obiect. În acest fel, o particulă poate fi o mașină, o planetă, o persoană sau orice alt obiect care se mișcă.

Vom începe studiul cinematicii rectilinii cu o abordare generală a mișcării și apoi vor fi studiate cazuri particulare precum cele deja numite..

Indice articol

• 1 Caracteristicile generale ale mișcării rectilinii
  • 1.1 Poziție
  • 1.2 Deplasarea
  • 1.3 Distanța parcursă
  • 1.4 Viteza medie
  • 1.5 Viteza instantanee
  • 1.6 Viteza
  • 1.7 Accelerația medie și accelerația instantanee
• 2 tipuri
  • 2.1 Mișcare cu accelerație constantă
  • 2.2 Mișcări orizontale și mișcări verticale
• 3 Exemple lucrate
  • 3.1 Exemplul 1
  • 3.2 Exemplul 2
• 4 Referințe

Caracteristicile generale ale mișcării rectilinii

Următoarea descriere este generală și se aplică oricărui tip de mișcare unidimensională. Primul lucru este să alegeți un sistem de referință. Linia de-a lungul căreia are loc mișcarea va fi axa X. Parametrii de mișcare:

Poziţie

Este vectorul care merge de la origine la punctul în care se află obiectul la un moment dat. În figura 2, vectorul X₁ indică poziția mobilului atunci când este în coordonată P₁ iar el la timp t₁. Unitățile vectorului de poziție din sistemul internațional sunt metri.

Deplasare

Deplasarea este vectorul care indică schimbarea poziției. În figura 3, mașina s-a deplasat din poziție P₁ a pozitiona P_Două, de aceea deplasarea sa este ΔX = X_Două - X₁. Deplasarea este scăderea a doi vectori, este simbolizată prin litera greacă Δ („delta”) și este la rândul său un vector. Unitățile sale din sistemul internațional sunt metri.

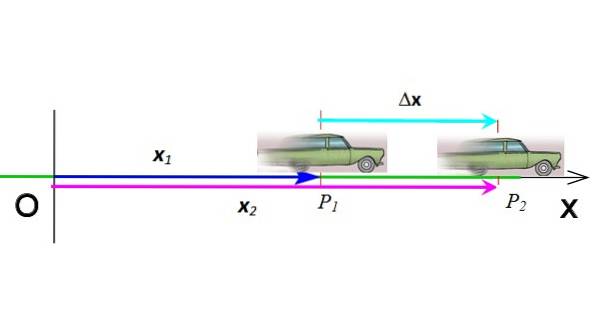
Vectorii sunt notați cu caractere aldine în textul tipărit. Dar, având aceeași dimensiune, dacă doriți, puteți face fără notația vectorială.

Distanta parcursa

Distanţă d parcurs de obiectul în mișcare este valoarea absolută a vectorului de deplasare:

d = ΙΔXΙ = ΔX

Fiind o valoare absolută, distanța parcursă este întotdeauna mai mare sau egală cu 0 și unitățile sale sunt aceleași cu cele de poziție și deplasare. Notarea valorii absolute se poate face cu bare modulo sau pur și simplu prin eliminarea tipului aldin în textul tipărit.

Viteza medie

Cât de repede se schimbă poziția? Există telefoane mobile lente și mobile rapide. Cheia a fost întotdeauna viteza. Pentru a analiza acest factor, se analizează poziția X funcția timpului t.

Viteza medie v_m (vezi figura 4) este panta liniei secante (fuchsia) către curbă X vs. t și oferă informații globale despre mișcarea mobilului în intervalul de timp luat în considerare.

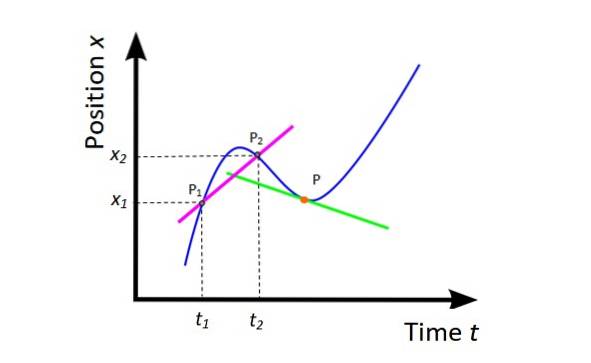
v_m = (X_Două - X₁) / (t_Două -t₁) = ΔX / Δt

Viteza medie este un vector ale cărui unități din sistemul internațional sunt metri / secundă (Domnișoară).

Viteza instantanee

Viteza medie se calculează luând un interval de timp măsurabil, dar nu raportează ce se întâmplă în acel interval. Pentru a cunoaște viteza în orice moment, trebuie să faceți intervalul de timp foarte mic, matematic este echivalent cu a face:

Δt → 0

Ecuația de mai sus este dată pentru viteza medie. În acest fel se obține viteza instantanee sau pur și simplu viteza:

Geometric, derivata poziției în raport cu timpul este panta liniei tangente la curbă X vs. t la un moment dat. În figura 4 punctul este portocaliu, iar linia tangentă este verde. Viteza instantanee în acel punct este panta acelei linii.

Viteză

Viteza este definită ca valoarea absolută sau modulul de viteză și este întotdeauna pozitivă (indicatoarele, drumurile și autostrăzile sunt întotdeauna pozitive, niciodată negative). Termenii „viteză” și „viteză” pot fi folosiți interschimbabil zilnic, dar în fizică este necesară distincția dintre vector și scalar.

v = ΙvΙ = v

Accelerație medie și accelerație instantanee

Viteza se poate schimba pe parcursul mișcării și realitatea este că se așteaptă să o facă. Există o magnitudine care cuantifică această schimbare: accelerația. Dacă observăm că viteza este schimbarea poziției față de timp, accelerația este schimbarea vitezei față de timp.

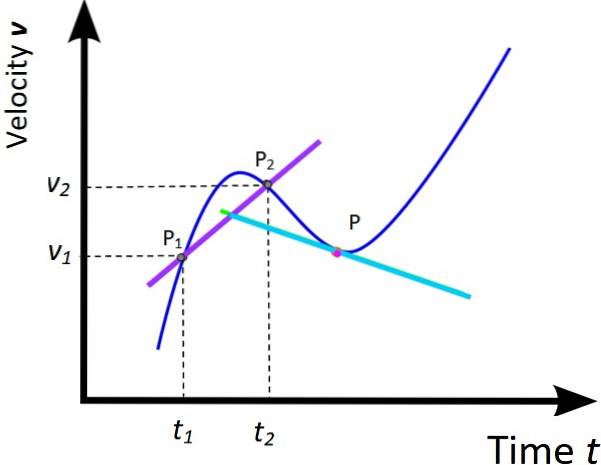
Tratamentul dat graficului X vs. t din cele două secțiuni anterioare pot fi extinse la graficul corespunzător al v vs. t. În consecință, o accelerație medie și o accelerație instantanee sunt definite ca:

la_m = (v_Două - v₁) / (t_Două -t₁) = Δv / Δt  (Panta liniei violete)

În mișcarea unidimensională, vectorii, prin convenție, au semne pozitive sau negative, în funcție de faptul că merg într-un fel sau altul. Când accelerația are aceeași direcție ca viteza, aceasta își mărește magnitudinea, dar atunci când are direcția opusă și viteza scade magnitudinea. Se spune apoi că mișcarea este întârziată.

Tipuri

Clasificarea mișcărilor rectilinii, în general, se bazează pe:

- Dacă accelerația este constantă sau nu.

- Mișcarea se desfășoară de-a lungul unei linii orizontale sau verticale.

Mișcare cu accelerație constantă

Când accelerația este constantă, accelerația medie la_m este egal cu accelerarea instantanee la și există două opțiuni:

- Că accelerația este egală cu 0, caz în care viteza este constantă și există o Mișcare Rectiliniară Uniformă sau MRU.

- Accelerație constantă, alta decât 0, în care viteza crește sau scade liniar cu timpul (mișcarea rectilinie cu variație uniformă sau MRUV):

Unde v_F  Da t_F sunt viteza finală și, respectiv, timpul și v_sau Da t_sau sunt viteza și timpul inițial. da t_sau = 0, Rezolvând viteza finală avem deja ecuația familiară pentru viteza finală:

v_F = v_sau + la

Următoarele ecuații sunt valabile și pentru această mișcare:

- Poziția în funcție de timp: x = x_sau + v_{sau .}t + ½ la^Două

- Viteza în funcție de poziție: v_F^Două = v_sau^Două + Al doileaX  (Cu Δx = x - x_sau)

Mișcări orizontale și mișcări verticale

Mișcările orizontale sunt cele care au loc de-a lungul axei orizontale sau axa x, în timp ce mișcările verticale o fac de-a lungul axei y. Mișcările verticale sub acțiunea gravitației sunt cele mai frecvente și interesante.

În ecuațiile anterioare, luăm a = g = 9,8 m / s^Două direcționat vertical în jos, o direcție care este aproape întotdeauna aleasă cu semn negativ.

În acest fel, v_F = v_sau + la Se transformă în v_F = v_sau - gt iar dacă viteza inițială este 0 deoarece obiectul a fost scăpat liber, se simplifică și mai mult la v_F = - gt. Atâta timp cât rezistența la aer nu este luată în considerare, desigur.

Exemple lucrate

Exemplul 1

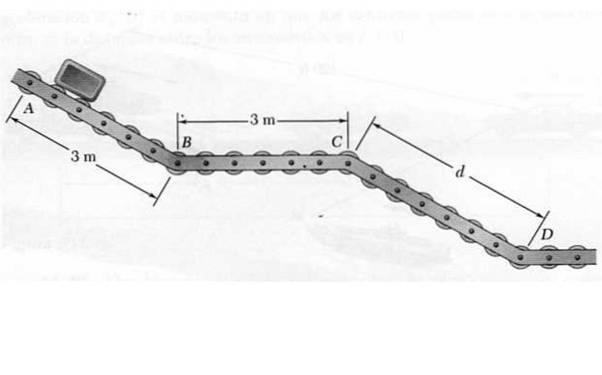
În punctul A se eliberează un mic pachet pentru a se deplasa de-a lungul transportorului cu roți glisante ABCD prezentate în figură. În timp ce coborâți pantele AB și CD, pachetul are o accelerație constantă de 4,8 m / s^Două, în timp ce în secțiunea orizontală BC menține viteza constantă.

Știind că viteza cu care pachetul ajunge la D este de 7,2 m / s, determinați:

a) Distanța dintre C și D.

b) Timpul necesar pachetului pentru a ajunge la final.

Soluţie

Mișcarea ambalajului se efectuează în cele trei secțiuni rectilinii afișate și pentru a calcula ceea ce se solicită, viteza este necesară în punctele B, C și D. Să analizăm fiecare secțiune separat:

Secțiunea AB

Deoarece timpul nu este disponibil în această secțiune, acesta va fi folosit v_F^Două = v_sau^Două + Al 2-leaX  cu vo = 0:

v_F^Două = 2a.Δx → v_F^Două= 2,8 4,8 m / s^Două . 3 m = 28,8 m^Două/ s^Două → v_F  = 5,37 m / s = v_B

Timpul necesar pachetului pentru a parcurge secțiunea AB este:

t_AB = (v_F - v_sau) / a = 5,37 m / s / 4,8 m / s^Două = 1,19 s

Secțiunea BC

Prin urmare, viteza din secțiunea BC este constantă v_B = v_C = 5,37 m / s. Timpul necesar pachetului pentru a parcurge această secțiune este:

t_Î.Hr. = distanță _Î.Hr.  / v_B = 3 m / 5,37 m / s = 0,56 s

Secțiunea CD

Viteza inițială a acestei secțiuni este v_C = 5,37 m / s, viteza finală este v_D = 7,2 m / s, cu v_D^Două  = v_C^Două + 2. a. d valoarea lui este ștearsă d:

d = (v_D^Două  - v_C^Două) /2.a = (7.2^Două  - 5.37^Două)/Două X 4,8 m = 2,4 m

Timpul este calculat ca:

t_{CD =} (v_D  - v_C) / a = (7,2 - 5,37) / 4,8 s = 0,38 s.

Răspunsurile la întrebările puse sunt:

a) d = 2,4 m

b) Timpul de călătorie este t_AB + t_Î.Hr. + t_CD = 1,19 s +0,56 s +0,38 s = 2,13 s.

Exemplul 2

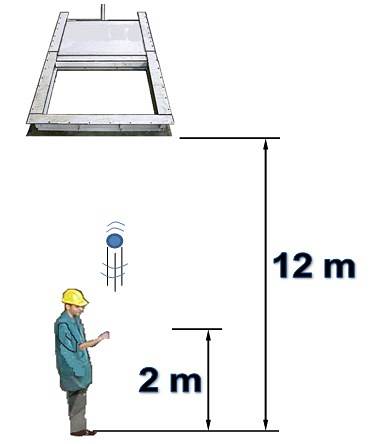
O persoană se află sub o poartă orizontală care este inițial deschisă și înaltă de 12 m. Persoana aruncă vertical un obiect spre poartă cu o viteză de 15 m / s.

Se știe că poarta se închide la 1,5 secunde după ce persoana a aruncat obiectul de la o înălțime de 2 metri. Rezistența la aer nu va fi luată în considerare. Răspundeți la următoarele întrebări, justificând:

a) Poate obiectul să treacă prin poartă înainte de a se închide?

b) Obiectul se va ciocni vreodată cu poarta închisă? Dacă da, când o face?

Raspunde la)

Există 10 metri între poziția inițială a mingii și poartă. Este o aruncare verticală în sus, în care această direcție este luată ca pozitivă.

Puteți afla viteza necesară pentru a atinge această înălțime, cu acest rezultat se calculează timpul necesar pentru ao face și se compară cu timpul de închidere a porții, care este de 1,5 secunde:

v_F ^Două= v_sau ^Două- 2 g. Δși → v_F = (15^Două - Două X 9.8 X10)^1/2 m = 5,39 m / s

t = (v_F - v_sau) / g = (5,39 - 15) / (-9,8) s = 0,98 s

Deoarece acest timp este mai mic de 1,5 secunde, se concluzionează că obiectul poate trece prin poartă cel puțin o dată.

Răspuns b)

Știm deja că obiectul reușește să treacă prin poartă în timp ce urcă, să vedem dacă îi dă șansa să treacă din nou la coborâre. Viteza, la atingerea înălțimii porții, are aceeași magnitudine ca atunci când merge în sus, dar în direcția opusă. Prin urmare, lucrăm cu -5,39 m / s și timpul necesar pentru a ajunge la această situație este:

t = (v_F - v_sau) / g = (-5,39 - 15) / (-9,8) s = 2,08 s

Deoarece poarta rămâne deschisă doar 1,5 secunde, este evident că nu are timp să treacă din nou înainte de a se închide, deoarece o găsește închisă. Răspunsul este: obiectul dacă se ciocnește cu trapa închisă după 2,08 secunde după ce a fost aruncat, când acesta este deja descendent.

Referințe

1. Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB) .69-116.
2. Giancoli, D. Fizică. (2006). Principii cu aplicații. 6^a Ediție. Prentice Hall. 22-25.
3. Kirkpatrick, L. 2007. Fizica: O privire asupra lumii. 6^ta Ediție scurtată. Cengage Learning. 23 - 27.
4. Resnick, R. (1999). Fizic. Volumul 1. Ediția a treia în limba spaniolă. Mexic. Compañía Editorial Continental S.A. de C.V. 21-22.
5. Rex, A. (2011). Bazele fizicii. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14^a. Ed. Volumul 1. 50 - 53.
7. Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7^ma. Ediție. Mexic. Editorii de învățare Cengage. 23-25.
8. Serway, R., Vulle, C. (2011). Bazele fizicii. 9^{n / A} Ed. Cengage Learning. 43 - 55.
9. Wilson, J. (2011). Fizică 10. Educația Pearson. 133 - 149.