Caracteristici de mișcare rectilinie accelerată uniform, formule

mișcare rectilinie accelerată uniform Este una care rulează de-a lungul unei linii drepte și în care mobilul își mărește sau scade viteza la o rată constantă. Această rată este magnitudinea care descrie viteza cu care se schimbă viteza și se numește accelerare.

În cazul mișcării rectilinii uniform accelerate sau variate (MRUV), accelerația constantă este responsabilă pentru modificarea magnitudinii vitezei. În alte tipuri de mișcare, accelerația este, de asemenea, capabilă să schimbe direcția și sensul vitezei, sau chiar doar să schimbe direcția, ca în mișcarea circulară uniformă..

Deoarece accelerația reprezintă schimbarea vitezei în timp, unitățile sale din sistemul internațional sunt m / s^Două (metri peste secunde pătrate). La fel ca viteza, accelerației i se poate atribui un semn pozitiv sau negativ, în funcție de creșterea sau scăderea vitezei..

O accelerație de +3 m / s^Două înseamnă că pentru fiecare secundă care trece, viteza telefonului mobil crește cu 3 m / s. Dacă la începutul mișcării (la t = 0) viteza mobilului a fost de +1 m / s, atunci după o secundă va fi de 4 m / s și după 2 secunde va fi de 7 m / s.

În mișcare rectilinie uniform variată, se iau în considerare variațiile de viteză pe care obiectele în mișcare le experimentează zilnic. Acesta este un model mai realist decât mișcarea rectilinie uniformă. Chiar și așa, este încă destul de limitat, deoarece restricționează telefonul mobil să circule doar pe o linie dreaptă.

Indice articol

• 1 Caracteristici
  • 1.1 Distanța parcursă față de v vs. grafic t
• 2 Formule și ecuații
• 3 exerciții rezolvate
  • 3.1 -Exercițiu rezolvat 1
  • 3.2 - Exercițiu rezolvat 2
• 4 Aplicații
• 5 Referințe

Caracteristici

Acestea sunt principalele caracteristici ale mișcării rectilinii uniform accelerate:

-Mișcarea rulează întotdeauna de-a lungul unei linii drepte.

-Accelerația mobilului este constantă, atât în ​​mărime, cât și în direcție și sens.

-Viteza mobilului crește (sau scade) liniar.

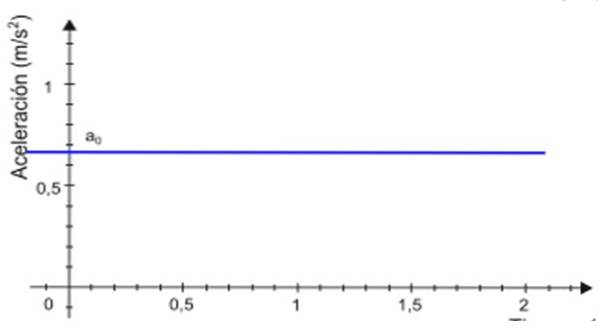
-De la accelerare la rămâne constantă în timp t, graficul mărimii sale în funcție de timp este o linie dreaptă. În exemplul prezentat în figura 2, linia este colorată în albastru și valoarea accelerației este citită pe axa verticală, aproximativ +0,68 m / s^Două.

-Graficul vitezei v despre t este o linie dreaptă (în verde în figura 3), a cărei pantă este egală cu accelerația mobilului. În exemplu, panta este pozitivă.

-Tăierea cu axa verticală indică viteza inițială, în acest caz este de 0,4 m / s.

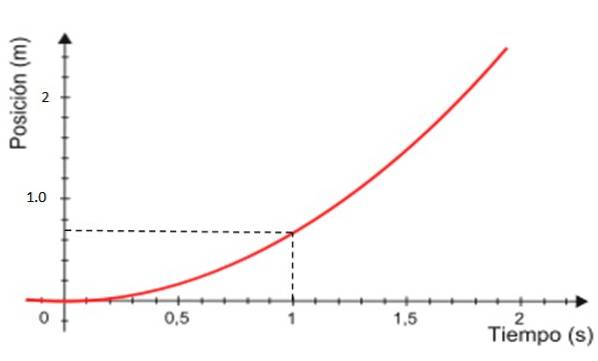
-În cele din urmă, graficul poziției x versus timp este curba prezentată în roșu în figura 4, care este întotdeauna o parabolă.

Distanța parcursă de la v vs. grafic. t

Având graficul v vs. t, calcularea distanței parcurse de mobil este foarte ușoară. Distanța parcursă este egală cu aria de sub linie care se află în intervalul de timp dorit.

În exemplul prezentat, să presupunem că doriți să cunoașteți distanța parcursă de mobil între 0 și 1 secundă. Folosind acest grafic, vezi Figura 5.

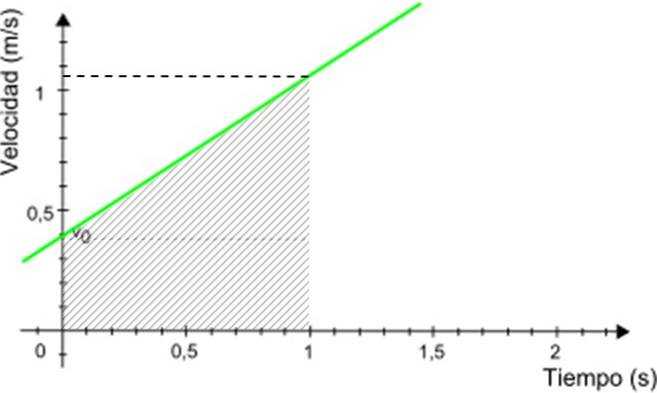
Distanța căutată este echivalentă numeric cu aria trapezului umbrit în figura 3. Aria trapezului este dată de: (bază majoră + bază minoră) x înălțime / 2

Distanța parcursă = (0,4 + 1,05) x 1/2 m = 0,725 m

De asemenea, este posibil să împărțiți zona umbrită într-un triunghi și un dreptunghi, să calculați ariile corespunzătoare și să le adăugați împreună. Distanța parcursă este pozitivă, chiar dacă particula merge spre dreapta sau spre stânga.

Formule și ecuații

Atât accelerația medie, cât și accelerația instantanee au aceeași valoare în MRUV, prin urmare:

-Accelerare: la = constant

Când accelerația este egală cu 0 mișcarea este rectilinie uniformă, deoarece viteza ar fi constantă în acest caz. Semnul la Poate fi pozitiv sau negativ.

Deoarece accelerația este panta liniei v față de t, ecuația v (t) este:

-Viteza în funcție de timp: v (t) = v_sau + la

Unde v_sau este valoarea vitezei inițiale a telefonului mobil

-Poziția în funcție de timp: x (t) = x_sau + v_sau t + ½at^Două 

Când nu aveți timp, dar în schimb aveți viteze și deplasări, există o ecuație foarte utilă care se obține rezolvând timpul de v (t) = v_sau + la și înlocuind-o în ultima ecuație. Este despre:

-Ecuație care nu conține timp: v^Două = v_sau^Două +2.a.ΔX

Exerciții rezolvate

Când rezolvați un exercițiu cinematic, este important să vă asigurați că situația este adaptată la modelul care urmează să fie utilizat. De exemplu, ecuațiile mișcării rectilinii uniforme nu sunt valabile pentru mișcarea accelerată.

Și cele ale mișcării accelerate nu sunt valabile, de exemplu, pentru o mișcare circulară sau curbiliniară. Primul dintre aceste exerciții rezolvate mai jos combină două telefoane mobile cu mișcări diferite. Pentru a o rezolva corect, este necesar să mergeți la modelul de mișcare adecvat.

-Exercițiu rezolvat 1

Pentru a afla adâncimea unei fântâni, un copil aruncă o monedă și, în același timp, își activează cronometrul, care se oprește imediat după ce a auzit moneda lovind apa. Citirea sa a fost de 2,5 secunde. Știind că viteza sunetului în aer este de 340 m / s, calculați adâncimea puțului.

Soluţie

Fi h adâncimea puțului. Moneda parcurge această distanță în cădere liberă, o mișcare verticală uniform variată, cu viteza inițială 0, pe măsură ce moneda este scăzută și o accelerație constantă în jos egală cu 9,8 m / s^Două. Ia-ți timp t_m în a face acest lucru.

Odată ce moneda lovește apa, sunetul cauzat de clic se deplasează în sus până la urechea copilului, care oprește cronometrul la auzul acestuia. Nu există niciun motiv să credem că viteza sunetului se schimbă pe măsură ce se ridică în puț, astfel încât mișcarea sunetului este uniformă rectilinie. Sunetul durează puțin t_s pentru a ajunge la copil.

Ecuația mișcării monedei:

h = ½.g.t_m ^Două = 4,9 t_m ^Două

Unde au fost înlocuite X Da la a ecuației pentru poziția dată în secțiunea anterioară, de h Da g.

Ecuația mișcării pentru sunet:

h = v_s . t_s = 340 t_s

Este vorba despre ecuația familiară distanță = viteză x timp. Cu aceste două ecuații avem trei necunoscute: h, tm și ts. Pentru momentele în care există o relație, se știe că totul durează 2,5 secunde pentru a se întâmpla, prin urmare:

t_m + t_s = 2,5 s

Echivalarea ambelor ecuații:

4,9 t_m ^Două = 340 t_s

Ștergerea uneia dintre situații și înlocuirea:

4,9 t_m ^Două= 340. (2,5 - t_m)

Dezvoltând termenul potrivit și transpunând termenii, obținem:

4,9 t_m ^Două+340 t_m - 850 = 0

Aceasta este o ecuație pătratică cu două soluții: 2.416 și -71.8. Se alege soluția pozitivă, care este cea care are sens, deoarece timpul nu poate fi negativ și în orice caz trebuie să fie mai mic de 2,5 secunde. Pentru acest timp se obține prin înlocuirea adâncimii puțului:

4,9 t_m ^Două= 4,9 x 2,416^Două m = 28,6 m

-Exercițiu rezolvat 2

O mașină care circulă cu 90 km / h se apropie de o stradă transversală cu semafor. Când se află la 70 m de acolo, se aprinde lumina galbenă, care durează 4 secunde. Distanța dintre semafor și colțul următor este de 50 m.

Șoferul are aceste două opțiuni: a) frână la - 4 m / s^Două sau b) accelerați la + 2 m / s^Două. Care dintre cele două opțiuni îi permite șoferului să oprească sau să traverseze întregul bulevard înainte ca lumina să devină roșie?

Soluţie

Poziția de plecare a șoferului este x = 0 exact când vede lumina galbenă aprinsă. Este important să convertiți unitățile în mod corespunzător: 90 km / h este egal cu 25 m / s.

Conform opțiunii a), în cele 4 secunde care durează lumina galbenă, șoferul călătorește:

x (t) = v_sau t + ½at^Două= 25,4 -½. (- 4) .4^Douăm = 68 m (Se oprește cu 2 metri înainte de semafor)

Analizând opțiunea b) avem:

x (t) = v_sau t + ½at^Două= 25.t + ½.2.t^Două

În timp ce lumina galbenă durează, șoferul călătorește în acest fel:

x = 25,4 + ½.2,4^Douăm = 116 m

Dar 116 m este mai mică decât distanța disponibilă pentru a ajunge la următorul colț, care este de 70 + 50 m = 120 m, prin urmare el nu poate traversa întreaga stradă înainte de aprinderea luminii roșii. Acțiunea recomandată este de a frâna și a sta la 2 metri de semafor.

Aplicații

Oamenii experimentează efectele accelerației zilnic: atunci când călătoresc cu mașina sau autobuzul, deoarece acestea trebuie să frâneze și să accelereze continuu pentru a adapta viteza la obstacolele de pe drum. Accelerarea este, de asemenea, experimentată atunci când urcați sau coborâți într-un lift.

Parcurile de distracții sunt locuri în care oamenii plătesc pentru a experimenta efectele accelerației și a se distra.

În natură, mișcarea rectilinie uniform variată este observată atunci când un obiect este lăsat liber sau când este aruncat vertical în sus și așteptat să se întoarcă la sol. Dacă rezistența aerului este neglijată, valoarea accelerației este cea a gravitației: 9,8 m / s2.

Referințe

1. Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill. 40-45.
2. Figueroa, D. Seria de fizică pentru științe și inginerie. Volumul 3. Ediție. Cinematică. 69-85.
3. Giancoli, D. Fizica: Principii cu aplicații. 6^a. Sala Ed Prentice. 19-36.
4. Hewitt, Paul. 2012. Științe fizice conceptuale. 5^a. Ed. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Fizica: O privire asupra lumii. 6^ta Ediție scurtată. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fizică 10. Pearson Education. 116-119