Mișcare relativă într-o dimensiune, în două dimensiuni, exerciții

mișcare relativă a unei particule sau a unui obiect este cea care se observă cu privire la un anumit punct de referință ales de observator, care poate fi fix sau în mișcare. Viteza se referă întotdeauna la un sistem de coordonate utilizat pentru a-l descrie.

De exemplu, pasagerul unei mașini în mișcare și care călătorește confortabil adormit pe scaunul său este odihnit față de șofer, dar nu pentru un observator care stă pe trotuar și vede mașina trecând..

Apoi mișcarea este întotdeauna relativă, dar se întâmplă ca, în general, să se aleagă sistemul de coordonate sau de referință care își are originea în Pământ sau sol, un loc considerat staționar. În acest fel, preocuparea se concentrează pe descrierea mișcării obiectului în studiu..

Este posibil să descrieți viteza copilotului care dorm în comparație cu un pasager care călătorește într-o altă mașină? Raspunsul este da. Există libertatea de a alege valoarea lui (x_sau, Da_sau, z_sau): originea sistemului de referință. Selecția este arbitrară și depinde de preferința observatorului, precum și de ușurința pe care o oferă pentru rezolvarea problemei..

Indice articol

• 1 Mișcare relativă într-o singură dimensiune
  • 1.1 - Exemplu lucrat 1
• 2 Mișcare relativă în două și trei dimensiuni
  • 2.1 - Exercițiu rezolvat 2 
  • 2.2 - Exercițiu rezolvat 3
• 3 Referințe

Mișcare relativă într-o singură dimensiune

Când mișcarea are loc de-a lungul unei linii drepte, telefoanele mobile au viteze în aceeași direcție sau în direcția opusă, ambele văzute de un observator care stă pe Pământ (T). Observatorul se mișcă în ceea ce privește telefoanele mobile? Da, cu aceeași viteză pe care o poartă, dar în direcția opusă.

Cum se mișcă un mobil față de celălalt? Pentru a afla, viteza se adaugă vectorial.

-Exemplu lucrat 1

Referindu-vă la figura prezentată, indicați viteza relativă a mașinii 1 față de mașina 2 în fiecare situație.

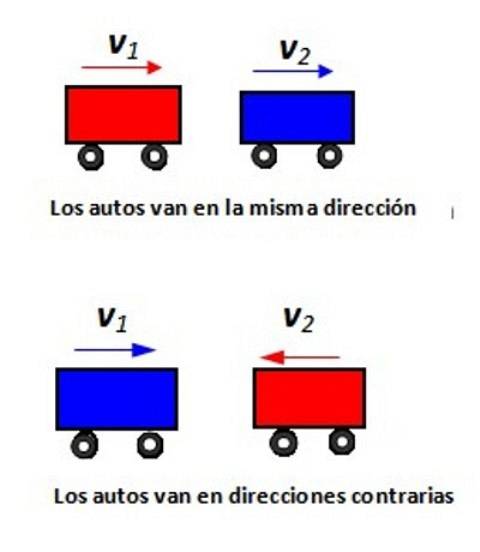
Soluţie

Vom atribui un semn pozitiv vitezei la dreapta și un semn negativ la stânga. Dacă un mobil merge la dreapta la 80 km / h, un pasager de pe acest mobil vede observatorul de pe Pământ deplasându-se la - 80 km / h.

Să presupunem că totul se întâmplă de-a lungul axei x. În figura următoare, mașina roșie se deplasează la +100 km / h (văzută din T) și este pe cale să treacă peste mașina albastră care călătorește cu +80 km / h (văzută și din T). Cât de repede se apropie un pasager din mașina albastră de mașina roșie?

Etichetele sunt: v _1/2 viteza mașinii 1 față de mașina 2, v_{1 / T} viteza mașinii față de T, v_{T / 2} viteza lui T față de 2. Adăugarea vectorului:

v_1/2 = v_{1 / T} + v_{T / 2} = (+100 km / h - 80 km / h) X= 20 km / h X

Ne putem descurca fără notația vectorială. Observați indicele: înmulțind cele două din dreapta ar trebui să obțineți cel din stânga.

Și când merg în sens invers? Acum v_{1 / T} = + 80 km / h și v_{2 / T} = -100 km / h, deci v_{T / 2} = + 100 km / h. Pasagerul mașinii albastre va vedea că mașina roșie se apropie:

v_{1/2 =} v_{1 / T} + v_{T / 2} = +80 km / h +100 km / h = 180 km / h

Mișcare relativă în două și trei dimensiuni

În schema următoare, r este poziția planului văzută din sistem X și Z, r'este poziția din sistem X și Z ' Da R este poziția sistemului cu o primă față de sistemul fără primă. Cei trei vectori formează un triunghi în care R + r'= r, Prin urmare r'= r - R.

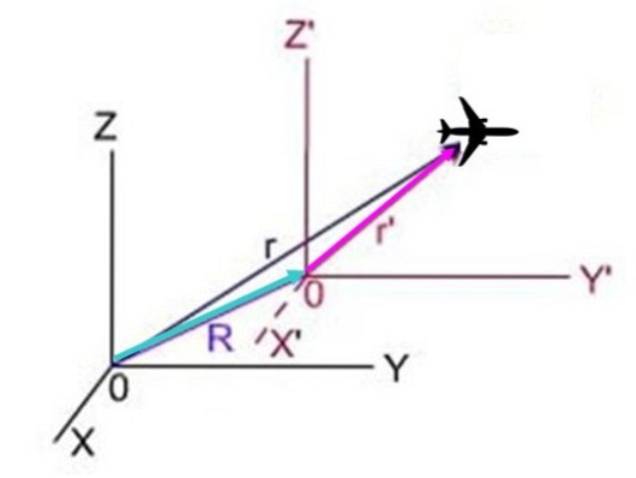
Deoarece derivata în ceea ce privește timpul poziției este tocmai viteza, rezultă:

v'= v - sau

În această ecuație v'este viteza avionului față de sistem X și Z ', v este viteza față de sistem X și Z Da sau este viteza constantă a sistemului prim în raport cu sistemul neprimat.

-Exercițiu rezolvat 2 

Un avion se îndreaptă spre nord, cu viteza de 240 km / h. Deodată vântul începe să sufle de la vest la est cu o viteză de 120 km / în funcție de pământ.

Găsiți: a) Viteza avionului față de sol, b) Abaterea experimentată de pilot c) Corecția pe care trebuie să o facă pilotul pentru a putea viza direct spre nord și noua viteză față de sol, odată corectarea a fost făcută.

Soluţie

a) Există următoarele elemente: planul (A), solul (T) și vântul (V).

În sistemul de coordonate în care nordul este direcția + y, iar direcția vest-est este + x, avem viteza dată și eticheta respectivă (indicele):

v _AV = 240 km / h (+Da); v _{V / T} = 120 km / h (+X); v _{A / T} = ?

Suma vectorială adecvată este:

v _{A / T} = v _AV + v _{V / T} = 240 km / h (+Da) + 120 km / h (+X)

Mărimea acestui vector este: v _{A / T} = (240 ^Două+ 120^Două)^1/2 km / h = 268,3 km / h

b) θ = arctg (v _AV / v _{V / T}) = arctg (240/120) = 63,4º nord de est sau 26,6º nord-est.

c) Pentru a continua spre nord cu acest vânt, va trebui să îndreptați arcul aeronavei spre nord-vest, astfel încât vântul să vă împingă direct spre nord. În acest caz, viteza avionului văzută de la sol va fi în direcția + y, în timp ce viteza avionului față de vânt va fi nord-vest (nu trebuie neapărat să fie 26,6º).

Prin teorema lui Pitagora:

v _{A / T} = (240 ^Două- 120^Două)^1/2 km / h = 207,8 km / h

α = arctg (v _{V / T} / v _{A / T} ) = arctg (120 / 207.8) = 30º Nord-Vest

-Exercițiu rezolvat 3

O persoană durează 2 minute să meargă pe o scară rulantă staționară. Dacă scara funcționează, persoana durează 1 minut să coboare în timp ce stă pe loc. Cât durează persoana să coboare cu scara în funcțiune?

Soluţie

Există trei elemente de luat în considerare: persoana (P), scara (E) și solul (S), ale căror viteze relative sunt:

v_{P / E} : viteza persoanei în raport cu scara; v_ESTE: viteza scării în raport cu solul; v_{P / S}: viteza persoanei față de sol.

După cum este văzut de la sol de un observator fix, persoana care coboară pe scară (E) are o viteză v _{P / S} dat de:

v _{P / S} = v_{P / E} + v_ESTE

Direcția pozitivă coboară pe scară. Fi t  timpul necesar pentru a coborî și L distanţă. Mărimea vitezei persoanei v _{P / S} este:

v_{P / S} = L / t

t₁ este timpul necesar pentru a coborî cu scara oprită: v _{P / E} = L / t₁

Si t_Două cel care te doboară încă pe scara în mișcare: v _ESTE = L / t_Două

Combinând expresiile:

L / t = L / t₁ + L / t_Două

Înlocuirea valorilor numerice și rezolvarea t:

1 / t = 1 / t₁ + 1 / t_Două = 1/2 + 1/1 = 1,5

Deci t = 1 / 1,5 minute = 40 secunde.

Referințe

1. Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Seria de fizică pentru științe și inginerie. Volumul 3. Ediție. Cinematică. 199-232.
3. Giancoli, D. 2006. Fizică: principii cu aplicații. 6^a. Ed. Prentice Hall. 62-64.
4. Mișcare relativă. Recuperat de la: courses.lumenlearning.com
5. Wilson, J. 2011. Fizică 10. Pearson Education. 166-168.