
Definiția și caracteristicile unghiului nul, exemple, exerciții
unghiul nul Este una a cărei măsură este 0, atât în grade, cât și în radiani sau un alt sistem de măsurare a unghiului. Prin urmare, îi lipsește lățimea sau deschiderea, cum ar fi cea formată între două linii paralele..
Deși definiția sa sună suficient de simplă, unghiul nul este foarte util în multe aplicații de fizică și inginerie, precum și în navigație și proiectare..
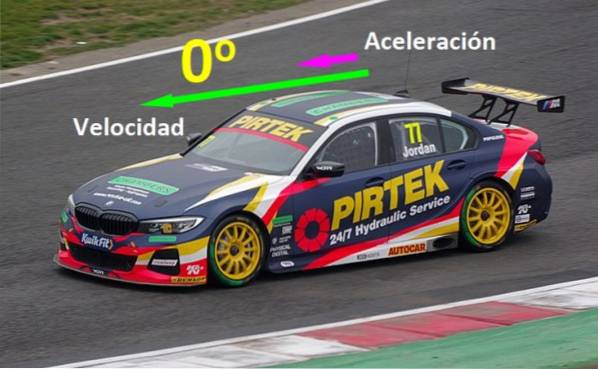
Există cantități fizice care trebuie aliniate în paralel pentru a obține anumite efecte: dacă o mașină se deplasează în linie dreaptă pe o autostradă și introduceți vectorul său de viteză v și vectorul său de accelerație la există 0º, mașina se mișcă din ce în ce mai repede, dar dacă mașina frânează, accelerația sa este opusă vitezei sale (vezi figura 1).
Figura următoare prezintă diferite tipuri de unghi, inclusiv unghiul nul spre dreapta. După cum se poate observa, unghiul 0º nu are lățime sau deschidere..

Indice articol
- 1 Exemple de unghiuri nule
- 1.1 - Efectele unghiului nul asupra magnitudinilor fizice
- 2 Exerciții
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Referințe
Exemple de unghiuri nule
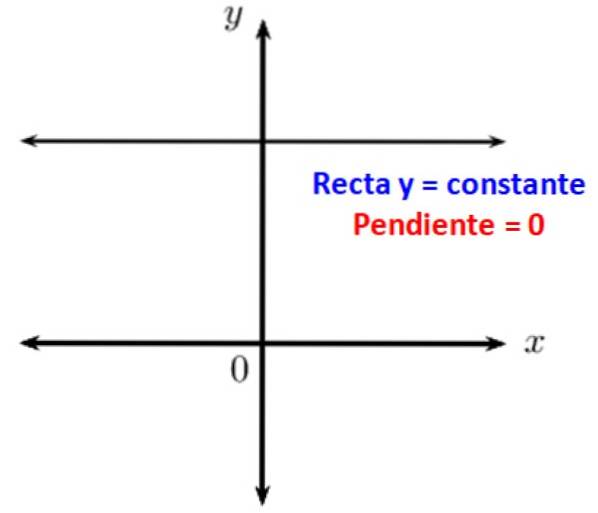
Se știe că liniile paralele formează un unghi zero între ele. Când aveți o linie orizontală, aceasta este paralelă cu axa x a sistemului de coordonate carteziene, prin urmare, înclinația sa față de ea este 0. Cu alte cuvinte, liniile orizontale au o pantă zero.
De asemenea, raporturile trigonometrice ale unghiului nul sunt 0, 1 sau infinit. Prin urmare unghiul nul este prezent în multe situații fizice care implică operații cu vectori. Aceste motive sunt:
-sin 0º = 0
-cos 0º = 1
-tg 0º = 0
-sec 0º = 1
-cosec 0º → ∞
-ctg 0º → ∞
Și vor fi utile pentru a analiza câteva exemple de situații în care prezența unghiului nul joacă un rol fundamental:
- Efectele unghiului nul asupra mărimilor fizice
Adăugare vectorială
Când doi vectori sunt paraleli, unghiul dintre ei este zero, așa cum se vede în Figura 4a de mai sus. În acest caz, suma ambelor se realizează prin plasarea una după alta, iar magnitudinea vectorului sumă este suma mărimilor addendelor (figura 4b).

Când doi vectori sunt paraleli, unghiul dintre ei este zero, așa cum se vede în Figura 4a de mai sus. În acest caz, suma ambelor se realizează prin plasarea una după alta, iar magnitudinea vectorului sumă este suma mărimilor addendelor (figura 4b)
Cuplul sau cuplul
Cuplul sau cuplul determină rotația unui corp. Depinde de amploarea forței aplicate și de modul în care este aplicată. Un exemplu foarte reprezentativ este cheia din figură.
Pentru a obține cel mai bun efect de rotire, forța este aplicată perpendicular pe mânerul cheii, fie în sus, fie în jos, dar nu se așteaptă nicio rotație dacă forța este paralelă cu mânerul..
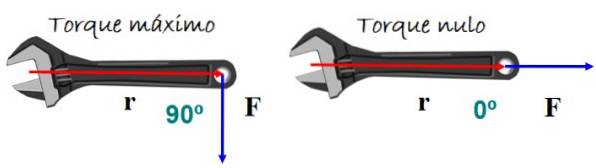
Cuplu matematic τ este definit ca produsul încrucișat sau produsul încrucișat între vectori r (vectorul de poziție) și F (vectorul de forță) din figura 5:
τ = r X F
Mărimea cuplului este:
τ = r F sin θ
Unde θ este unghiul dintre r Da F. Când sin θ = 0 cuplul este zero, în acest caz θ = 0º (sau, de asemenea, 180º).
Fluxul câmpului electric
Fluxul câmpului electric este o magnitudine scalară care depinde de intensitatea câmpului electric, precum și de orientarea suprafeței prin care trece..
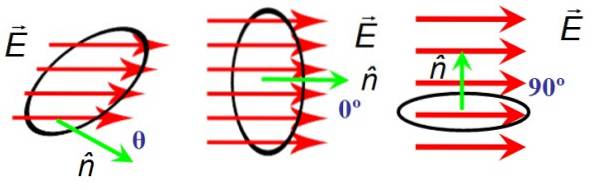
În figura 6 există o suprafață circulară a zonei A prin care trec liniile câmpului electric ȘI. Orientarea suprafeței este dată de vectorul normal n. În stânga câmpul și vectorul normal formează un unghi acut arbitrar θ, în centru formează un unghi nul între ele, iar în dreapta sunt perpendiculare.
Cand ȘI Da n sunt perpendiculare, liniile de câmp nu traversează suprafața și, prin urmare, fluxul este zero, în timp ce când unghiul dintre ȘI Da n este nul, liniile traversează complet suprafața.
Notând fluxul de câmp electric prin litera greacă Φ (citiți „fi”), definiția sa pentru un câmp uniform ca în figură, arată astfel:
Φ = ȘI•nLA
Punctul din mijlocul ambilor vectori denotă produsul punct sau produsul punct, care este definit alternativ după cum urmează:
Φ = ȘI•nA = EAcosθ
Grăsimile și săgețile de deasupra literei sunt resurse pentru a face diferența între un vector și magnitudinea acestuia, care este notată cu litere normale. Deoarece cos 0 = 1, fluxul este maxim când ȘI Da n sunt paralele.
Instruire
- Exercitiul 1
Două forțe P Da Î acționează simultan asupra unui obiect punct X, ambele forțe formează inițial un unghi θ între ele. Ce se întâmplă cu magnitudinea forței rezultate atunci când θ scade la zero?
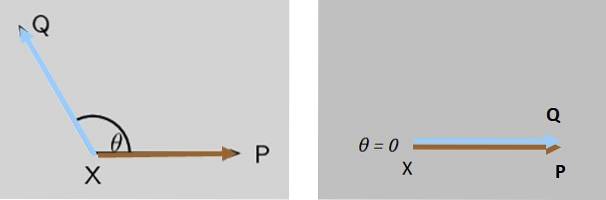
Soluţie
Mărimea forței rezultate Î + P crește treptat până când este maxim când Î Da P sunt total paralele (figura 7 dreapta).
- Exercițiul 2
Indicați dacă unghiul nul este o soluție a următoarei ecuații trigonometrice:
cos 2x = 1 + 4 sin x
Soluţie
O ecuație trigonometrică este una în care necunoscutul face parte din argumentul unui raport trigonometric. Pentru a rezolva ecuația propusă, este convenabil să utilizați formula pentru cosinusul unghiului dublu:
cos 2x = cosDouă x - păcatDouă X
Pentru că în acest fel, argumentul din partea stângă devine X in loc de 2x. Atunci:
cosDouă x - păcatDouă x = 1 + 4sin x
Pe de altă parte, cosDouă x + păcatDouă x = 1, deci:
cosDouă x - păcatDouă x = cosDouă x + păcatDouă x + 4sen x
Termenul cosDouă x este anulat și rămâne:
- senDouă x = păcatDouă x + 4sen x → - 2senDouă x - 4senx = 0 → 2senDouă x + 4senx = 0
Acum se face următoarea modificare a variabilei: sinx = u și ecuația devine:
2uDouă + 4u = 0
2u (u + 4) = 0
A căror soluție este: u = 0 și u = -4. Revenind la schimbare am avea două posibilități: sin x = 0 și sinx = -4. Această ultimă soluție nu este viabilă, deoarece sinusul oricărui unghi este între -1 și 1, deci rămânem cu prima alternativă:
sin x = 0
Prin urmare, x = 0º este o soluție, dar funcționează și orice unghi al cărui sinus este 0, care poate fi și 180º (π radieni), 360º (2 π radiani) și negativele respective.
Cea mai generală soluție a ecuației trigonometrice este: x = kπ unde k = 0, ± 1, ± 2, ± 3,…. k un număr întreg.
Referințe
- Baldor, A. 2004. Geometria planului și spațiului cu trigonometrie. Publicaciones Cultural S.A. de C.V. Mexic.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 3. Sisteme de particule. Editat de Douglas Figueroa (USB).
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 5. Interacțiunea electrică. Editat de Douglas Figueroa (USB).
- OnlineMathLearning. Tipuri de unghiuri. Recuperat de pe: onlinemathlearning.com.
- Zill, D. 2012. Algebră, trigonometrie și geometrie analitică. McGraw Hill Interamericana.



Nimeni nu a comentat acest articol încă.