
Proprietăți de numere complexe, exemple, operații
numere complexe sunt mulțimea numerică care include numerele reale și toate rădăcinile polinoamelor, inclusiv rădăcinile pare ale numerelor negative. Aceste rădăcini nu există în mulțimea numerelor reale, dar în numerele complexe există soluția.
Un număr complex constă dintr-o parte reală și o parte numită „imaginar”. Partea reală se numește la, de exemplu, și partea imaginară ib, cu la Da b numere reale și „i” ca. unitate imaginară. În acest fel, numărul complex ia forma:
z = a + ib

Exemple de numere complexe sunt 2 - 3i, -πi, 1 + (1/2) i. Dar, înainte de a opera cu ei, să vedem de unde își are originea unitatea imaginară eu, având în vedere această ecuație pătratică:
XDouă - 10x + 34 = 0
În care a = 1, b = -10 și c = 34.
Când aplicăm formula de rezolvare pentru a determina soluția, găsim următoarele:

Cum se determină valoarea lui √-36? Nu există un număr real care să aibă drept rezultat pătrat o cantitate negativă. Apoi se concluzionează că această ecuație nu are soluții reale.
Cu toate acestea, putem scrie acest lucru:
√-36 = √-6Două = √6Două (-1) = 6√-1
Dacă definim o anumită valoare X astfel încât:
XDouă = -1
Atunci:
x = ± √-1
Și ecuația de mai sus ar avea o soluție. Prin urmare, unitatea imaginară a fost definită ca:
i = √-1
Așadar:
√-36 = 6i
Mulți matematicieni din antichitate au lucrat la rezolvarea unor probleme similare, în special Renașterea Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) și Raffaele Bombelli (1526-1572).
Ani mai târziu, René Descartes (1596-1650) a numit cantități precum √-36 în exemplul „imaginar”. Din acest motiv √-1 este cunoscut sub numele de unitate imaginară.
Indice articol
- 1 Proprietățile numerelor complexe
- 2 Reprezentarea numerelor complexe
- 2.1 - Forma binomială
- 2.2 - Forma polară
- 3 Exemple de numere complexe
- 4 Pentru ce sunt?
- 5 Operații cu numere complexe
- 5.1 - Exemplul 1
- 5.2 - Exemplul 2
- 6 Cerere
- 7 Referințe
Proprietățile numerelor complexe
-Mulțimea numerelor complexe este notată C și include numerele reale R și numerele imaginare Im. Seturile de numere sunt reprezentate într-o diagramă Venn, așa cum se arată în figura următoare:
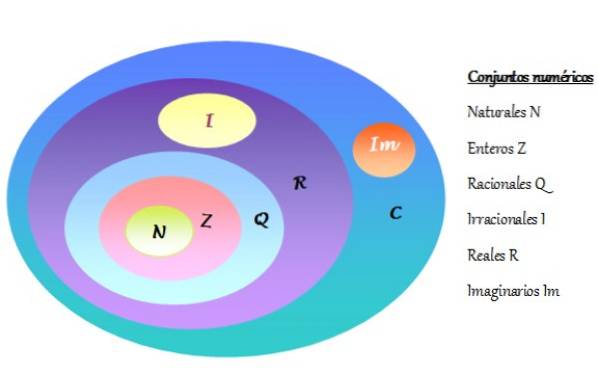
-Fiecare număr complex este format dintr-o parte reală și o parte imaginară.
-Atunci când partea imaginară a unui număr complex este 0, este un număr real pur.
-Dacă partea reală a unui număr complex este 0, atunci numărul este imaginar pur.
-Două numere complexe sunt egale dacă partea lor reală și partea imaginară sunt aceleași.
-Cu numere complexe, se efectuează operațiile cunoscute de adunare, scădere, multiplicare, produs și îmbunătățire, rezultând un alt număr complex.
Reprezentarea numerelor complexe
Numerele complexe pot fi reprezentate în diferite moduri. Iată principalele:
- Forma binomială
Este forma dată la început, unde z este numărul complex, la este partea reală, b este partea imaginară e eu este unitatea imaginară:
z = a + ib
Sau, de asemenea:
z = x + iy
O modalitate de a grafica numărul complex este prin planul complex prezentat în această figură. Axa imaginară Im este verticală, în timp ce axa reală este orizontală și este notată ca Re.
Numărul complex z este reprezentat pe acest plan ca punct de coordonate (X y) sau (a, b), așa cum se face cu punctele planului real.
Distanța de la origine la punctul z este modulul numărului complex, notat ca r, în timp ce φ este unghiul care se formează r cu axa reală.
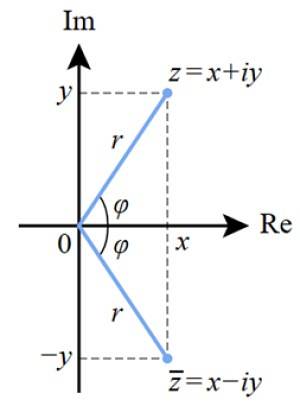
Această reprezentare este strâns legată de cea a vectorilor din planul real. Valoarea lui r corespunde modul a numărului complex.
- Forma polară
Forma polară constă în exprimarea numărului complex dând valorile lui r și de φ. Dacă ne uităm la cifră, valoarea lui r corespunde ipotenuzei unui triunghi dreptunghiular. Picioarele merită la Da b, Ei bine X Da Da.
Din forma binomială sau binomială, ne putem deplasa la forma polară prin:
r = √xDouă+DaDouă
Unghiul φ Este cel care formează segmentul r cu axa orizontală sau axa imaginară. Este cunoscut sub numele de argument a numărului complex. În acest fel:
φ = arctg (y / x)
Argumentul are valori infinite, ținând cont că de fiecare dată când se întoarce un viraj, care valorează 2π radiani, r ocupă din nou aceeași poziție. În acest mod general, argumentul lui z, notat Arg (z), este exprimat astfel:
Arg (z) = φ + 2kπ
Unde k este un număr întreg și este utilizat pentru a indica numărul de rotații întoarse: 2, 3, 4…. Semnul indică direcția de rotație, dacă este în sensul acelor de ceasornic sau invers.
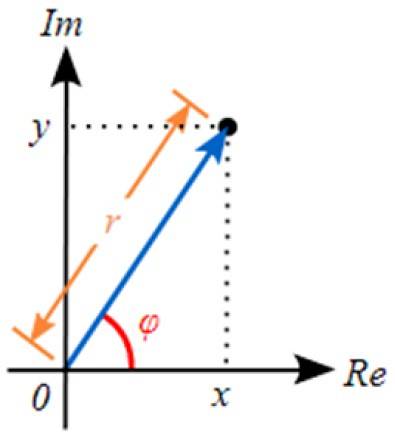
Și dacă vrem să trecem de la forma polară la forma binomială, folosim raporturile trigonometrice. Din figura anterioară putem vedea că:
x = r cos φ
y = r sin φ
În acest fel z = r (cos φ + i sin φ)
Care este abreviat astfel:
z = r cis φ
Exemple de numere complexe
Următoarele numere complexe sunt date sub formă binomială:
a) 3 + i
b) 4
d) -6i
Și acestea sub forma unei perechi ordonate:
a) (-5, -3)
b) (0, 9)
c) (7.0)
În cele din urmă, acest grup este dat în formă polară sau trigonometrică:
a) √2 cis 45º
b) √3 cis 30º
c) 2 cis 315º
Pentru ce sunt?
Utilitatea numerelor complexe depășește rezolvarea ecuației pătratice prezentată la început, deoarece acestea sunt esențiale în domeniul ingineriei și fizicii, în special în:
-Studiul undelor electromagnetice
-Analiza curentului alternativ și a tensiunii
-Modelarea tuturor tipurilor de semnale
-Teoria relativității, în care timpul este presupus a fi o magnitudine imaginară.
Operații de număr complex
Cu numere complexe putem efectua toate operațiile care se fac cu cele reale. Unele sunt mai ușor de făcut dacă numerele apar sub formă binomială, cum ar fi adunarea și scăderea. În schimb, multiplicarea și împărțirea sunt mai simple dacă sunt efectuate cu forma polară.
Să vedem câteva exemple:
- Exemplul 1
Adăugați z1 = 2 + 5i și zDouă = -3 -8i
Soluţie
Părțile reale sunt adăugate separat de părțile imaginare:
z1 + zDouă = (2 + 5i) + (-3 -8i) = -1 -3i
- Exemplul 2
Înmulțiți z1 = 4 cis 45º și zDouă = 5 cis 120º
Soluţie
Se poate arăta că produsul a două numere complexe în formă polară sau trigonometrică este dat de:
z1 . zDouă = r1.rDouă cis (φ1 + φDouă)
În conformitate cu aceasta:
z1 . zDouă = (4 × 5) cis (45 + 120) = 20 cis 165º
Aplicație
O aplicație simplă a numerelor complexe este de a găsi toate rădăcinile unei ecuații polinomiale precum cea prezentată la începutul articolului.
În cazul ecuației xDouă - 10x + 34 = 0, atunci când aplicăm formula de rezolvare obținem:

Prin urmare, soluțiile sunt:
X1 = 5 + 3i
XDouă = 5 - 3i
Referințe
- Earl, R. Numere complexe. Recuperat de la: maths.ox.ac.uk.
- Figuera, J. 2000. Matematica 1. Diversificat. Ediții CO-BO.
- Hoffmann, J. 2005. Selecția subiectelor de matematică. Publicații Monfort.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Wikipedia. Numere complexe. Recuperat de pe: en.wikipedia.org



Nimeni nu a comentat acest articol încă.