
Numere cuantice pentru ce sunt și pentru ce sunt

nnumere cuantice sunt folosite pentru a descrie starea cuantică a electronilor din atom și provin din soluția ecuației Schrödinger pentru cea mai simplă dintre toate: hidrogen.
Ecuația Schrödinger este o ecuație diferențială, ale cărei soluții sunt funcții de undă și sunt notate cu litera greacă ψ. Se pot propune soluții infinite, iar pătratul lor este egal cu probabilitatea de a găsi electronul într-o mică regiune a spațiului, numită orbital.
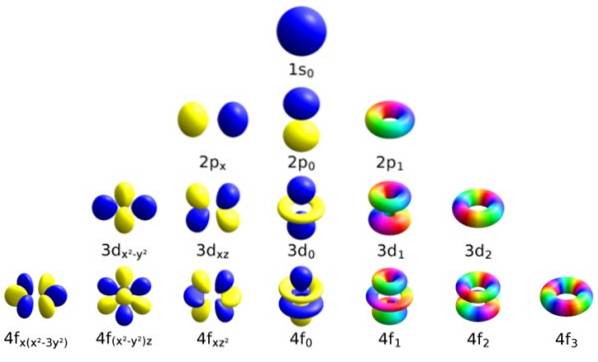
Fiecare orbital are caracteristici definite care îl diferențiază de celelalte, cum ar fi energia, impulsul unghiular și rotirea, o proprietate cuantică a electronului și care este responsabilă, printre altele, de efectele magnetice..
Modul de a identifica fiecare orbital este de a-l distinge printr-un set de numere care îl descriu și acestea sunt tocmai numerele cuantice:
-n: este numărul cuantic principal.
-ℓ: numărul cuantic azimutal.
-mℓ, este numărul magnetic.
-ms, numărul de centrifugare.
Indice articol
- 1 Pentru ce sunt numerele cuantice?
- 1.1 Funcții de undă
- 2 Ce sunt numerele cuantice?
- 2.1 Numărul cuantic principal
- 2.2 Număr cuantic azimutal sau moment unghiular
- 2.3 Număr cuantic magnetic mℓ
- 2.4 Număr cuantic de centrifugare ms
- 3 Referințe
Pentru ce sunt numerele cuantice?
Numerele cuantice sunt folosite pentru a descrie starea electronilor din interiorul atomului. Modelul atomic în care electronul se învârte în jurul nucleului este inexact, deoarece nu este în concordanță cu stabilitatea atomică sau cu un număr mare de fenomene fizice observate..
De aceea danezul Niels Bohr (1885-1962) a făcut o propunere îndrăzneață în 1913: electronul poate fi găsit doar în anumite orbite stabile, a căror dimensiune depinde de un număr întreg numit n.
Mai târziu, în 1925, și fizicianul austriac Erwin Schrödinger (1887-1961) a propus o ecuație diferențială în derivați parțiali, ale căror soluții descriu atomul de hidrogen. Acestea sunt funcțiile de undă ψ menționate la început.
Această ecuație diferențială include cele trei coordonate spațiale plus timpul, dar atunci când aceasta nu este inclusă, soluția ecuației Schrödinger este analogă cu cea a unei unde staționare (o undă care se propagă între anumite limite).
Funcții val
Ecuația Schrödinger independentă de timp este rezolvată în coordonate sferice și soluția este scrisă ca produsul a trei funcții, una pentru fiecare variabilă spațială. În acest sistem de coordonate, în loc să utilizați coordonatele axelor carteziene X, Da Da z se folosesc coordonatele r, θ Da φ. În acest fel:
ψ (r, θ, φ) = R (r) ⋅f (θ) ⋅g (φ)
Funcția de undă este intangibilă, totuși mecanica cuantică ne spune că amplitudinea pătrată:
| ψ (r, θ, φ) |Două
Adică modulul sau valoarea absolută a funcției de undă, pătrat, este un număr real care reprezintă probabilitatea de a găsi electronul, într-o anumită regiune din jurul punctului ale cărui coordonate sunt r, θ Da φ.
Și acest fapt este ceva mai concret și mai tangibil.
Pentru a găsi funcția de undă, trebuie să rezolvați trei ecuații diferențiale obișnuite, una pentru fiecare variabilă r, θ Da φ.
Soluțiile fiecărei ecuații, care vor fi funcțiile R (r), f (θ) și g (φ), conțin primele trei numere cuantice menționate.
Ce sunt numerele cuantice?
Mai jos descriem pe scurt natura fiecărui număr cuantic. Primele trei, așa cum am menționat anterior, apar din soluțiile ecuației Schrödinger.
Al patrulea număr a fost adăugat de Paul Dirac (1902 - 1984) în 1928.
Numărul cuantic principal
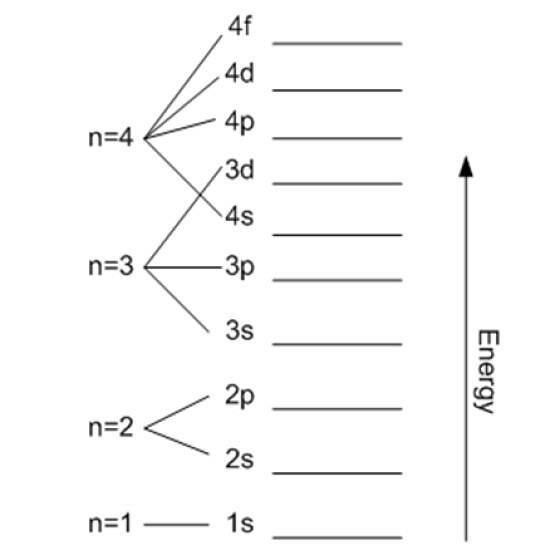
Se notează cu n și indică dimensiunea orbitalului permis, precum și energia electronului. Cu cât valoarea lui este mai mare, cu atât electronul este mai departe de nucleu și energia acestuia va fi și mai mare, dar în schimb își reduce stabilitatea.
Acest număr apare din funcția R (r), care este probabilitatea de a găsi electronul la o anumită distanță r a nucleului, care este determinat de:
-Constanta lui Planck: h = 6,626 × 10 -3. 4 J.s
-Masa electronilor mși = 9,1 × 10-31 kg
-Încărcare electronică: e = 1,6 × 10-19 C.
-Constanta electrostatică: k = 9 × 10 9 N.mDouă/ CDouă
Când n = 1 corespunde razei Bohr care este de aproximativ 5,3 × 10−11 m.
Cu excepția primului strat, celelalte sunt împărțite în sub-straturi sau subnivele. Fiecare înveliș are o energie în electroni volt dată de:

- K (n = 1)
- L (n = 2)
- M (n = 3)
- N (n = 4)
- O (n = 5)
- P (n = 6)
- Q (n = 7).
În teorie nu există o limită superioară pentru n, dar în practică se observă că atinge doar n = 8. Cea mai mică energie posibilă corespunde n = 1 și este cea a stare fundamentală.
Număr cuantic azimutal sau moment unghiular
Notat cu litera cursivă ℓ, acest număr determină forma orbitalilor, cuantificând magnitudinea momentului unghiular orbital al electronului.
Poate lua valori pozitive și între între 0 și n-1, de exemplu:
-Când n = 1, atunci ℓ = 0 și există un singur subnivel.
-Dacă n = 2, atunci ℓ poate fi egal cu 0 sau 1, deci avem două subnivele.
-Și dacă n = 3, atunci ℓ își asumă valorile 0, 1 și 2 și există 3 subnivele.
Poate fi continuat în acest mod la nesfârșit, deși așa cum am spus mai devreme, în practică n se ridică la 8. Subnivelele sunt notate cu literele: s, p, d, F Da g și cresc în energie.

Număr cuantic magnetic mℓ
Acest număr decide orientarea orbitalului în spațiu și valoarea acestuia depinde de cea a lui ℓ.
Pentru un given dat, există (2ℓ + 1) valori întregi ale lui m ℓ, care corespund orbitalilor respectivi. Acestea sunt:
-ℓ, (- ℓ + 1),… 0,… (+ ℓ -1), + ℓ.
Exemplu
Dacă n = 2, știm că ℓ = 0 și ℓ = 1, atunci m ℓ ia următoarele valori:
-Pentru ℓ = 0: m ℓ = 0.
-Pentru ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
Orbitalul n = 2 are două subnivele, primul cu n = 2, ℓ = 0 și m ℓ = 0. Apoi avem al doilea subnivel: n = 2, ℓ = 1, cu 3 orbitali:
- n = 2, ℓ = 1, m ℓ = -1
- n = 2, ℓ = 1, m ℓ = 0
- n = 2, ℓ = 1, m ℓ = +1
Cei trei orbitali au aceeași energie, dar orientare spațială diferită.
Număr cuantic de centrifugare ms
La rezolvarea ecuației Schrödinger în trei dimensiuni, apar numerele deja descrise. Cu toate acestea, în hidrogen se observă o structură și mai fină că aceste numere nu sunt suficiente pentru a explica.
Din acest motiv, în 1921 un alt fizician, Wolfgang Pauli, a propus existența unui al patrulea număr: numărul de spin ms, care ia valori de + ½ sau -½.
Acest număr descrie o proprietate foarte importantă a electronului, care este a învârti, cuvânt care provine din engleză a învârti (a se întoarce pe sine). Și rotația la rândul ei este legată de proprietățile magnetice ale atomului.
O modalitate de a înțelege spinul este să ne imaginăm că electronul se comportă ca un mic dipol magnetic (un magnet cu poli nord și sud), datorită unei rotații în jurul propriei axe. Rotația poate fi în aceeași direcție ca în sensul acelor de ceasornic sau în direcția opusă.
Deși Pauli a sugerat existența acestui număr, rezultatele unui experiment realizat de Otto Stern și Walter Gerlach în 1922 îl anticipaseră deja..
Acești oameni de știință au reușit să împartă un fascicul de atomi de argint în doi prin aplicarea unui câmp magnetic neuniform.
Valoarea ms nu depinde de n, ℓ și m ℓ. În formă grafică, este reprezentată de o săgeată: o săgeată sus indică o virare în sensul acelor de ceasornic și o săgeată în jos indică o virare în sens invers acelor de ceasornic.
Principiul de excludere Pauli
Comportamentul electronilor în atom este rezumat în principiul excluderii Pauli, care afirmă că doi electroni dintr-un atom nu pot exista în aceeași stare cuantică.
Prin urmare, fiecare electron trebuie să aibă un set diferit de numere cuantice n, ℓ, m ℓ si ms.
Importanța numerelor cuantice și acest principiu constă în înțelegerea proprietăților elementelor din tabelul periodic: electronii sunt organizați în straturi în funcție de n, apoi în substraturi în funcție de ℓ și restul numerelor.
Referințe
- Alonso, M. 1971. Fundamente cuantice și statistice. Fondul Interamerican pentru Educație.
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Chang, R. 2013. Chimie. 11. Ediție. Mc Graw Hill Educație.
- Eisberg-Resnick. 1989. Fizica cuantică. Limusa - Wiley.
- Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
- Rex, A. 2011. Fundamentele fizicii. Pearson.
- Tippens, P. 2011. Fizică: concepte și aplicații. Ediția a VII-a. Dealul Mcgraw.



Nimeni nu a comentat acest articol încă.