
Conceptul undelor liniare, caracteristici, exemple
unde liniare sunt acelea în care principiul suprapunerii este aplicabil, adică acelea în care forma de undă și evoluția spațiu-timp pot fi realizate ca suma soluțiilor de bază, de exemplu de tip armonic. Nu toate undele respectă principiul suprapunerii, cele care nu se conformează se numesc unde neliniare.
Denumirea de „liniar” provine din faptul că undele liniare îndeplinesc întotdeauna o ecuație diferențială în derivate parțiale, în care toți termenii care implică variabila dependentă sau derivatele acesteia sunt ridicați la prima putere.

Pe de altă parte, undele neliniare satisfac ecuațiile de undă care au termeni pătratici sau grade mai mari în variabila dependentă sau în derivatele sale.
Undele liniare sunt uneori confundate cu undele longitudinale, care sunt cele în care vibrația are loc în aceeași direcție de propagare, ca undele sonore.
Dar undele longitudinale, precum și undele transversale, pot fi la rândul lor liniare sau neliniare în funcție, printre alți factori, de amplitudinea perturbației inițiale și de mediul în care se propagă..
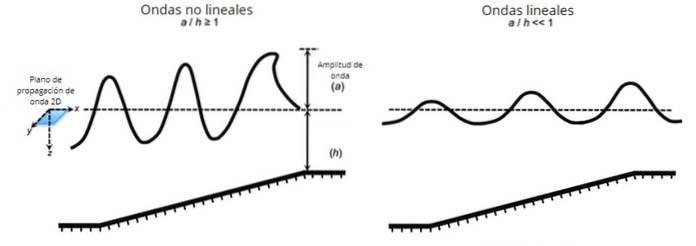
În general, se întâmplă că atunci când perturbarea inițială este de mică amplitudine, ecuația care descrie propagarea undei este liniară sau poate fi liniarizată prin anumite aproximări, deși acest lucru nu este întotdeauna cazul..
Indice articol
- 1 Ecuația diferențială în unde liniare
- 1.1 Soluții ale ecuației diferențiale
- 2 Undele liniare dispersive și non-dispersive
- 2.1 Undele nedispersive
- 2.2 Undele dispersive
- 3 Exemple de unde liniare
- 3.1 Undele electromagnetice
- 3.2 Ecuația Schrödinger
- 3.3 Valuri în ape adânci
- 3.4 Sunetul
- 3.5 Valuri într-o frânghie încordată
- 4 Referințe
Ecuația diferențială în unde liniare
Într-un mediu liniar, o formă de undă limitată în spațiu și timp poate fi reprezentată de suma funcțiilor de undă ale tipului sinus sau cosinus al diferitelor frecvențe și lungimi de undă utilizând seria Fourier.
Undele liniare au asociat întotdeauna o ecuație diferențială de tip liniar, a cărei soluție reprezintă predicția a ceea ce va fi perturbarea în instanțele ulterioare ale unei perturbări inițiale situate spațial la instant.
Ecuația undelor liniare clasice, într-o singură dimensiune spațială, ale cărei soluții sunt unde liniare este:
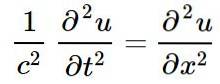
În ecuația de mai sus sau reprezintă perturbarea unei anumite mărimi fizice la poziție X și în clipa aceea t, și anume sau este o funcție a X Da t:
u = u (x, t)
De exemplu, dacă este o undă sonoră în aer, sau poate reprezenta variația presiunii în raport cu valoarea acesteia fără a deranja.
În cazul unei unde electromagnetice, u reprezintă câmpul electric sau câmpul magnetic oscilând perpendicular pe direcția de propagare.
În cazul unei frânghii întinse, sau reprezintă deplasarea transversală în raport cu poziția de echilibru a frânghiei, așa cum se arată în figura următoare:

Soluții ale ecuației diferențiale
Dacă există două sau mai multe soluții ale ecuației diferențiale liniare, atunci fiecare soluție înmulțită cu o constantă va fi o soluție și la fel va fi și suma acestora.
Spre deosebire de ecuațiile neliniare, ecuațiile liniare de undă admit soluții armonice de tipul:
sau1= A⋅sen (k⋅x - ω⋅t) Da sauDouă= A⋅sen (k⋅x + ω⋅t)
Acest lucru poate fi verificat prin simpla substituție în ecuația undelor liniare.
Prima soluție reprezintă o undă călătoare care se deplasează spre dreapta, în timp ce a doua soluție spre stânga rapid c = ω / k.
Soluțiile armonice sunt caracteristice ecuațiilor de undă liniară.
Pe de altă parte, combinația liniară a două soluții armonice este, de asemenea, o soluție a ecuației undei liniare, de exemplu:
u = A1 cos (k1⋅x - ω1⋅t) + ADouă sen (kDouă⋅x - ωDouă⋅t) este soluție.
Cea mai relevantă caracteristică a undelor liniare este că orice formă de undă, oricât de complexă, poate fi obținută printr-o însumare a undelor armonice simple în sinus și cosinus:
u (x, t) = A0 + ∑n LAn cos (kn⋅x - ωn⋅t) + ∑m Bm sen (km⋅x - ωm⋅t).
Undele liniare dispersive și non-dispersive
În ecuația de undă liniară clasică, c reprezintă viteza de propagare a pulsului.
Undele nedispersive
În cazurile în care c este o valoare constantă, de exemplu unde electromagnetice în vid, apoi un impuls în momentul inițial t = 0 Formă f (x) se răspândește în funcție de:
u (x, t) = f (x - c⋅t)
Fără a suferi nicio distorsiune. Când se întâmplă acest lucru, se spune că mediul nu este dispersiv..
Valuri dispersoare
Cu toate acestea, în mediul dispersiv viteza de propagare c poate depinde de lungimea de undă λ, adică: c = c (λ).
Undele electromagnetice sunt dispersive atunci când călătoresc printr-un mediu material. De asemenea, valurile de suprafață ale apei se deplasează cu viteze diferite, în funcție de adâncimea apei.
Viteza cu care o undă armonică de acest tip A⋅sen (k⋅x - ω⋅t) este ω / k = c y se numește viteza de fază. Dacă mediul este dispersiv, atunci c este o funcție a numărului de undă k: c = c (k), Unde k este legată de lungimea de undă de k = 2π / λ.
Rapoarte de dispersie
Relația dintre frecvență și lungimea de undă se numește raport de dispersie, decât exprimat în termeni de frecvență unghiulară ω și numărul de undă k este: ω = c (k) ⋅k.
Unele relații de dispersie caracteristice ale undelor liniare sunt următoarele:
În valurile oceanului unde lungimea de undă (distanța dintre creste) este mult mai mare decât adâncimea H, dar deoarece amplitudinea sa este mult mai mică decât adâncimea, relația de dispersie este:
ω = √ (gH) ⋅k
De acolo se concluzionează că se propagă cu viteză constantă √ (gH) (mediu nedispersiv).
Dar valurile din apele foarte adânci sunt dispersive, deoarece raportul lor de dispersie este:
ω = √ (g / k) ⋅k
Aceasta înseamnă că viteza de fază ω / k este variabilă și depinde de numărul de undă și, prin urmare, de lungimea de undă a undei.
Viteza grupului
Dacă două unde liniare armonice se suprapun, dar avansează la viteze diferite, atunci viteza grupului (adică a pachetului de unde) nu se potrivește cu viteza de fază.
Viteza grupului vg este definit ca derivata frecvenței în raport cu numărul de undă în relația de dispersie: vg = ω '(k).
Următoarea figură arată suprapunerea sau suma a două unde armonice sau1= A⋅sen (k1⋅x - ω1⋅t) Da sauDouă= A⋅sen (kDouă⋅x - ωDouă⋅t) călătorind cu viteze diferite v1= ω1/ k1 Da vDouă= ωDouă/ kDouă. Observați cum viteza grupului este diferită de viteza fazei, în acest caz viteza grupului este ∆ω / ∆k.
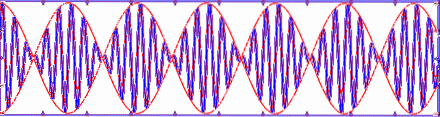
În funcție de raportul de dispersie, se poate întâmpla chiar ca viteza de fază și viteza de grup, în unde liniare, să aibă direcții opuse..
Exemple de unde liniare
Undele electromagnetice

Undele electromagnetice sunt unde liniare. Ecuația sa de undă este derivată din ecuațiile electromagnetismului (ecuațiile lui Maxwell) care sunt, de asemenea, liniare.
Ecuația Schrödinger
Este ecuația care descrie dinamica particulelor pe o scară atomică, unde caracteristicile undei sunt relevante, de exemplu cazul electronilor din atom.
Deci, „unda electronică” sau funcția de undă așa cum se mai numește, este o undă liniară.
Valuri în apă adâncă
Undele liniare sunt, de asemenea, acelea în care amplitudinea este mult mai mică decât lungimea de undă și lungimea de undă mult mai mare decât adâncimea. Valurile din apele adânci urmează teoria liniară (cunoscută sub numele de teoria valului aerisit).
Cu toate acestea, valul care se apropie de țărm și formează creasta caracteristică de curling (și pe care surferii îl iubesc) este o undă neliniară..
Sunet
Deoarece sunetul este o mică perturbare a presiunii atmosferice, este considerat o undă liniară. Cu toate acestea, unda de șoc dintr-o explozie sau frontul de undă de la o aeronavă supersonică sunt exemple tipice de undă neliniară..
Valuri pe o frânghie încordată
Undele care se propagă printr-o frânghie tensionată sunt liniare, atât timp cât pulsația inițială este de mică amplitudine, adică limita elastică a frânghiei nu este depășită..
Undele liniare din corzi sunt reflectate la capetele lor și se suprapun, dând naștere la valuri staționare sau moduri vibraționale care dau tonurile armonice și subarmonice caracteristice instrumentelor cu coarde..
Referințe
- Griffiths G și Schiesser W. Valuri liniare și neliniare. Recuperat de pe: sholarpedia.org.
- Whitham G.B. (1999) „Valuri liniare și neliniare”. Wiley.
- Wikipedia. Undele neliniare. Recuperat de pe: es.wikipedia.com
- Wikipedia. Acustic neliniar. Recuperat de pe: en.wikipedia.com
- Wikipedia. Valuri. Recuperat de pe: en.wikipedia.com
- Wikiwaves. Undele neliniare. Recuperat de pe: wikiwaves.org

Nimeni nu a comentat acest articol încă.