
Formula potențială electrică și ecuații, calcul, exemple, exerciții
potential electric este definit în orice punct în care există un câmp electric, ca energia potențială a acelui câmp pe unitate de încărcare. Sarcinile punctuale și distribuțiile punctuale sau continue ale sarcinii produc un câmp electric și, prin urmare, au un potențial asociat.
În Sistemul Internațional de Unități (SI), potențialul electric este măsurat în volți (V) și este notat ca V. Matematic se exprimă ca:
V = U / qsau

Unde U este energia potențială asociată cu sarcina sau distribuția și qsau este o sarcină de test pozitivă. Deoarece U este un scalar, la fel este și potențialul.
Din definiție, 1 volt este pur și simplu 1 Joule / Coulomb (J / C), unde Joule este unitatea SI pentru energie și Coulomb (C) este unitatea pentru încărcarea electrică..
Să presupunem o încărcare punctuală q. Putem verifica natura câmpului pe care îl produce această sarcină utilizând o sarcină de testare mică, pozitivă, numită qsau, folosit ca sondă.
Lucrarea W necesară pentru a muta această sarcină mică din punct la până la punct b, este negativul diferenței de energie potențială ΔU între aceste puncte:
Wa → b = -ΔU = - (Ub - SAUla)
Împărțind totul între qsau:
Wa → b / qsau= - ΔU / qsau = - (Ub - SAUla) / qsau = - (Vb - Vla) = -ΔV
Aici Vb este potențialul la punctul b și Vla este cel al punctului a. Diferența de potențial Vla - Vb este potențialul despre b și se numește Vab. Ordinea indicilor este importantă, dacă s-ar schimba atunci ar reprezenta potențialul b cu privire la a.
Indice articol
- 1 Diferența de potențial electric
- 1.1 Semne și valori pentru diferența de potențial
- 2 Cum se calculează potențialul electric?
- 2.1 Potențial electric pentru distribuții discrete de încărcare
- 2.2 Potențial electric în distribuții continue de sarcină
- 3 Exemple de potențial electric
- 3.1 Baterii și baterii
- 3.2 Priză
- 3.3 Tensiunea dintre norii încărcați și sol
- 3.4 Generator Van Der Graff
- 3.5 Electrocardiograma și electroencefalograma
- 4 Exercițiul a fost rezolvat
- 4.1 Soluția a
- 4.2 Soluția b
- 4.3 Soluția c
- 4.4 Soluția d
- 4.5 Soluția e
- 4.6 Soluție f
- 5 Referințe
Diferența de potențial electric
Din cele de mai sus rezultă că:
-ΔV = Wa → b / qsau
Prin urmare:
ΔV = -Wa → b / qsau
Acum, munca este calculată ca integrală a produsului scalar între forța electrică F între q și qsau iar vectorul de deplasare dℓ între punctele a și b. Deoarece câmpul electric este forța pe unitate de încărcare:
ȘI = F/ qsau
Lucrarea pentru a transporta sarcina de testare de la a la b este:
Această ecuație oferă modalitatea de a calcula direct diferența de potențial dacă câmpul electric al sarcinii sau distribuția care o produce este cunoscut anterior..
Și, de asemenea, se observă că diferența de potențial este o cantitate scalară, spre deosebire de câmpul electric, care este un vector.
Semne și valori pentru diferența de potențial
Din definiția anterioară observăm că dacă ȘI și dℓ sunt perpendiculare, diferența de potențial ΔV este zero. Acest lucru nu înseamnă că potențialul în astfel de puncte este zero, ci pur și simplu Vla = Vb, adică potențialul este constant.
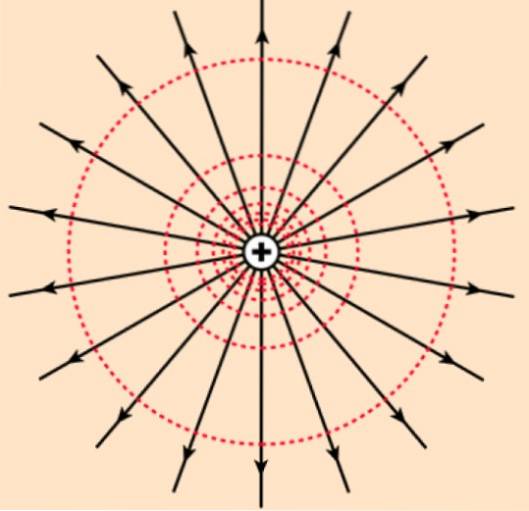
Liniile și suprafețele unde se întâmplă acest lucru sunt numite echipotențial. De exemplu, liniile echipotențiale ale câmpului unei sarcini punctuale sunt circumferințe concentrice sarcinii. Iar suprafețele echipotențiale sunt sfere concentrice.
Dacă potențialul este produs de o sarcină pozitivă, al cărei câmp electric constă în linii radiale care proiectează sarcina, pe măsură ce ne îndepărtăm de câmp, potențialul va deveni din ce în ce mai puțin. Ca sarcină de test qsau este pozitiv, simțiți mai puțină repulsie electrostatică cu cât sunteți mai departe de q.

Dimpotrivă, dacă sarcina ce este negativ, sarcina testului qsau (pozitiv) va avea un potențial mai mic pe măsură ce se apropie ce.
Cum se calculează potențialul electric?
Integrala dată mai sus servește pentru a găsi diferența de potențial și, prin urmare, potențialul la un moment dat b, dacă potențialul de referință este cunoscut într-un alt punct la.
De exemplu, este cazul unei sarcini punctuale ce, al cărui vector de câmp electric într-un punct situat la distanță r a sarcinii este:
ȘI = kq / rDouă r
Unde k este constanta electrostatică a cărei valoare în unități ale sistemului internațional este:
k = 9 x 10 9 NmDouă / CDouă.
Și vectorul r este vectorul unitar de-a lungul liniei de unire ce cu punctul P.
Este înlocuit în definiția ΔV:

Alegerea acestui punct b fi la distanță r a sarcinii și că atunci când a → ∞ potențialul este 0, atunci Vla = 0 și ecuația anterioară este următoarea:
V = kq / r
Alegeți Vla = 0 atunci când un → ∞ are sens, deoarece într-un punct foarte îndepărtat de sarcină, este dificil să percepem că există.
Potențial electric pentru distribuții discrete de încărcare
Când există multe sarcini punctuale distribuite într-o regiune, se calculează potențialul electric pe care îl produc în orice punct P din spațiu, adăugând potențialele individuale pe care le produce fiecare. A) Da:
V = V1 + VDouă + V3 +… VN = ∑ Veu
Suma se extinde de la i = la N și potențialul fiecărei sarcini este calculat folosind ecuația dată în secțiunea anterioară.
Potențial electric în distribuții continue de sarcină
Pornind de la potențialul unei încărcări punctuale, putem găsi potențialul produs de un obiect încărcat, cu o dimensiune măsurabilă, în orice punct P.
Pentru a face acest lucru, corpul este împărțit în multe sarcini infinitezimale mici dq. Fiecare contribuie la întregul potențial cu un dV infinitezimal.

Apoi toate aceste contribuții sunt adăugate printr-o integrală și astfel se obține potențialul total:

Exemple de potențial electric
Există potențial electric în diferite dispozitive datorită cărora este posibil să se obțină energie electrică, de exemplu baterii, baterii auto și prize electrice. Potențialele electrice sunt, de asemenea, stabilite în natură în timpul furtunilor electrice.
Baterii și Baterii
În celule și baterii, energia electrică este stocată prin reacții chimice în interiorul lor. Acestea apar atunci când circuitul este închis, permițând curgerea continuă să curgă și să se aprindă un bec sau motorul de pornire al mașinii să funcționeze..
Există diferite tensiuni: 1,5 V, 3 V, 9 V și 12 V sunt cele mai frecvente.
Outlet
Aparatele și aparatele care funcționează cu electricitate comercială AC sunt conectate la o priză încastrată. În funcție de locație, tensiunea poate fi de 120 V sau 240 V.

Tensiunea dintre norii încărcați și sol
Este cea care apare în timpul furtunilor electrice, datorită mișcării sarcinii electrice prin atmosferă. Poate fi de ordinul a 108 V.

Generator Van Der Graff
Datorită unei benzi transportoare din cauciuc, se produce o sarcină de frecare, care se acumulează pe o sferă conductivă plasată deasupra unui cilindru izolant. Acest lucru generează o diferență de potențial care poate fi de câteva milioane de volți.

Electrocardiogramă și electroencefalogramă
În inimă există celule specializate care polarizează și depolarizează, provocând diferențe de potențial. Acestea pot fi măsurate în funcție de timp prin intermediul unei electrocardiograme..
Acest test simplu se realizează prin plasarea electrozilor pe pieptul persoanei, capabili să măsoare semnale mici..
Deoarece sunt tensiuni foarte mici, trebuie să le amplificați convenabil, apoi să le înregistrați pe o bandă de hârtie sau să le urmăriți prin computer. Medicul analizează pulsurile pentru anomalii și astfel detectează problemele cardiace.

Activitatea electrică a creierului poate fi, de asemenea, înregistrată printr-o procedură similară, numită EEG..
Exercițiul a fost rezolvat
O incarcare Î = - 50,0 nC este situat la 0,30 m de punct LA și 0,50 m de punctul B, așa cum se arată în figura următoare. Răspunde la următoarele întrebări:
a) Care este potențialul în A produs de această încărcare?
b) Și care este potențialul din B?
c) Dacă o sarcină q se deplasează de la A la B, care este diferența de potențial prin care se mișcă?
d) Potrivit răspunsului anterior, potențialul său crește sau scade??
e) Dacă q = - 1,0 nC, care este schimbarea energiei sale potențiale electrostatice pe măsură ce se deplasează de la A la B?
f) Câtă muncă face câmpul electric produs de Q pe măsură ce sarcina de testare se deplasează de la A la B?

Solutie la
Q este o sarcină punctuală, prin urmare potențialul său electric în A este calculat prin:
VLA = kQ / rLA = 9 x 109 x (-50 x 10-9) / 0,3 V = -1500 V
Soluția b
In acelasi fel
VB = kQ / rB = 9 x 109 x (-50 x 10-9) / 0,5 V = -900 V
Soluția c
ΔV = Vb - Vla = -900 - (-1500) V = + 600 V
Soluția d
Dacă încărcarea q este pozitivă, potențialul său crește, dar dacă este negativ, potențialul său scade.
Soluția e
ΔV = ΔU / qsau → ΔU = qsau ΔV = -1,0 x 10-9 x 600 J = -6,0 x 10-7 J.
Semnarea negativă ΔU indică faptul că energia potențială din B este mai mică decât cea a lui A.
Soluția f
De când W = -ΔU câmpul își dă seama +6,0 x 10-7 J de muncă.
Referințe
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 5. Electrostatice. Editat de Douglas Figueroa (USB).
- Giambattista, A. 2010. Fizică. Al 2-lea. Ed. McGraw Hill.
- Resnick, R. (1999). Fizic. Vol. 2. Ediția a 3-a. În spaniolă. Compañía Editorial Continental S.A. de C.V.
- Tipler, P. (2006) Fizică pentru știință și tehnologie. Ediția a 5-a Volumul 2. Editorial Reverté.
- Serway, R. Fizică pentru știință și inginerie. Volumul 2. 7. Ed. Cengage Learning.



Nimeni nu a comentat acest articol încă.