
Prima explicație a condiției de echilibru, exemple, exerciții
prima condiție de echilibru necesită ca suma vectorială a tuturor forțelor care acționează asupra unui corp să fie zero, astfel încât să fie în repaus (echilibru static) sau cu mișcare rectilinie uniformă (echilibru dinamic).
Această sumă de forțe nu este alta decât forța netă care acționează asupra corpului, exprimată matematic în acest fel:
Fnet = 0
∑ F = 0

În spațiu, prima condiție de echilibru dă naștere la trei ecuații, una pentru fiecare dimensiune:
∑ FX = 0; ∑ FDa = 0 și ∑ Fz = 0
Când aceste ecuații sunt satisfăcute, obiectul nu se traduce sau, dacă se întâmplă, va fi cu viteză constantă.
Privind în jurul nostru ne dăm seama că căutăm continuu să satisfacem prima condiție de echilibru, astfel încât lucrurile să nu cadă.
Prin urmare, caută să compenseze atracția gravitațională a Pământului prin intermediul unor suporturi, frânghii sau suporturi ale unora, astfel încât lucrurile să rămână la locul lor și să nu ajungă la sol..
Alteori este necesar să se împiedice câmpurile electromagnetice externe să interfereze cu funcționarea circuitelor electrice și a dispozitivelor de comunicații. În acest caz, sarcinile electrice trebuie să fie în echilibru..
Indice articol
- 1 Exemple
- 1.1 Clădiri
- 1.2 Semafoare și semne suspendate
- 1.3 Conductori în echilibru electrostatic
- 1.4 Lămpi de tavan
- 1.5 Cărți și obiecte pe mese
- 1.6 Măsurarea vâscozității unui lichid
- 2 pași pentru aplicarea primei condiții de echilibru
- 3 exerciții rezolvate
- 3.1 - Exercițiu rezolvat 1
- 3.2 - Exercițiu rezolvat 2
- 4 Subiecte de interes
- 5 Referințe
Exemple
Un număr mare de obiecte de zi cu zi îndeplinesc prima condiție de echilibru, este o chestiune de a observa cu atenție:
Clădiri
Constructorii caută stabilitate în construcții, astfel încât utilizatorii să rămână în siguranță. Obiectivul staticii este de a studia condițiile pentru ca echilibrul static să se producă în clădiri, poduri, drumuri și tot felul de structuri..
Semafoare și semne suspendate
Aceste dispozitive de semnalizare trebuie să rămână fixe pentru a-și îndeplini funcțiile, prin urmare sunt ținute de cabluri, stâlpi și tije în așa fel încât să fie îndeplinită prima condiție de echilibru..

Conductori în echilibru electrostaticpenthouse
Când materialele conductoare precum cuprul și alte metale dobândesc o sarcină electrică, echilibrul electrostatic este stabilit în curând, lăsând excesul de sarcină pe suprafața conductoare. În interiorul câmpului electric este zero.
Acest efect este adesea folosit pentru a izola echipamentele electrice și electronice de câmpurile externe, folosind așa-numita cușcă Faraday. Cușca este realizată din material conductiv și înconjoară echipamentul care trebuie protejat.
În timpul furtunilor, automobilele servesc drept cuști Faraday, protejând ocupanții de șocurile electrice..
Lămpi de tavan
În sistemele de iluminat, cum ar fi lămpile suspendate, prima condiție de echilibru este utilizată pentru a le fixa pe tavan, podea sau perete.

Cărți și obiecte pe mese
Obiectele așezate pe mese și rafturi îndeplinesc prima condiție de echilibru. Forța normală pe care suportul o exercită asupra obiectelor este responsabilă pentru compensarea greutății.
Măsurarea vâscozității unui lichid
Pentru a determina vâscozitatea unui lichid, un obiect sferic cu diametrul cunoscut este aruncat în interiorul său și viteza acestuia va încetini din cauza rezistenței. Viteza sferei este constantă, fiind astfel în echilibru dinamic.
Cu cât vâscozitatea lichidului este mai mare, cu atât este mai mică viteza cu care se deplasează sfera în interior.
Pași pentru aplicarea primei condiții de echilibru
-Realizați o diagramă a corpului liber, arătând toate forțele care acționează asupra corpului (omiteți-le pe cele pe care corpul le exercită asupra altora).
-Selectați un sistem de coordonate cartezian, asigurându-vă că, pe cât posibil, forțele sunt situate pe oricare dintre axe. Direcția pozitivă se ia de obicei în direcția mișcării sau a unei posibile mișcări.
-Determinați componentele carteziene ale fiecărei forțe.
-Aplicarea celei de-a doua legi a lui Newton pentru fiecare componentă, astfel cum a fost stabilită la început, rămâne astfel un sistem de ecuații.
-Rezolvați sistemul de ecuații ridicat în pasul anterior.
Exerciții rezolvate
- Exercițiu rezolvat 1
Blocul figurii, al masei m, se deplasează în jos pe planul înclinat la unghiul θ cu viteză constantă. Calculați valoarea coeficientului de frecare cinetică μk, dacă masa blocului este m = 5 kg și θ = 37º.

Soluţie
Primul pas este de a desena diagrama corpului liber și de a alege un sistem de coordonate carteziene pentru a exprima vectorial fiecare forță. Forțele care acționează asupra blocului sunt:
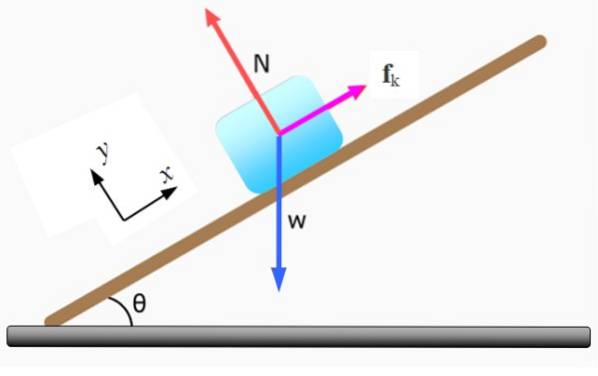
-Normalul N exercitat de planul înclinat, este perpendicular pe suprafața acestuia.
-Greutatea W este îndreptat vertical în jos.
-Fricțiune cinetică Fk care se opune mișcării. Dacă nu ar exista, corpul s-ar deplasa în jos cu o accelerație egală cu g.senθ.
Ca și greutatea W este înclinat în raport cu axele de coordonate selectate, acesta trebuie descompus în componentele sale carteziene:
WX = mg sin 37º = 5 kg x 9,8 m / sDouă x sin 37º = 29. 5 N
WDa = mg.cos 37º = 5 kg x 9,8 m / sDouă x cos 37º = 39,1 N
A doua lege a lui Newton este acum aplicată, setând fiecare sumă la 0, deoarece blocul nu are accelerație atunci când se deplasează cu viteză constantă:
∑ FDa = N - WDa = 0
∑ FX = WX - Fk = 0
Mărimea frecării cinetice este proporțională cu magnitudinea normalului, coeficientul de frecare cinetic fiind μk constanta proporționalității.
Fk = μk N
In acelasi timp:
N = WDa = 39,1 N
La care se adauga:
Fk = WX
Prin urmare:
- 5 N = μk x 39,1 N
μk = 29. 5 / 39.1 = 0.75
- Exercițiu rezolvat 2
Calculați magnitudinea tensiunilor care susțin semaforul cu masa de 33 kg, prezentat în figură:
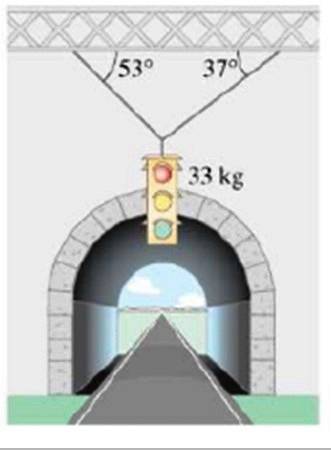
Soluţie
Diagrama corpului liber este realizată atât pentru semafor, cât și pentru nodul care ține cablurile:
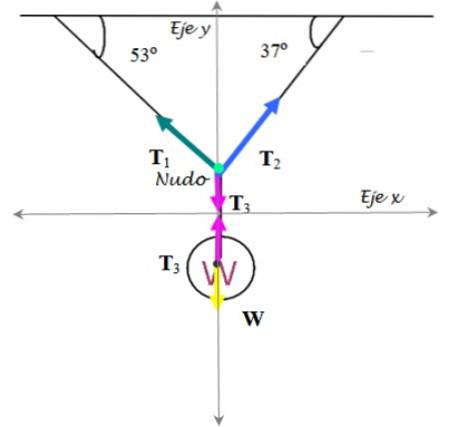
Semafor
Pe el acționează: tensiunea T3 în sus și greutatea W în jos. Prin urmare:
∑ FDa = W - T3 = 0
Prin urmare:
T3 = 33 kg x 9,8 m / sDouă = 323,4 N
Nod
Tensiunile sunt descompuse în componentele lor carteziene:
∑ FDa = T1 sin 53º + TDouă sen 37º - T3 = 0
∑ FX = TDouă cos 37º - T1 cos 53º = 0
Și următorul sistem de ecuații liniare este obținut cu două necunoscute T1 Si tDouă :
- 0,6 T1 + 0,8 TDouă = 0
0,8 T1 + 0,6 TDouă = 323,4
Soluția acestui sistem de ecuații este: T1 = 258,7 N și TDouă = 194,0 N
Teme de interes
Condiții de echilibru.
A doua condiție de echilibru.
Referințe
- Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 4. Sisteme de particule. Editat de Douglas Figueroa (USB).
- Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.
- Wikipedia. Statice (mecanice). Recuperat de pe: es.wikipedia.org.



Nimeni nu a comentat acest articol încă.