
Formula probabilității condiționale și ecuații, proprietăți, exemple
probabilitate condițională Este posibilitatea apariției unui anumit eveniment, având în vedere că altul apare ca o condiție. Aceste informații suplimentare pot (sau nu) să modifice percepția că se va întâmpla ceva.
De exemplu, ne putem întreba: „Care este probabilitatea ca astăzi să plouă, având în vedere că nu a plouat de două zile?” Evenimentul pentru care vrem să știm probabilitatea este că plouă astăzi, iar informațiile suplimentare care ar condiționa răspunsul este că „nu a plouat de două zile”.

Fii un spațiul probabilistic compus din Ω (spațiul eșantionului), ℬ (evenimentele aleatorii) și P (probabilitatea fiecărui eveniment), plus evenimentele A și B care aparțin lui ℬ.
Probabilitatea condițională ca A să apară, având în vedere că a apărut B, care este notată ca P (A│B), este definită după cum urmează:
P (A│B) = P (A∩B) / P (B) = P (A și B) / P (B)
În cazul în care: P (A) este probabilitatea apariției lui A, P (B) este probabilitatea evenimentului B și este diferită de 0, iar P (A∩B) este probabilitatea intersecției dintre A și B, adică ,, probabilitatea ca ambele evenimente să apară (probabilitate comună).
Aceasta este o expresie pentru teorema lui Bayes aplicată la două evenimente, propusă în 1763 de teologul și matematicianul englez Thomas Bayes.
Indice articol
- 1 Proprietăți
- 1.1 Regula generală a înmulțirii
- 2 Exemple de probabilitate condiționată
- 2.1 - Exemplul 1
- 2.2 - Exemplul 2
- 3 Exercițiul a fost rezolvat
- 4 Referințe
Proprietăți
-Fiecare probabilitate condițională este între 0 și 1:
0 ≤ P (A│B) ≤ 1
-Probabilitatea ca evenimentul A să apară, dat fiind faptul că apare evenimentul, este evident 1:
P (A│A) = P (A∩A) / P (A) = P (A) / P (A) = 1
-Dacă două evenimente sunt exclusive, adică evenimente care nu se pot întâmpla simultan, atunci probabilitatea condițională ca unul dintre ele să se întâmple este 0, deoarece intersecția este nulă:
P (A│B) = P (A∩B) / P (B) = 0 / P (B) = 0
-Dacă B este un subset al lui A, atunci probabilitatea condițională este și 1:
P (B│A) = P (A∩B) / P (A) = 1
Important
P (A│B) nu este în general egal cu P (B│A), de aceea trebuie să fim atenți să nu schimbăm evenimentele atunci când găsim probabilitatea condițională.
Regula generală a multiplicării
De multe ori doriți să găsiți probabilitatea comună P (A∩B), mai degrabă decât probabilitatea condițională. Apoi, prin următoarea teoremă avem:
P (A∩B) = P (A și B) = P (A│B). P (B)
Teorema poate fi extinsă pentru trei evenimente A, B și C:
P (A∩B∩C) = P (A și B și C) = P (A) P (B│A) P (C│A∩B)
Și, de asemenea, pentru diverse evenimente, cum ar fi A1, LADouă, LA3 și mai mult, poate fi exprimat după cum urmează:
P (A1∩ ADouă ∩ A3… ∩ An) = P (A1). P (ADouă│A1). P (A3│A1∩ ADouă) ... P (An││A1∩ ADouă∩ ... An-1)
Atunci când este cazul evenimentelor care apar în succesiune și prin diferite etape, este convenabil să organizați datele într-o diagramă sau într-un tabel. Acest lucru facilitează vizualizarea opțiunilor pentru a atinge probabilitatea solicitată..
Exemple în acest sens sunt diagramă de copac si tabelul de contingență. Din una dintre ele o poți construi pe cealaltă.
Exemple de probabilitate condiționată
Să vedem câteva situații în care probabilitățile unui eveniment sunt modificate de apariția altuia:
- Exemplul 1
Două tipuri de prăjituri sunt vândute într-un magazin de dulciuri: căpșuni și ciocolată. Prin înregistrarea preferințelor a 50 de clienți de ambele sexe, s-au determinat următoarele valori:
-27 de femei, dintre care 11 preferă tortul cu căpșuni și 16 tort cu ciocolată.
-23 de bărbați: 15 aleg ciocolată și 8 căpșuni.
Probabilitatea ca un client să aleagă o prăjitură de ciocolată poate fi determinată prin aplicarea regulii lui Laplace, conform căreia probabilitatea oricărui eveniment este:
P = numărul de evenimente favorabile / numărul total de evenimente
În acest caz, din 50 de clienți, un total de 31 preferă ciocolata, deci probabilitatea ar fi P = 31/50 = 0,62. Adică 62% dintre clienți preferă tortul cu ciocolată.
Dar ar fi diferit dacă clientul este o femeie? Acesta este un caz de probabilitate condiționată.
Tabel de contingență
Folosind un tabel de contingență ca acesta, totalurile sunt ușor afișate:
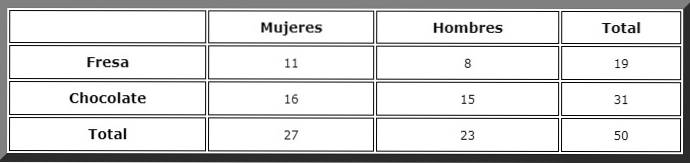
Apoi se observă cazurile favorabile și se aplică regula lui Laplace, dar mai întâi definim evenimentele:
-B este evenimentul „client de sex feminin”.
-A este evenimentul „preferă tortul cu ciocolată” fiind femeie.
Mergem la coloana cu eticheta „femei” și acolo vedem că totalul este de 27.
Atunci se caută cazul favorabil în rândul „ciocolată”. Există 16 dintre aceste evenimente, prin urmare probabilitatea căutată este, în mod direct:
P (A│B) = 16/27 = 0,5924
59,24% dintre clienții de sex feminin preferă tortul cu ciocolată.
Această valoare coincide atunci când o contrastăm cu definiția dată inițial a probabilității condiționale:
P (A│B) = P (A∩B) / P (B)
Ne asigurăm că folosim regula lui Laplace și valorile tabelului:
P (B) = 27/50
P (A și B) = 16/50
Unde P (A și B) este probabilitatea ca clientul să prefere ciocolata și să fie o femeie. Acum valorile sunt substituite:
P (A│B) = P (A și B) / P (B) = (16/50) / (27/50) = 16/27 = 0,5924.
Și este dovedit că rezultatul este același.
- Exemplul 2
În acest exemplu se aplică regula multiplicării. Să presupunem că există pantaloni în trei dimensiuni expuse într-un magazin: mic, mediu și mare..
Într-un lot cu un total de 24 de pantaloni, din care există 8 din fiecare mărime și toți sunt amestecați, care ar fi probabilitatea de a extrage doi dintre ei și că ambii erau mici?
Este clar că probabilitatea de a scoate un mic pantalon la prima încercare este de 8/24 = 1/3. Acum, a doua extracție este condiționată de primul eveniment, deoarece atunci când scoateți o pereche de pantaloni, nu mai există 24, ci 23. Și dacă un pantalon mic este îndepărtat, există 7 în loc de 8.
Evenimentul A trage un pantalon mic, după ce a tras altul la prima încercare. Și evenimentul B este cel cu pantalonii mici pentru prima dată. Prin urmare:
P (B) = 1/3; P (A│B) = 7/24
În cele din urmă, folosind regula multiplicării:
P (A∩B) = (7/24). (1/3) = 7/72 = 0,097
Exercițiul a fost rezolvat
Într-un studiu de punctualitate pe zborurile aeriene comerciale, sunt disponibile următoarele date:
-P (B) = 0,83, este probabilitatea ca un avion să decoleze la timp.
-P (A) = 0,81, este probabilitatea aterizării la timp.
-P (B∩A) = 0,78 este probabilitatea ca zborul să ajungă la timp decolând la timp.
Se cere calcularea:
a) Care este probabilitatea ca avionul să aterizeze la timp având în vedere că a decolat la timp?
b) Probabilitatea anterioară este aceeași cu probabilitatea de a pleca la timp dacă a reușit să aterizeze la timp??
c) Și, în cele din urmă: care este probabilitatea ca acesta să ajungă la timp având în vedere acest lucru nu a ieșit la timp?

Solutie la
Pentru a răspunde la întrebare, se utilizează definiția probabilității condiționate:
P (A│B) = P (A∩B) / P (B) = P (A și B) / P (B) = 0,78 / 0,83 = 0,9398
Soluția b
În acest caz, evenimentele din definiție sunt schimbate:
P (B│A) = P (A∩B) / P (A) = P (A și B) / P (A) = 0,78 / 0,81 = 0,9630
Rețineți că această probabilitate este ușor diferită de cea precedentă, așa cum am subliniat anterior.
Soluția c
Probabilitatea de a nu pleca la timp este 1 - P (B) = 1 - 0,83 = 0,17, îl vom numi P (B)C), deoarece este evenimentul complementar pentru a decola la timp. Probabilitatea condițională căutată este:
P (A│BC) = P (A∩BC) / P (BC) = P (A și BC) / P (BC)
Pe de altă parte:
P (A∩BC) = P (aterizare la timp) - P (aterizare la timp și decolare la timp) = 0,81-0,78 = 0,03
În acest caz, probabilitatea condiționată căutată este:
P (A│BC) = 0,03 / 0,17 = 0,1765
Referințe
- Canavos, G. 1988. Probabilitate și statistici: aplicații și metode. Dealul Mcgraw.
- Devore, J. 2012. Probabilități și statistici pentru inginerie și știință. A 8-a. Ediție. Cengage.
- Lipschutz, S. 1991. Seria Schaum: Probabilitate. Dealul Mcgraw.
- Obregón, I. 1989. Teoria probabilității. Editorial Limusa.
- Walpole, R. 2007. Probabilități și statistici pentru inginerie și științe. Pearson.
- Wikipedia. Probabilitate condițională. Recuperat de pe: es.wikipedia.org.

Nimeni nu a comentat acest articol încă.