
Adunarea, multiplicarea, exemplele, exercițiile de proprietate asociativă
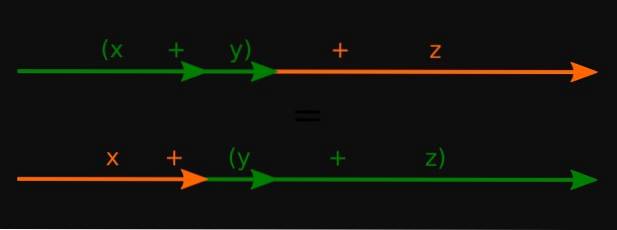
Proprietate asociativă a sumei reprezintă caracterul asociativ al operației de sumă în diferite seturi matematice. În el, trei (sau mai multe) elemente ale acestor seturi sunt legate, numite a, b și c, astfel încât este întotdeauna adevărat:
a + (b + c) = (a + b) + c
În acest fel se garantează că, indiferent de modul de grupare pentru a efectua operația, rezultatul este același.

Dar trebuie remarcat faptul că proprietatea asociativă nu este sinonimă cu proprietatea comutativă. Adică știm că ordinea suplimentelor nu modifică suma sau că ordinea factorilor nu modifică produsul. Deci pentru sumă se poate scrie astfel: a + b = b + a.
Cu toate acestea, în proprietatea asociativă este diferit, deoarece ordinea elementelor care trebuie adăugate este menținută și ce modificări este operația care se execută mai întâi. Ceea ce înseamnă că nu contează să adăugați primul (b + c) și la acest rezultat să adăugați a, decât să începeți să adăugați a cu b și la rezultat să adăugați c.
Multe operații importante, cum ar fi adunarea, sunt asociative, dar nu toate. De exemplu, în scăderea numerelor reale se întâmplă că:
a - (b - c) ≠ (a - b) - c
Dacă a = 2, b = 3, c = 1, atunci:
2- (3 - 1) ≠ (2 - 3) - 1
0 ≠ -2
Indice articol
- 1 Proprietatea asociativă a multiplicării
- 1.1 Aplicații ale proprietății asociative a multiplicării
- 2 Exemple
- 2.1 Proprietatea asociativă în vectori
- 2.2 Factorizarea polinoamelor prin gruparea de termeni
- 3 Exerciții
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 4 Referințe
Proprietatea asociativă a multiplicării
Așa cum s-a făcut pentru adunare, proprietatea asociativă a multiplicării afirmă că:
a ˟ (b ˟ c) = (a ˟ b) ˟ c
În cazul setului de numere reale, este ușor să verificați că acesta este întotdeauna cazul. De exemplu, folosind valorile a = 2, b = 3, c = 1, avem:
Două ˟ (3 ˟ 1) = (2 ˟ 3) ˟ 1 → 2 ˟ 3 = 6 ˟ 1
6 = 6
Numerele reale îndeplinesc proprietatea asociativă atât a adunării, cât și a multiplicării. Pe de altă parte, într-un alt set, cum ar fi cel al vectorilor, suma este asociativă, dar produsul încrucișat sau produsul vector nu este..
Aplicații ale proprietății asociative a multiplicării
Un avantaj al operațiunilor în care este îndeplinită proprietatea asociativă este acela de a putea grupa în cel mai convenabil mod. Acest lucru face rezoluția mult mai ușoară..
De exemplu, să presupunem că într-o bibliotecă mică există 3 rafturi cu câte 5 rafturi. În fiecare raft sunt 8 cărți. Câte cărți sunt în total?
Putem efectua operațiunea astfel: total cărți = (3 x 5) x 8 = 15 x 8 = 120 cărți.
Sau așa: 3 x (5 x 8) = 3 x 40 = 120 de cărți.

Exemple
-În seturile de numere naturale, întregi, raționale, reale și complexe, proprietatea asociativă a adunării și multiplicării este îndeplinită.
-Pentru polinoame se aplică și în aceste operații.
-În cazurile operațiilor de scădere, divizare și exponențiere, proprietatea asociativă nu este îndeplinită nici în număr real, nici în polinoame.
-În cazul matricilor, proprietatea asociativă este valabilă pentru adunare și multiplicare, deși în acest din urmă caz, comutativitatea nu este îndeplinită. Aceasta înseamnă că, având în vedere matricile A, B și C, este adevărat că:
(A x B) x C = A x (B x C)
Dar ... A x B ≠ B x A
Proprietatea asociativă în vectori
Vectorii formează un set diferit de numerele reale sau numerele complexe. Operațiile definite pentru setul de vectori sunt oarecum diferite: există adunare, scădere și trei tipuri de produse.
Suma vectorilor îndeplinește proprietatea asociativă, la fel ca și numerele, polinoamele și matricile. În ceea ce privește produsele scalare, scalare cu vector și cruce realizate între vectori, acesta din urmă nu-l îndeplinește, dar produsul scalar, care este un alt tip de operație între vectori, îl îndeplinește, ținând cont de următoarele:
-Produsul unui scalar și al unui vector are ca rezultat un vector.
-Și atunci când înmulțiți doi vectori în mod scalar, rezultă un scalar.
Prin urmare, având în vedere vectorii v, sau Da w, și în plus un scalar λ, este posibil să scrieți:
-Suma de vectori: v +(sau + w ) = (v + sau) + w
-Produs scalar: λ (v • sau ) = (λv) • sau
Acesta din urmă este posibil datorită v • sau rezultă un scalar și λv este un vector.
In orice caz:
v × (sau × w ) ≠ (v × sau)×w
Factorizarea polinoamelor prin gruparea de termeni
Această aplicație este foarte interesantă, deoarece așa cum s-a spus anterior, proprietatea asociativă ajută la rezolvarea anumitor probleme. Suma monomiilor este asociativă și aceasta poate fi utilizată pentru a lua în considerare atunci când un factor comun evident nu apare la prima vedere.
De exemplu, să presupunem că cereți să luați în considerare: X3 + DouăXDouă + 3X +6. Acest polinom nu are un factor comun, dar să vedem ce se întâmplă dacă este grupat astfel:
X3 + 2xDouă + 3x +6 = (x3 + 2xDouă) + (3x +6)
Prima paranteză are ca factor comun XDouă:
X3 + DouăXDouă = XDouă (x + 2)
În al doilea factor comun este 3:
3x +6 = 3 (x + 2)
Atunci:
X3 + DouăXDouă + 3X +6 = XDouă(x + 2) + 3 (x + 2)
Acum există un factor comun evident, care este x + 2:
XDouă(x + 2) + 3 (x + 2) = (x + 2) (xDouă+3)
Instruire
- Exercitiul 1
O clădire școlară are 4 etaje și fiecare are 12 săli de clasă cu 30 de birouri în interior. Câte birouri are școala în total?
Soluţie
Această problemă este rezolvată prin aplicarea proprietății asociative a multiplicării, să vedem:
Număr total de birouri = 4 etaje x 12 săli de clasă / etaj x 30 de birouri / clasă = (4 x 12) x 30 de birouri = 48 x 30 = 1440 de birouri.
Sau, dacă preferați: 4 x (12 x 30) = 4 x 360 = 1440 de birouri
- Exercițiul 2
Având în vedere polinoamele:
A (x) = 5x3 + 2xDouă -7x + 1
B (x) = x4 +6x3 -5x
C (x) = -8xDouă +3x -7
Aplicați proprietatea asociativă a adunării pentru a găsi A (x) + B (x) + C (x).
Soluţie
Puteți grupa primele două și adăuga a treia la rezultat:
A (x) + B (x) = [5x3 + 2xDouă -7x + 1] + [x4 +6x3 -5x] = x4 + 11x3+ 2xDouă -12x +1
Imediat se adaugă polinomul C (x):
[X4 + 11x3+ 2xDouă -12x +1] + [-8xDouă +3x -7] = x4 + 11x3 - 6xDouă -9x -6
Cititorul poate verifica dacă rezultatul este identic dacă este rezolvat prin intermediul opțiunii A (x) + [B (x) + C (x)].
Referințe
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematica este distractivă. Legi comutative, asociative și distributive. Recuperat de pe: mathisfun.com.
- Depozit Math. Definiția proprietății asociative. Recuperat de pe: mathwarehouse.com.
- Știința. Proprietate asociativă și comutativă a adunării și multiplicării (cu exemple). Recuperat de pe: sciencing.com.
- Wikipedia. Proprietate asociativă. Recuperat de pe: en.wikipedia.org.



Nimeni nu a comentat acest articol încă.