
Explicația proporționalității compuse, regula compusă din trei, exerciții
proporționalitate compusă sau multiplă Este relația dintre mai mult de două magnitudini, unde proporționalitatea directă și inversă poate fi observată între date și necunoscut. Aceasta este o versiune mai avansată de proporționalitate simplă, deși tehnicile utilizate în ambele proceduri sunt similare..
De exemplu, dacă sunt necesare 7 persoane pentru a descărca 10 tone de marfă în 3 ore, proporționalitatea compusă poate fi utilizată pentru a calcula câte persoane va fi nevoie pentru a descărca 15 tone în 4 ore..
Pentru a răspunde la această întrebare, este convenabil să faceți un tabel de valori pentru a studia și a raporta magnitudinile și necunoscutele.
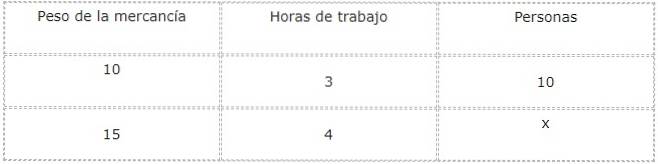
Continuăm să analizăm tipurile de relații dintre fiecare magnitudine și necunoscutul prezent, care pentru acest caz corespunde numărului de persoane care vor lucra.
Pe măsură ce crește greutatea mărfii, crește și numărul de persoane necesare pentru descărcare. Din această cauză, relația dintre greutate și lucrători este directă.
Pe de altă parte, odată cu creșterea numărului de lucrători, orele de lucru scad. Datorită acestui fapt, relația dintre oameni și orele de lucru este de tip invers.
Indice articol
- 1 Cum se calculează proporționalitățile compuse
- 2 Explicație
- 3 Regula directă a trei
- 4 Regula inversă a trei
- 5 Stare
- 6 Verificarea rezultatelor
- 7 Clearance
- 8 Istorie
- 9 Exerciții rezolvate
- 9.1 Exercițiul 1
- 9.2 Exercițiul 2
- 10 Exerciții propuse
- 11 Referințe
Cum se calculează proporționalitățile compuse
Pentru a rezolva exemple precum cel de mai sus, se utilizează în cea mai mare parte metoda regulii compuse din trei. Aceasta constă în stabilirea tipurilor de relații între magnitudini și necunoscute și apoi reprezentarea unui produs între fracțiuni.
În ceea ce privește exemplul inițial, fracțiile corespunzătoare tabelului de valori sunt organizate după cum urmează:
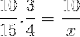
Dar înainte de a rezolva și rezolva necunoscutul, fracțiile corespunzătoare relației inverse trebuie inversate. Care pentru acest caz corespund timpului variabil. În acest fel, operațiunea de rezolvat va fi:
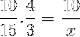
A cărei diferență este inversarea fracției corespunzătoare variabilei de timp 4/3. Continuăm să operăm și să ștergem valoarea lui x.
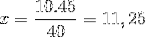
Astfel, sunt necesare peste unsprezece persoane pentru a putea descărca 15 tone de marfă în 4 ore sau mai puțin.
Explicaţie
Proporționalitatea este relația constantă dintre mărimile care pot fi modificate, care va fi simetrică pentru fiecare dintre cantitățile implicate. Există relații proporționale direct și invers, definind astfel parametrii proporționalității simple sau compuse.
Regula directă a trei
Acesta constă dintr-o relație de proporție între variabile, care prezintă același comportament atunci când sunt modificate. Este foarte frecvent în calculul procentelor referitoare la alte magnitudini decât o sută, unde este apreciată structura sa fundamentală.
De exemplu, se poate calcula 15% din 63. La prima vedere, acest procent nu poate fi ușor apreciat. Dar implementând regula celor trei, se poate face următoarea relație: dacă 100% este 63, atunci 15%, cât va fi?
100% - 63
15% -X
Iar operația corespunzătoare este:
(15%. 63) / 100% = 9,45
În cazul în care semnele procentuale sunt simplificate și se obține cifra 9.45, care reprezintă 15% din 63.
Regula inversă a trei
După cum indică și numele, în acest caz relația dintre variabile este opusă. Relația inversă trebuie stabilită înainte de a trece la calcul. Procedura sa este omologă cu cea a regulii directe a trei, cu excepția investiției în fracția de calculat..
De exemplu, 3 pictori au nevoie de 5 ore pentru a termina un perete. În câte ore l-ar termina 4 pictori?
În acest caz, relația este inversă, deoarece, odată cu creșterea numărului de pictori, timpul de lucru ar trebui să scadă. Relația este stabilită;
3 pictori - 5 ore
4 pictori- X ore
Pe măsură ce relația este inversată, ordinea de funcționare este inversată. Acesta fiind modul corect;
(3 pictori). (5 ore) / 4 pictori = 3,75 ore
Termenul de pictori este simplificat, iar rezultatul este de 3,75 ore.
Condiție
Pentru a fi în prezența unei proporționalități compuse sau multiple, este necesar să se găsească ambele tipuri de relații între magnitudini și variabile.
- Direct: Variabila are același comportament ca necunoscutul. Adică, atunci când unul crește sau scade, celălalt se modifică în mod egal.
- Invers: Variabila prezintă un comportament antonim față de cel al necunoscutului. Fracția care definește variabila menționată în tabelul de valori trebuie inversată, pentru a reprezenta relația invers proporțională între variabilă și necunoscută..
Verificarea rezultatelor
Este foarte obișnuit să se confunde ordinea mărimilor atunci când se lucrează cu proporționalități compuse, spre deosebire de ceea ce se întâmplă în calculele obișnuite ale proporției, a căror natură este în cea mai mare parte directă și rezolvabilă prin intermediul unei reguli simple de trei..
Din acest motiv, este important să se examineze ordinea logică a rezultatelor, verificând coerența figurilor produse de regula celor trei compuse.
În exemplul inițial, a face o astfel de greșeală ar avea ca rezultat 20. Adică 20 de persoane vor descărca 15 tone de marfă în 4 ore.
La prima vedere, nu pare un rezultat nebunesc, dar este curios o creștere de aproape 200% a personalului (de la 7 la 20 de persoane) atunci când creșterea mărfurilor este de 50% și chiar cu o marjă de timp mai mare desfășurați lucrarea.
În acest fel, verificarea logică a rezultatelor reprezintă un pas important în implementarea regulii celor trei compuși..
Clearance
Deși are o natură mai de bază în ceea ce privește pregătirea matematică, clearance-ul reprezintă un pas important în cazurile de proporționalitate. O degajare greșită este suficientă pentru a invalida orice rezultat obținut în regula simplă sau compusă din trei..
Poveste
Regula celor trei a devenit cunoscută în Occident prin intermediul arabilor, cu publicații ale diferiților autori. Printre ei Al-Jwarizmi și Al-Biruni.
Al-Biruni, datorită cunoștințelor sale multiculturale, a avut acces la vaste informații cu privire la această practică în călătoriile sale în India, fiind responsabil pentru cea mai extinsă documentație cu privire la regula celor trei.
El susține în cercetările sale că India a fost primul loc în care utilizarea regulii celor trei a devenit obișnuită. Scriitorul asigură că a fost realizat într-un mod fluid în versiunile sale directe, inverse și chiar compuse..
Data exactă când regula celor trei a devenit parte a cunoștințelor matematice din India este încă necunoscută. Cu toate acestea, cel mai vechi document care abordează această practică, manuscrisul Bakhshali, a fost descoperit în 1881. În prezent se află la Oxford.
Mulți istorici ai matematicii susțin că acest manuscris datează de la începutul erei prezente..
Exerciții rezolvate
Exercitiul 1
O companie aeriană trebuie să transporte 1.535 de persoane. Se știe că, cu 3 avioane, ar dura 12 zile pentru a ajunge ultimul pasager la destinație. Încă 450 de persoane au ajuns la compania aeriană și 2 avioane sunt ordonate să fie reparate pentru a ajuta la această sarcină. Câte zile va dura compania aeriană pentru a transfera ultimul pasager la destinație?
Relația dintre numărul de persoane și zilele de muncă este directă, deoarece cu cât numărul oamenilor este mai mare, cu atât vor dura mai multe zile pentru a realiza această muncă..
Pe de altă parte, relația dintre avioane și zile este invers proporțională. Pe măsură ce numărul avioanelor crește, zilele necesare pentru transferul tuturor pasagerilor scad.
Se realizează tabelul valorilor care se referă la acest caz.

Așa cum este detaliat în exemplul inițial, numeratorul și numitorul trebuie inversate în fracția corespunzătoare variabilei inverse în raport cu necunoscutul. Operația este următoarea:
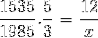
X = 71460/7675 = 9,31 zile
Pentru a transfera 1985 persoane folosind 5 avioane, este nevoie de mai mult de 9 zile.
Exercițiul 2
O recoltă de porumb de 25 de tone este dusă la camioanele de marfă. Se știe că anul precedent le-au luat 8 ore cu o salarizare de 150 de lucrători. Dacă pentru acest an salariul a crescut cu 35%, cât va dura până când va fi umplut camionul de marfă cu o recoltă de 40 de tone??
Înainte de a reprezenta tabelul valorilor, trebuie definit numărul de lucrători pentru acest an. Aceasta a crescut cu 35% față de cifra inițială de 150 de lucrători. Pentru aceasta se folosește o regulă directă de trei.
100% - 150
35% - X
X = (35.100) / 100 = 52,5. Acesta este numărul de lucrători suplimentari față de anul precedent, obținând un număr total de lucrători de 203, după rotunjirea sumei obținute.
Continuăm să definim tabelul de date corespunzător

Pentru acest caz, greutatea reprezintă o variabilă direct legată de timpul necunoscut. Pe de altă parte, variabila lucrătorilor are o relație inversă cu timpul. Cu cât numărul lucrătorilor este mai mare, cu atât ziua de lucru este mai scurtă.
Luând în considerare aceste considerații și inversând fracția corespunzătoare variabilei lucrătorilor, trecem la calcul.
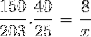
X = 40600/6000 = 6,76 ore
Ziua va dura puțin sub 7 ore.
Exerciții propuse
- Definiți 73% din 2875.
- Calculați numărul de ore pe care le doarme Teresa, dacă se știe că doarme doar 7% din total pentru ziua respectivă. Definiți câte ore dormiți pe săptămână.
- Un ziar publică 2000 de exemplare la fiecare 5 ore, folosind doar 2 aparate de tipărit. Câte exemplare va produce în 1 oră, dacă folosește 7 mașini? Cât timp va dura 10.000 de exemplare folosind 4 aparate?
Referințe
- Enciclopedia Alvarez-inițiere. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Manual complet de instrucțiuni primare elementare și superioare: pentru utilizarea profesorilor aspiranți și în special a studenților din Școlile Normale din provincie, Volumul 1. Joaquín Avendaño. Tipărirea lui D. Dionisio Hidalgo, 1844.
- Aproximarea rațională a funcțiilor reale. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mar. 2011.
- Aritmetica elementară pentru predarea în școli și colegii din America Centrală. Darío González. Bacsis. Arenales, 1926.
- Studiul matematicii: Despre studiul și dificultățile matematicii. Augustus De Morgan. Baldwin și Cradock, 1830.


Nimeni nu a comentat acest articol încă.