
Exemple de rapoarte trigonometrice, exerciții și aplicații
raporturi trigonometrice sunt coeficienții sau rapoartele care se pot face cu valoarea laturilor unui triunghi dreptunghiular. Aceste laturi sunt: două picioare care se formează la 90º între ele și hipotenuza, care formează unghiul acut θ cu una dintre picioare.
Puteți forma 6 coeficienți. Numele și abrevierile respective sunt:
- sân (sen)
- cosinus (cos)
- tangenta (tg sau tan)
- cotangent (ctg sau cotan)
- secant (sec) și
- cosecant (cosec)
Toate s-au referit la unghiul θ, așa cum se arată în figura următoare:
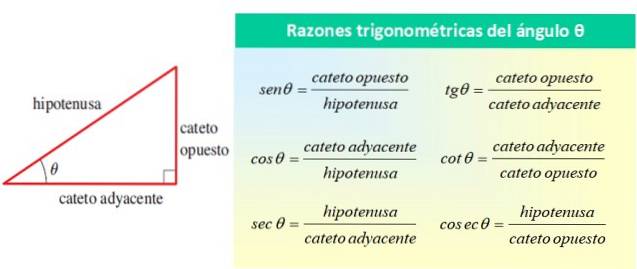
Raporturile trigonometrice de bază ale unghiului θ sunt sin θ, cos θ și tan θ, în timp ce raporturile rămase pot fi exprimate în termeni ai acestor trei. Din tabelul de mai sus se poate observa că:
- sec θ = 1 / cos θ
- cosec θ = 1 / sin θ
- pătuț θ = 1 / tg θ
Mărimea laturilor triunghiului nu influențează valoarea raporturilor, deoarece doi triunghiuri ale căror unghiuri măsoară la fel sunt triunghiuri similare, iar raporturile respective dintre laturi au aceeași valoare.
Indice articol
- 1 Exemplu
- 2 exerciții rezolvate
- 2.1 - Exercițiul 1
- 2.2 - Exercițiul 2
- 3 Aplicații ale raporturilor trigonometrice
- 4 Referințe
Exemplu
De exemplu, să calculăm raporturile trigonometrice ale unghiului θ în următoarele triunghiuri:
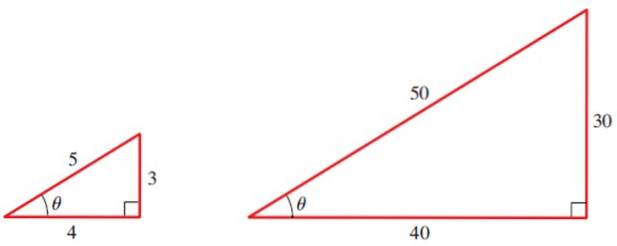
Pentru triunghiul mic avem cele trei rapoarte de bază ale unghiului θ:
păcatul θ = 3/5
cos θ = 4/5
tg θ = ¾
Și acum să calculăm cele trei rapoarte de bază ale lui θ cu triunghiul mare:
păcat θ = 30/50 = 3/5
cos θ = 40/50 = 4/5
tg θ = 30/40 = ¾
Un detaliu important de luat în considerare este următorul: atât sin θ, cât și cos θ sunt mai mici de 1, deoarece picioarele măsoară întotdeauna mai puțin decât hipotenuza. Într-adevăr:
sin θ = 3/5 = 0,6
cos θ = 4/5 = 0,8
Exerciții rezolvate
În exercițiile următoare vi se cere să rezolvați triunghiul dreptunghiular, ceea ce înseamnă să găsiți lungimea celor trei laturi și măsura unghiurilor sale interne, dintre care unul măsoară întotdeauna 90º.
Teorema lui Pitagora se aplică triunghiurilor dreptunghiulare și este foarte utilă atunci când sunt cunoscute două dintre laturi și trebuie determinată partea lipsă. Teorema merge așa:
IpotenuzăDouă = picior opusDouă + picior adiacentDouă
Putem verifica teorema lui Pitagora cu triunghiul mic din figura 2, ale cărui picioare sunt 3 și 4. Ordinea în care sunt luate picioarele nu contează. Aplicând teorema pe care o avem:
IpotenuzăDouă = 3Două + 4Două = 9 + 16 = 25
Prin urmare, hipotenuza este:
Hipotenuză = √25 = 5
- Exercitiul 1
Calculați raporturile trigonometrice ale unghiurilor prezentate în următoarele triunghiuri:

Solutie la
Acest triunghi este același ca în figura 3, dar ni se cer rapoartele trigonometrice ale celuilalt unghi acut, notat α. Afirmația nu oferă valoarea hipotenuzei, totuși, prin aplicarea teoremei lui Pitagora știm că merită 5.
Raporturile pot fi calculate direct din definiție, având grijă la selectarea piciorului care este opusul unghiului α a calcula sin α. Sa vedem:
- sin α = 4/5
- cos α = 3/5
- tg α = 4/3
- pătuț α = ¾
- sec α = 1 / (3/5) = 5/3
- cosec α = 1 / (4/5) = 5/4
Și, după cum putem vedea, valorile raporturilor trigonometrice au fost schimbate. Într-adevăr, α și θ sunt unghiuri complementare, ceea ce înseamnă că se adaugă până la 90º. În acest caz este adevărat că sin α = cos θ și așa mai departe din celelalte motive.
Soluția b
Să calculăm ipotenuza triunghiului folosind teorema lui Pitagora:
IpotenuzăDouă = 20Două + douăzeci și unuDouă = 841
√841 = 29
Atunci cele 6 rapoarte trigonometrice ale unghiului β sunt:
- sin β = 20/29
- cos β = 21/29
- tg β = 20/21
- pătuț β = 21/20
- sec β = 1 / (21/29) = 29/21
- cosec β = 1 / (20/29) = 20/29
- Exercițiul 2
a) Găsiți valoarea lui x în figură.
b) Calculați perimetrul celor 3 triunghiuri prezentate.
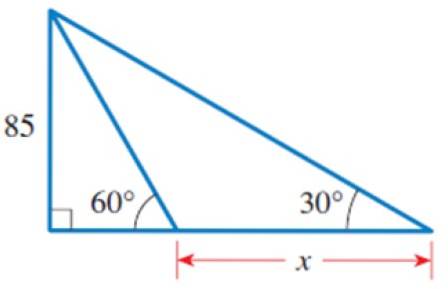
Solutie la
În figură putem identifica mai multe triunghiuri, în special triunghiul dreptunghiular din stânga, care are un picior egal cu 85 și unghiul acut 60º.
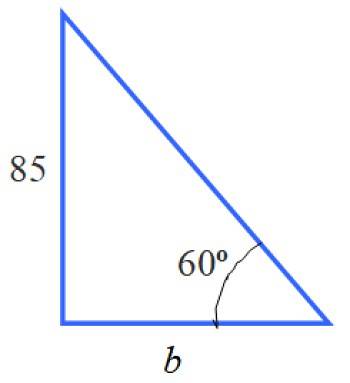
Cu informațiile din acest triunghi putem calcula latura b. Nu este măsura cerută de declarație, dar cunoașterea valorii acesteia este un pas anterior.
Pentru a determina acest lucru, raportul adecvat este tg 60º = 85 / b, deoarece b este piciorul adiacent la 60º și 85 este opusul unghiului menționat. Prin urmare:
b = 85 / tg 60º = 85 / √3
Odată ce b este cunoscut, vom folosi triunghiul drept și exterior exterior, care are o latură comună cu triunghiul anterior: cel care măsoară 85. Acesta este piciorul opus unghiului de 30º..
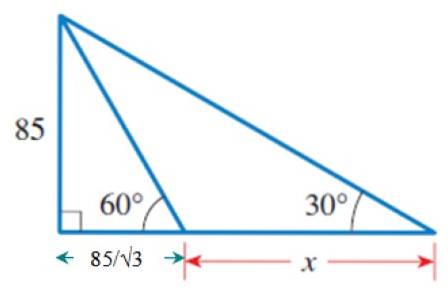
De acolo:
Picior adiacent la 30º = (85 / √3) + x
Acum putem propune următoarele:
85 / [(85 / √3) + x] = tg 30º
Ceea ce este între paranteze se întâmplă să înmulțească tg 30º:
85 = [(85 / √3) + x]. tg 30º
Aplicarea proprietății distributive a multiplicării:
85 = tg 30 °. (85 / √3) + x. tg 30º
Prin urmare:
x.tg 30º = 85 - tg 30º. (85 / √3) = 85 [1 - tg 30º. (1 / √3)] = 85. (2/3) = 170/3
Înlocuind valoarea tg 30º = √3 / 3:
x = (170/3) ÷ (√3 / 3) = 98,15
Soluția b
Perimetrul triunghiului mic
Să h1 hipotenuza acestui triunghi, care poate fi calculată prin teorema lui Pitagora sau prin intermediul unui raport trigonometric, de exemplu cos 60º:
cos 60 º = 85 / √3 / h1→ h1 = (85 / √3) ÷ cos 60º = 98,1
Pentru a găsi P, perimetrul acestui triunghi, adăugăm pur și simplu cele 3 laturi:
P = 85 + (85 / √3) + 98,1 = 232,2
Perimetrul triunghiului exterior
Să hDouă la ipotenuza triunghiului exterior:
sin 30º = 85 ÷ hDouă
hDouă = 85 ÷ sin 30º = 170
Pentru acest triunghi perimetrul este:
P = 85 + [(85 / √3) + 98,15] + 170 = 402,22
Perimetrul triunghiului non-drept
Știm deja toate laturile sale ale acestui triunghi:
P = x + h1 + hDouă = 98,15 + 98,15 + 170 = 366,3
Aplicații ale raporturilor trigonometrice
Rapoartele trigonometrice au numeroase aplicații practice, de exemplu pot fi calculate înălțimile.
Să presupunem că un turn de apă se află la 325 de metri de o clădire. Un observator la o fereastră observă că unghiul de înălțime al capătului superior al turnului este de 39º, în timp ce unghiul de depresiune cu care este privită baza turnului este de 25º. Se intreaba:
a) Care este înălțimea turnului?
b) Cât de înaltă este fereastra?
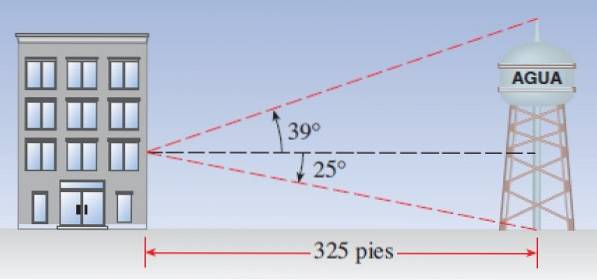
Solutie la
Din piciorul opus 39 ° al triunghiului superior obținem o parte a răspunsului:
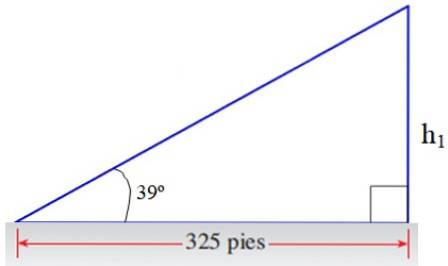
h1/ 325 = tg 39º → h1 = 325. tg 39º picioare = 263,2 picioare
În mod similar obținem restul înălțimii turnului, numit hDouă pornind de la triunghiul inferior:
hDouă/ 325 = tg 25º → hDouă = 325. tg 25º picioare = 151,6 picioare
Înălțimea totală a turnului este de h1 + hDouă = 263,2 + 151,6 picioare = 414,7 picioare.
Soluția b
Fereastra este exact la o înălțime hDouă sol:
hDouă = 151,6 picioare.
Referințe
- Carena, M. 2019. Manual pre-universitar de matematică. Universitatea Națională a Litoralului.
- Hoffman, J. Selecția subiectelor de matematică. Volumul 3.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalcul: Matematică pentru calcul. Al 5-lea. Ediție. Cengage Learning.
- Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.



Nimeni nu a comentat acest articol încă.