
Conceptul de rețele Bravais, caracteristici, exemple, exerciții
Plase Bravais Acestea sunt ansamblul a paisprezece celule unitare tridimensionale în care pot fi localizați atomii unui cristal. Aceste celule constau dintr-o dispunere tridimensională a punctelor care formează o structură de bază care se repetă periodic în cele trei direcții spațiale..
Originea acestei denumiri pentru structurile cristaline de bază vine din 1850, când Auguste Bravais a arătat că există doar 14 celule tridimensionale posibile ale unității de bază.

Setul de 14 rețele Bravais este împărțit în șapte grupuri sau structuri în funcție de geometria celulelor, aceste șapte grupuri sunt:
1- Cubic
2- Tetragonal
3- Orthorhombic
4- Trigonal-Hexagonal
5- Monoclinic
6- Triclinic
7- Trigonal
Fiecare dintre aceste structuri definește o celulă unitară, aceasta fiind cea mai mică porțiune care păstrează dispunerea geometrică a atomilor din cristal..
Indice articol
- 1 Caracteristicile rețelelor Bravais
- 1.1 Rețele cubice
- 2 Exemple
- 2.1 - Fier
- 2.2 - Cupru
- 2.3 - Pietre prețioase
- 2.4 Topaz
- 3 exerciții rezolvate
- 3.1 Exercițiul 1
- 3.2 Exercițiul 2
- 3.3 Exercițiul 3
- 4 Referințe
Caracteristicile rețelelor Bravais
Cele paisprezece rețele Bravais, așa cum am menționat mai sus, sunt împărțite în șapte grupuri. Dar fiecare dintre aceste grupuri are celulele sale unitare cu parametrii caracteristici care sunt:
1- Parametrul de rețea (a, b, c)
2- Numărul de atomi pe celulă
3- Relația dintre parametrul de rețea și raza atomică
4- Numărul de coordonare
5- Factorul de ambalare
6- spații interstițiale
7- Prin traduceri de-a lungul vectorilor a, b, c se repetă structura cristalină.
Rețele cubice
Se compune din rețeaua cubică simplă sau cubică P, rețeaua cubică centrată pe față sau rețeaua cubică F și rețeaua cubică centrată pe corp sau rețeaua cubică I.
Toate rețelele cubice le au pe toate parametrii rețelei corespunzând direcțiilor x, y, z de aceeași valoare:
a = b = c
Rețea cubică P
Trebuie remarcat faptul că atomii sunt reprezentați de sfere ale căror centre se află la vârfurile celulei unității cubice P.
În cazul rețelei cubice P numărul de atomi pe celulă este 1, deoarece la fiecare vârf doar o optime din atom se află în interiorul celulei unitare, deci 8 * ⅛ = 1.
număr de coordonare indică numărul de atomi care sunt vecini apropiați în rețeaua de cristal. În cazul rețelei cubice P, numărul de coordonare este 6.
Rețea cubică I
În acest tip de rețea, pe lângă atomii de la vârfurile cubului, există un atom în centrul cubului. Asa ca numărul atomului pe celulă unitatea în rețea cubică P este de 2 atomi.

Rețea cubică F
Rețeaua cubică este cea care, pe lângă atomii din vârfuri, are un atom în centrul feței fiecărui cub. numărul de atomi pe celulă este 4, deoarece fiecare dintre cei șase atomi ai feței are jumătate în interiorul celulei, adică 6 * ½ = 3 plus 8 * ⅛ = 1 la vârfuri.

Plasa hexagonala
În acest caz, celula unitară este o prismă dreaptă cu o bază hexagonală. Rețelele hexagonale au toate cele trei parametrii rețelei corespondent care îndeplinește următoarea relație:
a = b ≠ c
Unghiul dintre vectorii a și b fiind de 120 °, așa cum se arată în figură. În timp ce între vectorii a și c, precum și între b și c, se formează unghiuri drepte.

numărul de atomi pe celulă va fi calculat după cum urmează:
- În fiecare dintre cele 2 baze ale prismei hexagonale există 6 atomi la cele șase vârfuri. Fiecare dintre acești atomi ocupă ⅙ din celula unitară.
- În centrul fiecăreia dintre cele 2 baze hexagonale există un atom care ocupă 1/2 unitate de celulă.
- Pe cele 6 fețe laterale ale prismei hexagonale există 3 atomi care ocupă fiecare ⅔ din celula unității și fiecare 3 atomi ocupă ⅓ din volumul celulei unitare.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
Relația dintre parametrii de rețea a și b cu raza atomică R, în ipoteza că toți atomii sunt de rază egală și sunt în contact este:
a / R = b / R = 2
Exemple
Metalele sunt principalele exemple de structuri cristaline și, de asemenea, cele mai simple, deoarece acestea constau în general dintr-un singur tip de atom. Dar există și alți compuși nemetalici care formează și structuri cristaline, precum diamantul, cuarțul și mulți alții..
- Fierul
Fierul are o singură celulă cubică cu parametru de rețea sau margine a = 0,297 nm. În 1 mm există 3,48 x 10 ^ 6 celule unitare.
- Cupru
Are o structură cristalină cubică centrată pe față, formată exclusiv din atomi de cupru..
- Pietre prețioase
Pietrele prețioase sunt structuri cristaline cu același compus, dar cu porțiuni mici de impurități care sunt adesea responsabile de culoarea lor..
Diamant
Este compus exclusiv din carbon și nu conține impurități, motiv pentru care este incolor. Diamantul are structură cristalină cubică (izometric-hexoctaedric) și este cel mai greu material cunoscut.
Cuarţ
Este compus din oxid de silice, este în general incolor sau alb. Structura sa cristalină este trigonal-trapezoedrică.
Rubin
Este compus din oxid de aluminiu cu impurități de crom care îi conferă culoarea roșie caracteristică. Formați un zăbrele de cristal hexagonale.
Safir
Este, de asemenea, un cristal de oxid de aluminiu, dar cu impurități de titan și fier, care sunt responsabile pentru culoarea sa albastră în diferite nuanțe. La fel ca rubinul structură hexagonală.
Jad
Piatră prețioasă, în general, de culoare verde, are structura monoclinică și este compus din silicat de fier-magneziu-calciu.
Topaz
Este incolor cu un structură ortorombică fluorură de aluminiu-hidroxid-silicat.
Exerciții rezolvate
Exercitiul 1
Găsiți relația dintre parametrul rețelei și raza atomică pentru o rețea cubică F.
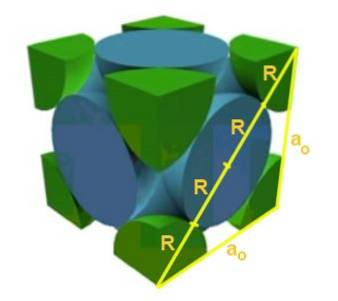
Soluţie: În primul rând, se presupune că atomii sunt reprezentați ca sfere cu rază R în „contact” unul cu celălalt, așa cum se arată în figură. Se formează un triunghi dreptunghiular în care este adevărat că:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Prin urmare, relația muchie-rază este:
a / R = 4 / √2
Exercițiul 2
Găsiți relația dintre parametrul rețelei și raza atomică pentru o rețea cubică I (centrată pe corp).
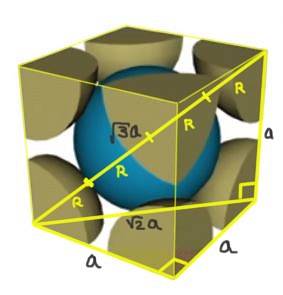
Soluţie: Se presupune că atomii sunt reprezentați ca sferele de toate razele R în „contact” unul cu celălalt, așa cum se arată în figură.
Se formează două triunghiuri dreptunghiulare, unul de hipotenuză √2a și celălalt de hipotenuză √3a, după cum se poate demonstra folosind teorema lui Pitagora. De aici rezultă că relația dintre parametrul rețelei și raza atomică pentru o rețea cubică I (centrată în corp) este:
a / R = 4 / √3
Exercițiul 3
Găsiți factorul de ambalare F pentru o celulă unitară a unei structuri cubice F (cubic centrat pe față) în care atomii au raza R și sunt în „contact”.
Soluţie: Factorul de ambalare F este definit ca coeficientul dintre volumul ocupat de atomii din celula unității și volumul celulei:
F = Vatomi / Vcelulă
După cum s-a demonstrat mai sus, numărul de atomi pe unitate de celulă într-o rețea cubică centrată pe față este de 4, deci factorul de ambalare va fi:
F = 4 [4πR ^ 3/3] / [a ^ 3] = ...
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Referințe
- Centrul de Resurse Academice Structuri de Cristal. [PDF]. Adus pe 24 mai 2018, de pe: web.iit.edu
- Cristale. Adus pe 26 mai 2018, de pe: thoughtco.com
- Caiete de presă. 10.6 Structuri de rețea în solide cristaline. Adus pe 26 mai 2018, de pe: opentextbc.ca
- Ming. (2015, 30 iunie). Tipuri Structuri de cristal. Adus pe 26 mai 2018, de pe: crystalvisions-film.com
- Helmenstine, Anne Marie, dr. (31 ianuarie 2018). Tipuri de
- Kittel Charles (2013) Fizica stării solide, fizica materiei condensate (ediția a VIII-a). Wiley.
- KHI. (2007). Structuri cristaline. Adus pe 26 mai 2018, de pe: folk.ntnu.no
- Wikipedia. Grile Bravais. Recuperat de pe: en.wikipedia.com.

Nimeni nu a comentat acest articol încă.