
A doua explicație a condiției de echilibru, exemple, exerciții
a doua condiție de echilibru stabilește că suma cuplurilor sau momentelor produse de toate forțele care acționează asupra unui corp, indiferent de punctul în care sunt calculate, trebuie anulată, astfel încât respectivul corp să fie în echilibru static sau dinamic.
Notând cuplul sau momentul forței prin litera greacă τ, matematic se exprimă astfel:
∑ τ = 0

Litera aldinată indică natura vectorială a momentului, care trebuie anulată în raport cu orice punct ales ca centru de rotație. În acest fel, anularea cuplului net asigură faptul că obiectul nu începe să se rotească sau să se răstoarne..
Cu toate acestea, dacă obiectul se rotea deja anterior și cuplul net dispare brusc, rotația va continua, dar cu viteză unghiulară constantă.
Cea de-a doua condiție de echilibru este utilizată împreună cu prima condiție, care spune că suma forțelor pe un corp trebuie să fie zero, astfel încât să nu se traducă sau că, dacă se întâmplă, este cu o mișcare rectilinie uniformă:
∑ F = 0
Ambele condiții se aplică corpurilor extinse, ale căror dimensiuni sunt măsurabile. Când se presupune că un obiect este o particulă, nu are sens să vorbim despre rotații, iar prima condiție este suficientă pentru a garanta echilibrul.
Exemple
A doua condiție de echilibru este dezvăluită în nenumărate situații:
Pe măsură ce urci scara
Când susținem o scară pe podea și pe perete, avem nevoie de suficientă frecare, mai ales pe podea, pentru a ne asigura că scara nu alunecă. Dacă încercăm să urcăm pe o scară sprijinită pe o podea uleioasă, umedă sau alunecoasă, nu este dificil să anticipăm că vom cădea.
Pentru a putea folosi scara cu încredere, este necesar ca acesta să fie în echilibru static în timp ce urcați și când se află pe treapta necesară.
Mutarea unui dulap
Când doriți să mutați o piesă de mobilier înaltă, cum ar fi un dulap sau orice piesă a cărei înălțime este mai mare decât lățimea sa, este convenabil să împingeți pe un punct scăzut, pentru a evita răsturnarea, în acest fel este mai probabil ca mobilierul va aluneca în loc să se întoarcă și se va întinde.
În astfel de circumstanțe, mobilierul nu este neapărat în echilibru, deoarece s-ar putea mișca rapid, dar cel puțin nu s-ar răsturna.
Balcoane
Balcoanele care ies din clădiri ar trebui construite asigurându-se că, chiar dacă sunt mulți oameni deasupra, nu se răstoarnă și se prăbușește.
Dielectric în câmpuri electrice externe
Prin plasarea unui material dielectric într-un câmp electric extern, moleculele se mișcă și se rotesc până când adoptă o poziție de echilibru, creând un câmp electric în interiorul materialului..
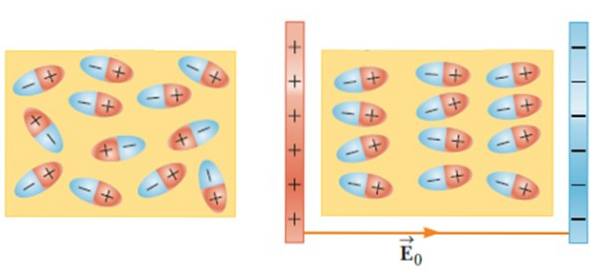
Acest efect crește capacitatea unui condensator atunci când un material precum sticlă, cauciuc, hârtie sau ulei este introdus între cadre..
Semne și lămpi
Este obișnuit ca mulți localnici să atârne anunțuri pe peretele clădirii, astfel încât să fie vizibile pentru trecători.
Afișul este ținut de o bară și un cablu, ambele fixate pe perete de paranteze. Diferitele forțe care acționează trebuie să se asigure că posterul nu cade, pentru care intră în joc cele două condiții de echilibru.
Un reflector poate fi, de asemenea, așezat într-un parc, ca în figura următoare:
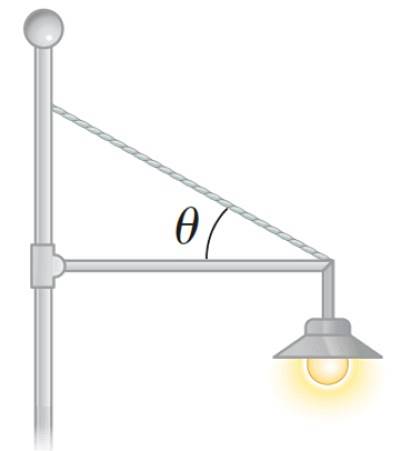
Cum se calculează cuplul net sau momentul net al unei forțe?
Cuplul sau momentul unei forțe, notat cu τ sau M în unele texte, este întotdeauna calculat în raport cu un punct în care trece axa de rotație.
Este definit ca produsul vectorial între vectorul de poziție r, care este direcționat de la axa menționată la punctul de aplicare a forței și forței F:
τ = r × F
Fiind un vector, este necesar să se exprime cuplul, dându-i amploarea, direcția și simțul. Magnitudinea este dată de:
τ = rF.sen θ
Regula mâinii drepte pentru produsul vector
Când problema este în plan, direcția cuplului este perpendiculară pe hârtie sau ecran, iar direcția este determinată de regula din dreapta, în care degetul arătător îndreaptă spre r, degetul mijlociu spre F iar degetul mare indică în sau în afara hârtiei.
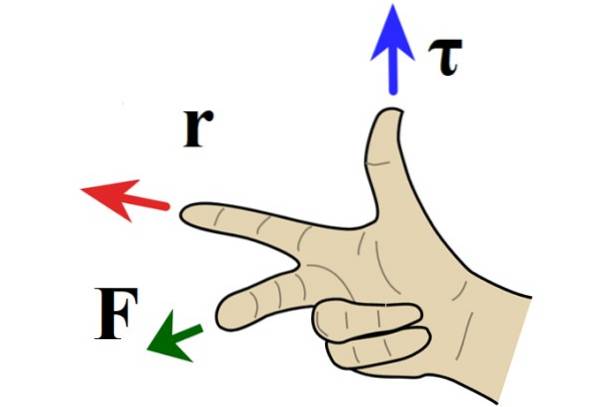
Când cuplul indică hârtia, rotația este în sens invers acelor de ceasornic și i se atribuie un semn pozitiv prin convenție. Dacă în schimb cuplul este îndreptat spre interiorul lamei, rotația este în sensul acelor de ceasornic și negativă..
Pentru a găsi cuplul net, se alege un punct convenabil pentru calcul, care poate fi cel la care acționează cea mai mare cantitate de forțe. În acest caz, momentul acestor forțe este zero, deoarece are un vector de poziție r de magnitudine 0.
Puteți alege orice punct care oferă suficiente informații pentru a rezolva necunoscutul care solicită rezolvarea problemei. Să vedem mai detaliat mai jos.
Exercițiul a fost rezolvat
Reflectorul din figura următoare are o masă de 20 kg și este susținut de o bară orizontală subțire, de masă și lungime L neglijabilă, care este articulată pe un stâlp. Cablul, de asemenea ușor, care ajută la susținerea reflectorului, formează un unghi θ = 30º cu bara. Calculati:
a) Tensiunea din cablu
b) Mărimea forței F pe care stâlpul o exercită asupra barei prin balama.
Soluţie
Vom aplica prima condiție de echilibru ∑ F = 0 la forțele prezentate în diagramă:
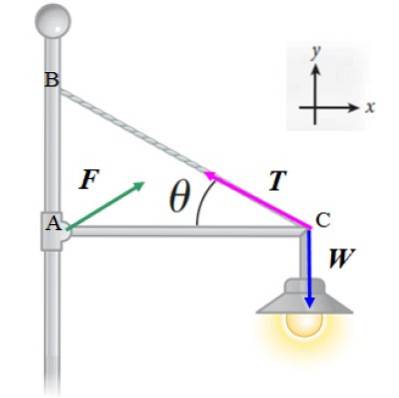
F + T + W = 0
Rețineți că magnitudinea și direcția F sunt încă de stabilit, dar presupunem că are două componente: FX și FDa. În acest fel obținem două ecuații:
FX -T. cos θ = 0
FDa - W + T⋅ sin θ = 0
Acum să aplicăm a doua condiție de echilibru, alegând punctul A, deoarece nu cunoaștem magnitudinea F nici cea a T. Alegând acest punct, vectorul rLA este nul, deci momentul F este nulă și magnitudinea F nu va apărea în ecuație:
-W⋅L + T⋅sen θ⋅L = 0
Prin urmare:
T.sen θ.L = W.L
T = L / sin θ = (20 kg x 9,8 m / sDouă) / Sin 30º = 392 N
Cunoscând magnitudinea lui T putem rezolva pentru componenta FX:
FX = T⋅ cos θ = 392 cos 30º N = 339. 5 N
Și apoi componenta FDa:
FDa = W - T⋅ sin θ = (20 kg x 9,8 m / sDouă) - 392⋅sin 30º = 0
Atunci putem exprima F Asa de:
F = 339,5 N X
Prin urmare, este o forță orizontală. Acest lucru se datorează faptului că am considerat că bara avea o greutate neglijabilă.
Dacă s-a ales punctul C pentru a calcula momentul rezultat, vectorii rT Da rW sunt nule, prin urmare:
M = FșiL = 0
Se concluzionează că FDa = 0. În acest fel:
- W + T⋅ sin θ = 0
T = W / sin θ
Care este același rezultat obținut inițial la alegerea punctului A ca locul pe care trece axa de rotație.
Teme de interes
Condiții de echilibru.
Prima condiție de echilibru.
Referințe
- Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 4. Sisteme de particule. Editat de Douglas Figueroa (USB).
- Giancoli, D. 2006. Fizică: principii cu aplicații. Al 6-lea. Ed prentice hall.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ed. Cengage Learning.



Nimeni nu a comentat acest articol încă.