
Teoria seturilor caracteristice, elemente, exemple, exerciții
teoria mulțimilor Este o ramură a logicii-matematicii care este responsabilă de studiul relațiilor dintre entități numite mulțimi. Seturile se caracterizează prin a fi colecții de obiecte de aceeași natură. Aceste obiecte sunt elementele setului și pot fi: cifre, litere, figuri geometrice, cuvinte care reprezintă obiecte, obiectele în sine și altele.
Georg Cantor, spre sfârșitul secolului al XIX-lea, a propus teoria mulțimilor. În timp ce alți matematicieni notabili din secolul al XX-lea și-au făcut formalizarea: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel printre alții..

Diagramele Venn sunt modalitatea grafică de a reprezenta o mulțime și constă dintr-o figură plană închisă în interiorul căreia sunt elementele mulțimii.
De exemplu, în figura 1 sunt prezentate două mulțimi A și B, care au elemente comune, elementele comune lui A și B. Acestea formează un nou set numit mulțimea de intersecție a lui A și B, care este scris în formă simbolică ca urmează:
A ∩ B
Indice articol
- 1 Caracteristici
- 2 Tipuri de seturi
- 2.1 Set finit
- 2.2 Set infinit
- 2.3 Set gol
- 2.4 Set unitar
- 2.5 Set binar
- 2.6 Set universal
- 3 Elemente de bază
- 3.1 - Relațiile dintre mulțimi
- 3.2 - Proprietățile incluziunii
- 3.3 - Operațiuni între seturi
- 4 Exemple
- 4.1 Exemplul 1
- 4.2 Exemplul 2
- 4.3 Exemplul 3
- 4.4 Exemplul 4
- 4.5 Exemplul 5
- 5 Exerciții rezolvate
- 5.1 Exercițiul 1
- 5.2 Exercițiul 2
- 5.3 Exercițiul 3
- 5.4 Exercițiul 4
- 6 Referințe
Caracteristici
Setul este un concept primitiv așa cum este în geometrie conceptul de punct, linie sau plan. Nu există o modalitate mai bună de a exprima conceptul decât indicând exemple:
Setul E format din culorile steagului Spaniei. Acest mod de exprimare a setului este numit prin înțelegere. Același set E scris prin extensie este:
E = roșu, galben
În acest caz, roșul și galbenul sunt elemente ale mulțimii E. Trebuie remarcat faptul că elementele sunt listate între paranteze și nu se repetă. În cazul steagului spaniol există trei dungi colorate (roșu, galben, roșu), dintre care două se repetă, dar elementele nu se repetă atunci când setul este exprimat..
Să presupunem că mulțimea V formată din primele trei litere vocale:
V = a, e, i
Setul de putere al lui V, notat cu P (V) este ansamblul tuturor seturilor care pot fi formate cu elementele lui V:
P (V) = a, e, i, a, e, a, i, e, i, a, e, i
Tipuri de seturi
Set finit
Este un set în care elementele sale sunt numărabile. Exemple de mulțimi finite sunt literele alfabetului spaniol, vocalele spaniolei, planetele sistemului solar, printre altele. Numărul de elemente ale unei mulțimi finite se numește cardinalitate.
Set infinit
Un set infinit este înțeles ca fiind tot ceea ce numărul elementelor sale este de nenumărat, deoarece oricât de mare ar fi numărul elementelor sale, este întotdeauna posibil să găsești mai multe elemente.
Un exemplu de mulțime infinită este mulțimea numerelor naturale N, care în formă extinsă este exprimată după cum urmează:
N = 1, 2, 3, 4, 5,…. Este clar un set infinit, deoarece oricât de mare ar fi un număr natural, următorul cel mai mare poate fi întotdeauna găsit, într-un proces nesfârșit. În mod clar, cardinalitatea unui set infinit este ∞.
Set gol
Este mulțimea care nu conține niciun element. Setul gol V este notat cu Ø sau cu o pereche de chei fără elemente în interior:
V = = Ø.
Setul gol este unic, de aceea trebuie să fie incorect să spui „un set gol”, forma corectă este să spui „setul gol”.
Printre proprietățile setului gol avem că este un subset al oricărui set:
Ø ⊂ A
Mai mult, dacă un set este un subset al setului gol, atunci neapărat setul respectiv va fi vidul:
A ⊂ Ø ⇔ A = Ø
Set unitar
Un set de unități este orice set care conține un singur element. De exemplu, setul de sateliți naturali ai Pământului este un set unitar, al cărui singur element este Luna. Mulțimea B de numere întregi mai mici de 2 și mai mari decât zero are doar elementul 1, prin urmare este o mulțime unitară.
Set binar
Un set este binar dacă are doar două elemente. De exemplu, mulțimea X, astfel încât x este o soluție de număr real de x ^ 2 = 2. Acest set prin extensie este scris astfel:
X = -√2, + √2
Set universal
Setul universal este un set care conține alte seturi de același tip sau natură. De exemplu, mulțimea universală a numerelor naturale este mulțimea numerelor reale. Dar numerele reale sunt un set universal și al numerelor întregi și al numerelor raționale.
Articole de bază
- Relațiile dintre mulțimi
În ansambluri, pot fi stabilite diferite tipuri de relații între ele și elementele lor. Dacă două mulțimi A și B au exact aceleași elemente între ele, se stabilește o relație de egalitate, notată după cum urmează:
LA = B
Dacă toate elementele unei mulțimi A aparțin unei mulțimi B, dar nu toate elementele lui B aparțin lui A, atunci între aceste mulțimi există o relație de incluziune care este notată astfel:
A ⊂ B, dar B ⊄ A
Expresia de mai sus spune: A este un subset al lui B, dar B nu este un subset al lui A.
Pentru a indica faptul că unele sau unele elemente aparțin unui set, se folosește simbolul de apartenență example, de exemplu pentru a spune că elementul sau elementele x aparțin setului A este scris simbolic astfel:
x ∈ A
Dacă un element nu aparține mulțimii A, această relație este scrisă astfel:
și ∉ A
Relația de membru apare între elementele unui set și set, cu singura excepție a setului de putere, setul de putere fiind colecția sau setul tuturor seturilor posibile care pot fi formate cu elementele setului menționat.
Să presupunem că V = a, e, i, setul său de putere este P (V) = a, e, i, a, e, a, i, e, i , a, e, i, în acest caz mulțimea V devine un element al mulțimii P (V) și poate fi scrisă:
V ∈ P (V)
- Proprietăți de incluziune
Prima proprietate a incluziunii stabilește că fiecare set este conținut în sine, sau cu alte cuvinte, că este un subset al său:
A ⊂ A
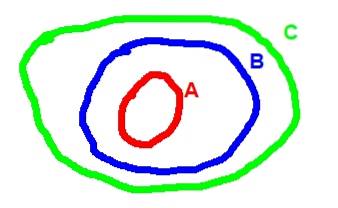
Cealaltă proprietate a incluziunii este tranzitivitatea: dacă A este un subset al lui B și B la rândul său este un subset al lui C, atunci A este un subset al lui C. În formă simbolică, relația de tranzitivitate se scrie după cum urmează:
(A ⊂ B) ^ (B ⊂ C) => A ⊂ C
Mai jos este diagrama Venn corespunzătoare tranzitivității incluziunii:
- Operații între seturi
Intersecție
Intersecția este o operație între două mulțimi care dă naștere la o nouă mulțime aparținând aceluiași set universal ca primele două. În acest sens, este o operațiune închisă.
Simbolic, operația de intersecție este formulată astfel:
A⋂B = x / x∈A ^ x∈B
Un exemplu este următorul: setul A al literelor din cuvântul „elemente” și setul B al literelor cuvântului „repetate”, intersecția dintre A și B este scrisă astfel:
A⋂B = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s. Setul universal U al lui A, al lui B și, de asemenea, al lui A⋂B este ansamblul literelor alfabetului spaniol.
Uniune
Unirea a două mulțimi este mulțimea formată din elementele comune celor două mulțimi și elementele necomune ale celor două mulțimi. Operațiunea de unire între seturi este exprimată simbolic astfel:
A∪B = x / x∈A v x∈B
Diferență
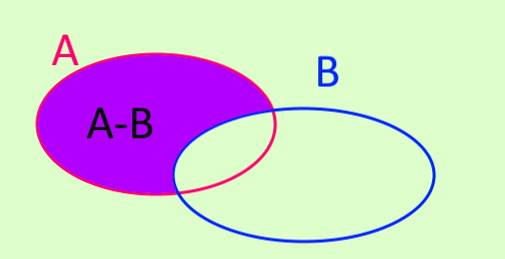
Operația diferențială a mulțimii A minus mulțimea B este notată cu A-B. A-B este un set nou format din toate elementele care se află în A și care nu aparțin lui B. Simbolic este scris astfel:
A - B = x / x ∈ A ^ x ∉ B
Diferență simetrică
Diferența simetrică este o operație între două mulțimi în care mulțimea rezultată este alcătuită din elementele care nu sunt comune celor două mulțimi. Diferența simetrică este reprezentată simbolic astfel:
A⊕B = x / x∈ (A-B) ^ x∈ (B-A)
Exemple
Exemplul 1
Diagrama Venn este un mod grafic de reprezentare a mulțimilor. De exemplu, setul C al literelor din setul de cuvinte este reprezentat astfel:

Exemplul 2
Se arată mai jos prin diagramele Venn că setul de vocale din cuvântul „set” este un subset al setului de litere din cuvântul „set”.

Exemplul 3
A stabilit Ñ dintre literele alfabetului spaniol este un set finit, acest set prin extensie este scris astfel:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z și cardinalitatea sa este 27.
Exemplul 4
A stabilit V dintre vocale în spaniolă este un subset al mulțimii Ñ:
V ⊂ Ñ de aceea este un set finit.
Mulțimea finită V în formă extinsă este scris astfel: V = a, e, i, o, u și cardinalitatea sa este 5.
Exemplul 5
Având în vedere mulțimile A = 2, 4, 6, 8 și B = 1, 2, 4, 7, 9 determinați A-B și B-A.
A - B sunt elementele lui A care nu sunt în B:
A - B = 6, 8
B - A sunt elementele lui B care nu se află în A:
B - A = 1, 7, 9
Exerciții rezolvate
Exercitiul 1
Scrieți în formă simbolică și, de asemenea, prin extensie, setul P al numerelor pare naturale mai mici de 10.
Soluţie: P = x∈ N / x < 10 ^ x mod 2 = 0
P = 2, 4, 6, 8
Exercițiul 2
Să presupunem că mulțimea A formată din numerele naturale care sunt factori de 210 și mulțimea B care se formează din numerele naturale prime mai mici de 9. Determinați prin extensie ambele mulțimi și stabiliți ce relație există între cele două mulțimi.
Soluţie: Pentru a determina elementele mulțimii A, trebuie să începem prin a găsi factorii numărului natural 210:
210 = 2 * 3 * 5 * 7
Apoi mulțimea A este scrisă:
A = 2, 3, 5, 7
Acum considerăm mulțimea B, care este primele mai mici de 9. 1 nu este prim, deoarece nu îndeplinește definiția primului: „un număr este prim dacă și numai dacă are exact doi divizori, 1 și numărul în sine” . 2 este egal și în același timp este prim, deoarece îndeplinește definiția unui prim, celelalte prime mai mici de 9 sunt 3, 5 și 7. Deci, mulțimea B este:
B = 2, 3, 5, 7
Prin urmare, cele două seturi sunt egale: A = B.
Exercițiul 3
Determinați mulțimea ale cărei elemente x sunt diferite de x.
Soluţie: C = x / x ≠ x
Deoarece fiecare element, număr sau obiect este egal cu el însuși, setul C nu poate fi altul decât setul gol:
C = Ø
Exercițiul 4
Fie mulțimea lui N a numerelor naturale și Z a fi mulțimea numerelor întregi. Determinați N ⋂ Z și N ∪ Z.
Soluţie:
N ⋂ Z = x ∈ Z / x ≤ 0 = (-∞, 0]
N ∪ Z = Z deoarece N ⊂ Z.
Referințe
- Garo, M. (2014). Matematică: ecuații pătratice: Cum se rezolvă o ecuație pătratică. Marilù Garo.
- Haeussler, E. F. și Paul, R. S. (2003). Matematică pentru management și economie. Pearson Education.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matematică 1 SEP. Prag.
- Preciado, C. T. (2005). Curs de matematică 3. Editorial Progreso.
- Matematică 10 (2018). „Exemple de seturi finite”. Recuperat de la: matematicas10.net
- Wikipedia. Teoria mulțimilor. Recuperat de pe: es.wikipedia.com


Nimeni nu a comentat acest articol încă.