Ecuația teoremei lui Bernoulli, aplicații și exerciții rezolvate

Teorema lui Bernoulli, care descrie comportamentul unui lichid în mișcare, a fost enunțat de matematicianul și fizicianul Daniel Bernoulli în lucrarea sa Hidrodinamică. Conform principiului, un fluid ideal (fără frecare sau vâscozitate) care circulă printr-o conductă închisă, va avea o energie constantă în calea sa.

Teorema poate fi dedusă din principiul conservării energiei și chiar din a doua lege a mișcării lui Newton. În plus, principiul lui Bernoulli stabilește, de asemenea, că o creștere a vitezei unui fluid implică o scădere a presiunii la care este supus, o scădere a energiei sale potențiale sau ambele în același timp..

Teorema are multe aplicații diferite, atât în ​​lumea științei, cât și în viața de zi cu zi a oamenilor..

Consecințele sale sunt prezente în forța de ridicare a avioanelor, în hornurile caselor și industriilor, în conductele de apă, printre alte zone..

Indice articol

• 1 Ecuația lui Bernoulli
  • 1.1 Formă simplificată
• 2 Aplicații
• 3 Exercițiul a fost rezolvat
• 4 Referințe

Ecuația lui Bernoulli

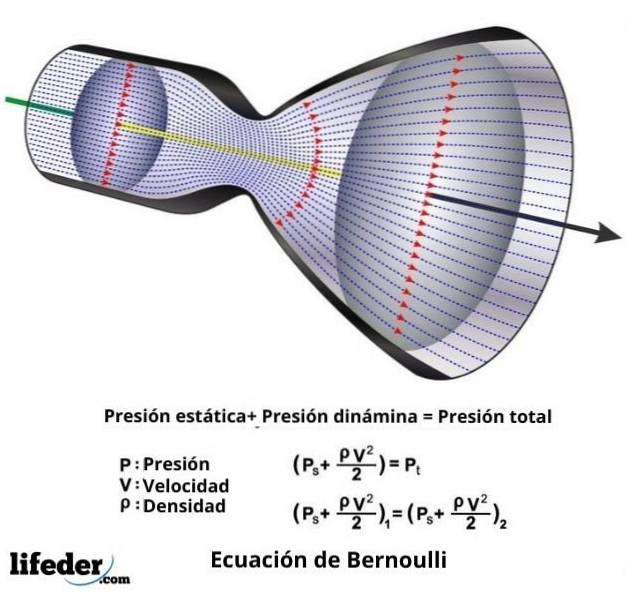
Deși Bernoulli a fost cel care a dedus că presiunea scade atunci când viteza de curgere crește, adevărul este că Leonhard Euler a dezvoltat de fapt ecuația Bernoulli în forma în care este cunoscută astăzi..

În orice caz, ecuația lui Bernoulli, care nu este altceva decât expresia matematică a teoremei sale, este următoarea:

v^Două ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = constantă

În această expresie, v este viteza fluidului prin secțiunea luată în considerare, ƿ este densitatea fluidului, P este presiunea fluidului, g este valoarea accelerației gravitației și z este înălțimea măsurată în direcția gravitației.

În ecuația lui Bernoulli este implicit faptul că energia unui fluid constă din trei componente:

- O componentă cinetică, care este cea care rezultă din viteza cu care se mișcă fluidul.

- O componentă potențială sau gravitațională, care se datorează înălțimii la care se află fluidul.

- O energie de presiune, care este aceea pe care o posedă fluidul ca o consecință a presiunii la care este supus.

Pe de altă parte, ecuația lui Bernoulli poate fi exprimată și astfel:

v₁ ^Două ∙ ƿ / 2 + P₁ + ƿ ∙ g ∙ z₁ = v_Două^Două ∙ ƿ / 2 + P_Două + ƿ ∙ g ∙ z_Două

Această ultimă expresie este foarte practică pentru a analiza schimbările pe care le experimentează un fluid atunci când oricare dintre elementele care alcătuiesc ecuația se schimbă.

Formă simplificată

În anumite ocazii, modificarea termenului ρgz al ecuației lui Bernoulli este minimă comparativ cu cea experimentată de ceilalți termeni, deci poate fi neglijată. De exemplu, acest lucru se întâmplă în curenții experimentați de un avion în zbor..

Cu aceste ocazii, ecuația lui Bernoulli este exprimată după cum urmează:

P + q = P₀

În această expresie q este presiune dinamică și este echivalentă cu v ^Două ∙ ƿ / 2 și P₀ este ceea ce se numește presiune totală și este suma presiunii statice P și a presiunii dinamice q.

Aplicații

Teorema lui Bernoulli are multe și diverse aplicații în domenii la fel de diverse precum știința, ingineria, sportul etc..

O aplicație interesantă se găsește în proiectarea șemineelor. Coșurile de fum sunt construite înalte pentru a obține o diferență mai mare de presiune între bază și ieșirea coșului de fum, datorită căreia este mai ușor de extras gazele de ardere.

Desigur, ecuația lui Bernoulli se aplică și studiului mișcării fluxurilor de lichid în conducte. Din ecuație rezultă că o reducere a secțiunii transversale a țevii, pentru a crește viteza fluidului care trece prin ea, implică, de asemenea, o scădere a presiunii.

Ecuația Bernoulli este utilizată și în aviație și în vehiculele de Formula 1. În cazul aviației, efectul Bernoulli este originea ascensiunii avioanelor..

Aripile aeronavelor sunt proiectate cu scopul de a obține un flux de aer mai mare în partea superioară a aripii.

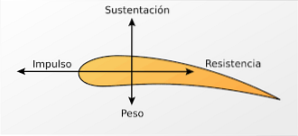
Astfel, în partea superioară a aripii viteza aerului este mare și, prin urmare, presiunea este mai mică. Această diferență de presiune produce o forță direcționată vertical în sus (forța de ridicare) care permite aeronavei să plutească în aer. Un efect similar se obține la eleronele mașinilor de Formula 1.

Exercițiul a fost rezolvat

Printr-o conductă cu secțiune transversală de 4,2 cm^Două un curent de apă curge la 5,18 m / s. Apa coboară de la o înălțime de 9,66 m la un nivel inferior cu o înălțime zero, în timp ce aria secțiunii transversale a tubului crește la 7,6 cm^Două.

a) Calculați viteza curentului de apă la nivelul inferior.

b) Determinați presiunea la nivelul inferior știind că presiunea la nivelul superior este de 152000 Pa.

Soluţie

a) Având în vedere că fluxul trebuie conservat, este adevărat că:

Î_{Nivelul superior} = Î_{nivel inferior}

 v₁ . S₁ = v_Două . S_Două

 5,18 m / s. 4,2 cm^Două = v_Două . 7,6 cm ^^Două

Rezolvând pentru, se obține că:

v_Două = 2,86 m / s

b) Aplicarea teoremei lui Bernoulli între cele două niveluri și luând în considerare faptul că densitatea apei este de 1000 kg / m³ , se obține că:

v₁ ^Două ∙ ƿ / 2 + P₁ + ƿ ∙ g ∙ z₁ = v_Două^Două ∙ ƿ / 2 + P_Două + ƿ ∙ g ∙ z_Două

(1/2). 1000 kg / m³ . (5,18 m / s)^Două + 152000 + 1000 kg / m³ . 10 m / s^Două . 9,66 m =

= (1/2). 1000 kg / m³ . (2,86 m / s)^Două + P_Două + 1000 kg / m³ . 10 m / s^Două . 0 m

Rezolvarea pentru P_Două ajungi la:

P_Două = 257926,4 Pa

Referințe

1. Principiul lui Bernoulli. (n.d.). Pe Wikipedia. Adus pe 12 mai 2018, de pe es.wikipedia.org.
2. Principiul lui Bernoulli. (n.d.). În Wikipedia. Adus pe 12 mai 2018, de pe en.wikipedia.org.
3. Batchelor, G.K. (1967). O introducere în dinamica fluidelor. Cambridge University Press.
4. Lamb, H. (1993). Hidrodinamică (Ed. A 6-a). Cambridge University Press.
5. Mott, Robert (1996). Mecanica fluidelor aplicată (Ed. A 4-a). Mexic: Pearson Education.