Descrierea teoremei Norton, aplicații, exemple și exerciții

Teorema lui Norton, care se aplică circuitelor electrice, stabilește că un circuit liniar cu două terminale a și b, poate fi înlocuit cu unul complet echivalent, care constă dintr-o sursă de curent numită I_Nu conectat în paralel cu un rezistor R_Nu.

A spus curentul I_Nu Am auzit_N Este cel care ar curge între punctele a și b, dacă ar fi scurtcircuitate. Rezistența R_N este rezistența echivalentă între terminale, atunci când toate sursele independente se opresc. Tot ce se spune este prezentat în figura 1.

Caseta neagră din figură conține circuitul liniar care trebuie înlocuit cu echivalentul său Norton. Un circuit liniar este unul în care intrarea și ieșirea au o dependență liniară, cum ar fi relația dintre tensiunea V și curentul continuu I într-un element ohmic: V = I.R.

Această expresie corespunde legii lui Ohm, unde R este rezistența, care poate fi și o impedanță, dacă este un circuit de curent alternativ.

Teorema lui Norton a fost dezvoltată de inginerul electric și inventatorul Edward L. Norton (1898-1983), care a lucrat mult timp pentru Bell Labs..

Indice articol

• 1 Aplicații ale teoremei lui Norton
  • 1.1 Relația dintre teoremele Norton și Thevenin
• 2 Exemplu
• 3 Exercițiul a fost rezolvat
• 4 Referințe

Aplicații ale teoremei lui Norton

Când aveți rețele foarte complicate, cu multe rezistențe sau impedanțe și doriți să calculați tensiunea dintre oricare dintre ele sau curentul care curge prin ea, teorema lui Norton simplifică calculele, deoarece așa cum am văzut, rețeaua poate fi înlocuită cu un circuit mai mic și mai ușor de gestionat.

În acest fel, teorema lui Norton este foarte importantă la proiectarea circuitelor cu elemente multiple, precum și la studierea răspunsului acestora..

Relația dintre teoremele lui Norton și Thevenin

Teorema lui Norton este dualitatea teoremei lui Thevenin, ceea ce înseamnă că sunt echivalente. Teorema lui Thevenin indică faptul că cutia neagră din figura 1 poate fi înlocuită cu o sursă de tensiune în serie cu un rezistor, numit rezistența Thevenin R_Th. Acest lucru este exprimat în următoarea figură:

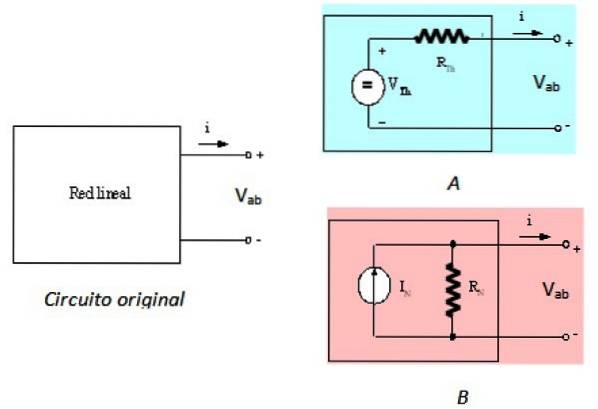
Circuitul din stânga este circuitul original, rețeaua liniară din cutia neagră, circuitul A din dreapta sus este echivalentul Thevenin și circuitul B este echivalentul Norton, așa cum este descris. Privite de la bornele a și b, cele trei circuite sunt echivalente.

Acum rețineți că:

-În circuitul original, tensiunea dintre terminale este V_ab.

-V_ab  = V_Th în circuit LA

-În cele din urmă, V_ab  = Eu_N.R_N în circuit B

Dacă bornele a și b sunt scurtcircuitate în toate cele trei circuite, trebuie să ne asigurăm că tensiunea și curentul dintre aceste puncte trebuie să fie aceleași pentru toate cele trei, deoarece acestea sunt echivalente. Atunci:

-În circuitul original curentul este i.

-Pentru circuitul A, curentul este i = V_Th / R_Th, conform legii lui Ohm.

-În cele din urmă în circuitul B, curentul este I_N

Prin urmare, se concluzionează că rezistențele Norton și Thevenin au aceeași valoare și că curentul este dat de:

i = eu_N = V_Th / R_Th = V_Th / R_N

Exemplu

Pentru a aplica corect teorema Norton, sunt urmați următorii pași:

-Izolați din rețea secțiunea circuitului pentru care se găsește echivalentul Norton.

-În circuitul rămas, indicați bornele a și b.

-Înlocuiți sursele de tensiune pentru scurtcircuite și sursele de curent pentru circuitele deschise, pentru a găsi rezistența echivalentă între bornele a și b. Acesta este R_N.

-Întoarceți toate sursele la pozițiile lor inițiale, bornele de scurtcircuit a și b și găsiți curentul care curge între ele. Acesta sunt eu_N.

-Desenați circuitul echivalent Norton în conformitate cu ceea ce este indicat în figura 1. Atât sursa de curent, cât și rezistența echivalentă sunt în paralel.

De asemenea, puteți aplica teorema lui Thevenin pentru a găsi R_Th, că știm deja că este egal cu R_N, apoi prin legea lui Ohm îl poți găsi pe I_N și continuați să trageți circuitul rezultat.

Și acum să vedem un exemplu:

Găsiți echivalentul Norton dintre punctele A și B ale următorului circuit:

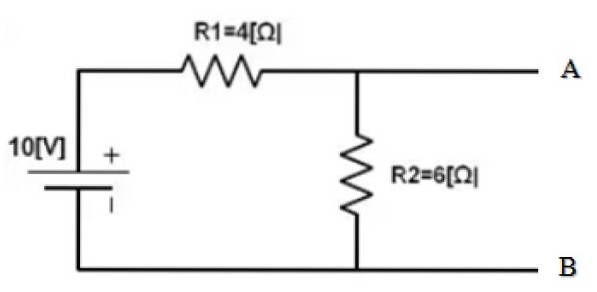
Partea circuitului al cărei echivalent trebuie găsit este deja izolată. Iar punctele A și B sunt clar determinate. Următorul este scurtcircuitarea sursei de 10 V și găsirea rezistenței echivalente a circuitului obținut:

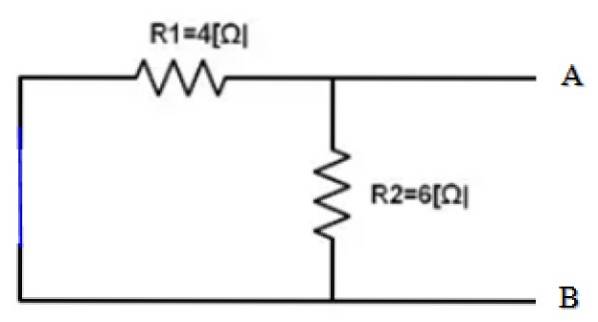
Vizualizări de la terminalele A și B, ambele rezistențe R₁ și R_Două sunt în paralel, prin urmare:

1 / R_echiv = 1 / R₁₂ = (1/4) + (1/6) Ω^-1 = 5/12 Ω^-1  → R_echiv = 12/5 Ω = 2,4 Ω

Apoi sursa este readusă la locul său și punctele A și B sunt scurtcircuitate pentru a găsi curentul care circulă acolo, acesta va fi I_N. În acest caz:

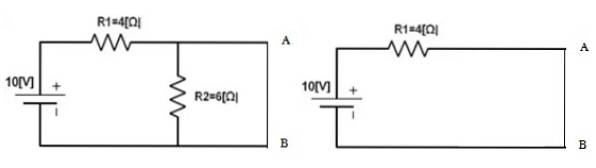
Eu_N = 10 V / 4 Ω = 2,5 A

Echivalent Norton

În cele din urmă, echivalentul Norton este desenat cu valorile găsite:

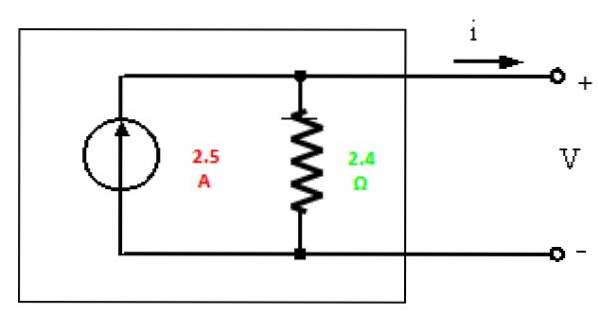
Exercițiul a fost rezolvat

În circuitul din următoarea figură:

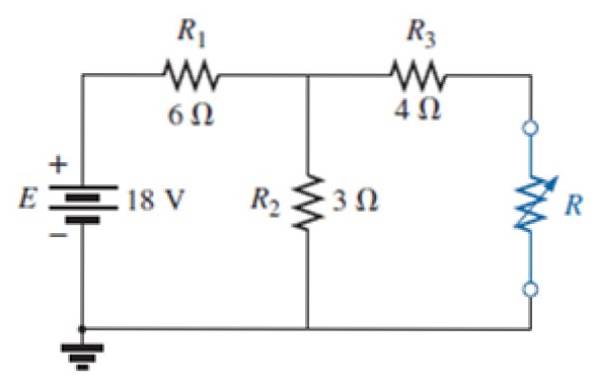
a) Găsiți circuitul echivalent Norton al rețelei externe la rezistorul albastru.

b) Găsiți și echivalentul Thévenin.

Solutie la

Urmând pașii indicați mai sus, sursa trebuie scurtcircuitată:

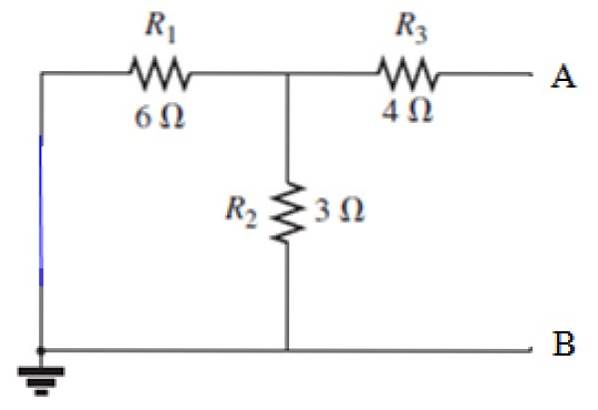
Calculul RN

Vedere de la bornele A și B, rezistorul R₃ este în serie cu paralela formată din rezistențele R₁ și R_Două, să calculăm mai întâi rezistența echivalentă a acestei paralele:

1 / R₁₂ = (1/6) + (1/3) Ω^-1 = 1/2 Ω^-1  → R_echiv = 2/1 Ω = 2Ω

Și atunci această paralelă este în serie cu R_3, astfel încât rezistența echivalentă este:

R_echiv = 2 Ω + 4 Ω = 6 Ω

Aceasta este valoarea ambelor R_N ca din R_Th, după cum s-a explicat mai înainte.

În calcul

Terminalele A și B sunt apoi scurtcircuitate, readucând sursa la locul său:

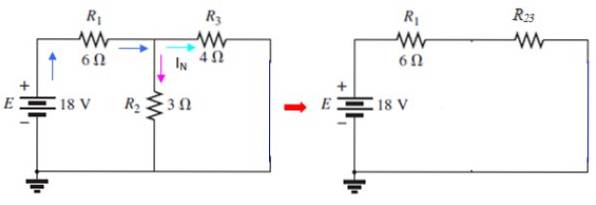
Curentul prin I₃ este actualul I_N căutat, care poate fi determinat folosind metoda mesh sau folosind serie și paralel. În acest circuit R_Două și R₃ sunt în paralel:

1 / R_{2. 3} = (1/3) + (1/4) Ω^-1 = 7/12 Ω^-1  → R_{2. 3} = 12/7 Ω

Rezistența R₁ este în serie cu această paralelă, atunci:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Curentul care părăsește sursa (culoarea albastră) este calculat folosind legea lui Ohm:

V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 A

Acest curent este împărțit în două părți: una care trece prin R_Două și altul care traversează R₃. Cu toate acestea, curentul prin paralela R_{2. 3} este același lucru care trece prin R₁, așa cum se vede în circuitul intermediar din figură. Tensiunea este:

V_{2. 3} = I.R_{2. 3} = (7/3) A. (12/7) Ω = 4 V

Ambele rezistențe R_Două și R₃ sunt la acea tensiune, deoarece sunt în paralel, prin urmare:

Eu₃ = V_{2. 3} / R₃ = 4 V / 4 Ω = 1 A

Avem deja căutat curentul Norton, deoarece așa cum am spus anterior am₃ = Eu_N, atunci:

Eu_N = 1 A

Echivalent Norton

Totul este pregătit pentru a atrage echivalentul Norton al acestui circuit între punctele A și B:

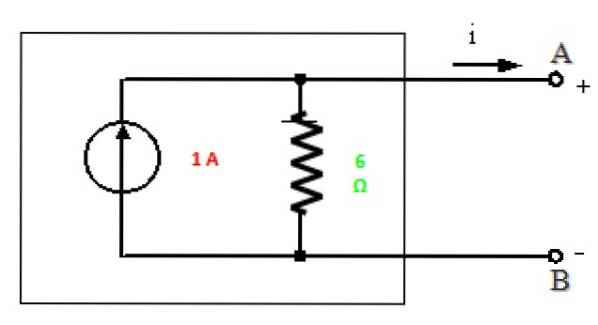
Soluția b

Găsirea echivalentului Thévenin este foarte simplă, deoarece R_Th = R_N= 6 Ω și așa cum este explicat în secțiunile precedente:

V_Th = Eu_N. R_N = 1 A. 6 Ω = 6 V

Circuitul echivalent Thévenin este:

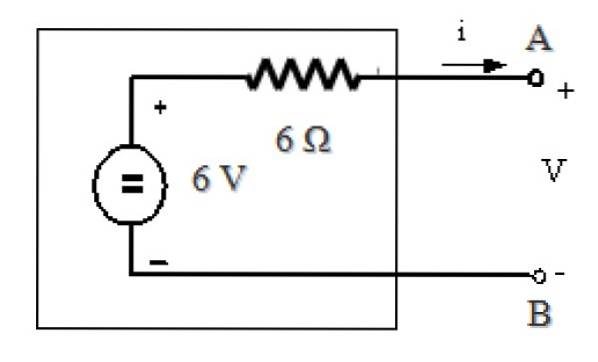
Referințe

1. Alexander, C. 2006. Bazele circuitelor electrice. A treia. Ediție. Mc Graw Hill.
2. Boylestad, R. 2011. Introducere în analiza circuitelor. Al 2-lea. Ediție. Pearson.
3. Dorf, R. 2006. Introducere în circuite electrice. Al 7-lea. Ediție. John Wiley & Sons.
4. Edminister, J. 1996. Circuite electrice. Seria Schaum. A treia. Ediție. Mc Graw Hill.
5. Wikipedia. Teorema lui Norton. Recuperat de pe: es.wikipedia.org.