Teorema fundamentală a dovezii aritmetice, aplicații, exerciții

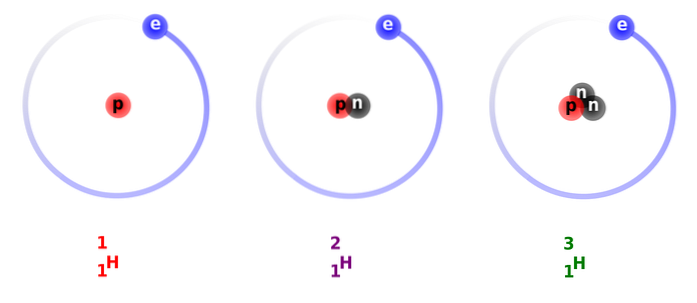
Teorema fundamentală a aritmeticii afirmă că orice număr natural mai mare de 1 poate fi descompus ca produs al numerelor prime - unele pot fi repetate - și această formă este unică pentru acel număr, deși ordinea factorilor poate fi diferită.

Reamintim că un număr prim p Este cel care se admite doar pe sine și 1 ca divizori pozitivi. Următoarele numere sunt prime: 2, 3, 5, 7, 11, 13 și așa mai departe, deoarece există infinități. Numărul 1 nu este considerat prim, deoarece are un singur divizor.

La rândul lor, se apelează numerele care nu respectă cele de mai sus numere compuse, ca 4, 6, 8, 9, 10, 12, 14 ... Să luăm de exemplu numărul 10 și imediat vedem că poate fi descompus ca produs de 2 și 5:

10 = 2 × 5

Atât 2, cât și 5 sunt, efectiv, numere prime. Teorema afirmă că acest lucru este posibil pentru orice număr n:

Unde p₁, p_Două, p₃... p_r sunt numere prime și k₁, k_Două, k₃,... k_r sunt numere naturale. Deci numerele prime acționează ca niște cărămizi din care, prin multiplicare, se construiesc numerele naturale.

Indice articol

• 1 Dovada teoremei fundamentale a aritmeticii
  • 1.1 Unicitatea factorizării prime
• 2 Aplicații
  • 2.1 Numere prime în natură
  • 2.2 Numere prime și cumpărături online
• 3 exerciții rezolvate
  • 3.1 - Exercițiul 1
  • 3.2 - Exercițiul 2
• 4 Referințe

Dovada teoremei fundamentale a aritmeticii

Începem prin a arăta că fiecare număr poate fi descompus în factori primi. Fie un număr natural n> 1, prim sau compus.

De exemplu, dacă n = 2, acesta poate fi exprimat ca: 2 = 1 × 2, care este prim. În același mod, continuați cu următoarele numere:

3 = 1 × 3

4 = 2 × 2

5 = 1 × 5

6 = 2 × 3

7 = 1 × 7

8 = 2 × 2 × 2

Continuăm așa, descompunând toate numerele naturale până ajungem la numărul n -1. Să vedem dacă o putem face cu următorul număr: n.

Dacă n este prim, îl putem descompune ca n = 1 × n, dar să presupunem că n este compus și are un divizor d, logic mai mic decât n:

1< d < n.

Dacă n / d = p₁, cu P₁ un număr prim, atunci n se scrie ca:

n = p₁.d

Dacă d este prim, nu mai este nimic de făcut, dar dacă nu este, există un număr n_Două care este divizor al lui d și mai mic decât acesta: n_Două < d, por lo que d podrá escribirse como el producto de n_Două cu un alt număr prim p_Două:

d = p_Două n_Două

Că atunci când înlocuiți numărul original n ar da:

n = p₁ .p_Două .n_Două

Acum să presupunem că n_Două fie este un număr prim și îl scriem ca produs al unui număr prim p₃, de către un divizor al tău n₃, astfel încât n₃ < n_Două < n₁ < n:

n_Două = p₃.n₃ → n = p₁ p_Două p₃.n₃

 Repetăm ​​această procedură de un număr finit de ori până obținem:

n = p₁.p_Două.p₃ ... p_r

Aceasta înseamnă că este posibil să se descompună toata lumea numere întregi de la 2 la n, ca produs al numerelor prime.

Unicitatea factorizării prime

Acum să verificăm că, cu excepția ordinii factorilor, această descompunere este unică. Să presupunem că n poate fi scris în două moduri:

n = p₁.p_Două.p₃ ... p_r = q_1.ce_Două.ce₃... ce_s  (cu r ≤ s)

Desigur că₁, ce_Două, ce₃... sunt și numere prime. Precum p₁ împarte un (q_1.ce_Două.ce₃... ce_s) Apoi p₁ este egal cu oricare dintre „q”, nu contează la care, deci putem spune că p₁ = q₁. Împărțim n cu p₁ și obținem:

p_Două.p₃ ... p_r =_.ce_Două.ce₃... ce_s

Repetăm ​​procedura până când împărțim totul la p_r, atunci primim:

1 = q_{r + 1}... ce_s

Dar nu se poate ajunge la ce_{r + 1}... ce_s = 1 când r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.

Aplicații

După cum am mai spus, numerele prime reprezintă, dacă vreți, atomii numerelor, componentele lor de bază. Deci, teorema fundamentală a aritmeticii are numeroase aplicații, cea mai evidentă: putem lucra mai ușor cu numere mari dacă le exprimăm ca produs al numerelor mai mici..

În același mod, putem găsi cel mai mare multiplu comun (MCM) și cel mai mare divizor comun (MCD), o procedură care ne ajută să facem sume de fracții mai ușor, să găsim rădăcini de numere mari sau să operăm cu radicali, rezolva probleme de aplicare de o natură foarte diversă.

Mai mult, numerele prime sunt extrem de enigmatice. Un model nu este încă recunoscut în ele și nu este posibil să știm care va fi următorul. Cel mai mare de până acum a fost găsit de computere și are 24.862.048 cifre, deși noile numere prime apar mai rar de fiecare dată.

Numere prime în natură

Cicalele, cicadele sau cicadele care trăiesc în nord-estul Statelor Unite apar în cicluri de 13 sau 17 ani. Amândoi sunt numere prime.

În acest fel, cicadele evită să coincidă cu prădătorii sau concurenții care au alte perioade de naștere și nici diferitele soiuri de cicade nu concurează între ele, deoarece nu coincid în același an..

Numere prime și cumpărături online

Numerele prime sunt utilizate în criptografie pentru a păstra secretele detaliilor cardului de credit atunci când se efectuează achiziții pe internet. În acest fel, datele despre care cumpărătorul ajunge exact la magazin fără a se pierde sau a cădea în mâinile unor oameni fără scrupule..

Cum? Datele de pe carduri sunt codificate într-un număr N care poate fi exprimat ca produs al numerelor prime. Aceste numere prime sunt cheia pe care o dezvăluie datele, dar sunt necunoscute publicului, pot fi decodate numai pe web către care sunt direcționate.

Descompunerea unui număr în factori este o sarcină ușoară dacă numerele sunt mici (vezi exercițiile rezolvate), dar în acest caz se folosesc ca cheie numere prime de 100 de cifre, care la multiplicarea lor dau numere mult mai mari, a căror descompunere detaliată implică o sarcină uriașă.

Exerciții rezolvate

- Exercitiul 1

Descompuneți 1029 în factori primi.

Soluţie

1029 este divizibil cu 3. Se știe deoarece atunci când se adaugă cifrele sale suma este multiplu de 3: 1 + 0 + 2 + 9 = 12. Deoarece ordinea factorilor nu modifică produsul, putem începe de aici:

1029 3

343

1029 = 3 × 343

Pe de altă parte 343 = 7³, atunci:

1029 = 3 × 7³ = 3 × 7 × 7 × 7

Și întrucât atât 3, cât și 7 sunt numere prime, aceasta este descompunerea lui 1029.

- Exercițiul 2

Factorizați x-ul trinomial^Două + 42x + 432.

Soluţie

Trinomul este rescris sub forma (x + a). (x + b) și trebuie să găsim valorile lui a și b, astfel încât:

a + b = 42; a.b = 432

Numărul 432 este descompus în factori primi și de acolo combinația adecvată este aleasă prin încercare și eroare, astfel încât factorii adăugați să dea 42.

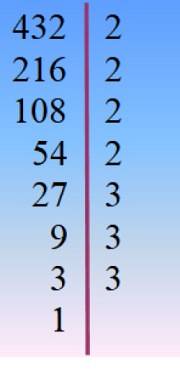
432 = 2⁴ × 3³ = 2 × 3³× 2³ = 2⁴× 3^Două × 3 = ...

De aici există mai multe posibilități de a scrie 432:

432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72 ... .

Și toate pot fi găsite prin combinarea produselor între factorii primi, dar pentru a rezolva exercițiul propus, singura combinație adecvată este: 432 = 24 × 18 din 24 + 18 = 42, apoi:

X^Două + 42x + 432 = (x + 24). (x +18)

Referințe

1. Baldor, A. 1986. Aritmetica practică teoretică. Compañía Cultural Editora de Textos Americanos S.A.
2. BBC World. Codul ascuns al naturii. Recuperat de pe: bbc.com.
3. De Leon, Manuel Numere prime: gardienii internetului. Recuperat de pe: blogs.20minutos.es.
4. UNAM. Teoria numerelor I: Teorema fundamentală a aritmeticii. Recuperat de pe: teoriadenumeros.wikidot.com.
5. Wikipedia. Teorema fundamentală a aritmeticii. Recuperat de pe: es.wikipedia.org.