A treia lege a lui Newton, numit si legea acțiunii și reacției afirmă că atunci când un obiect exercită forță asupra altui, acesta din urmă exercită și asupra primului o forță de mărime și direcție egală și direcție opusă.
Isaac Newton și-a făcut cunoscute cele trei legi în 1686 în cartea sa Philosophiae Naturalis Principia Mathematica o Principiile matematice ale filosofiei naturale.
Indice articol
Formularea matematică a celei de-a treia legi a lui Newton este foarte simplă:
F12 = -Fdouăzeci și unu
Una dintre forțe se numește acțiune iar cealaltă este reacţie. Cu toate acestea, este necesar să subliniem importanța acestui detaliu: ambele acționează asupra unor obiecte diferite. De asemenea, o fac simultan, deși această terminologie sugerează incorect că acțiunea are loc înainte și reacția după..
Deoarece forțele sunt vectori, acestea sunt notate cu caractere aldine. Această ecuație indică faptul că avem două obiecte: obiectul 1 și obiectul 2. Forța F12 este cea exercitată de obiectul 1 asupra obiectului 2. Forța Fdouăzeci și unu este exercitat de obiectul 2 asupra obiectului 1. Și semnul (-) indică faptul că sunt opuse.
Când se observă cu atenție a treia lege a lui Newton, se observă o diferență importantă cu primele două: în timp ce invocă un singur obiect, a treia lege se referă la două obiecte diferite.
Și este că, dacă vă gândiți cu atenție, interacțiunile necesită perechi de obiecte.
Din acest motiv, forțele de acțiune și reacție nu se anulează reciproc sau se echilibrează, deși au aceeași magnitudine și direcție, ci direcția opusă: sunt aplicate diferitelor corpuri..
Iată o aplicație foarte cotidiană a unei interacțiuni legate de a treia lege a lui Newton: o minge care cade vertical și Pământul. Mingea cade la pământ, deoarece Pământul exercită o forță de atracție, cunoscută sub numele de gravitație. Această forță determină căderea mingii cu o accelerație constantă de 9,8 m / sDouă.
Cu toate acestea, aproape nimeni nu se gândește la faptul că mingea exercită și o forță atractivă pe Pământ. Desigur, pământul rămâne neschimbat, deoarece masa sa este mult mai mare decât cea a mingii și, prin urmare, are o accelerare neglijabilă.
Un alt punct notabil despre a treia lege a lui Newton este că nu este necesar contactul dintre cele două obiecte care interacționează. Este evident din exemplul citat recent: mingea nu a luat încă contact cu Pământul, dar își exercită totuși atracția. Și mingea și pe Pământ.
O forță precum gravitația, care acționează indistinct dacă există sau nu contact între obiecte, se numește „forță de acțiune la distanță”. Pe de altă parte, forțe precum fricțiunea și normalul, necesită ca obiectele care interacționează să fie în contact, de aceea sunt numite „forțe de contact”.
Revenind la perechea de obiecte mingea - Pământ, alegând indicii P pentru minge și T pentru pământ și aplicând a doua lege a lui Newton fiecărui participant la acest sistem, obținem:
Frezultând = m.la
A treia lege prevede că:
mPlaP = - mTlaT
laP = 9,8 m / sDouă îndreptate vertical în jos. Deoarece această mișcare are loc de-a lungul direcției verticale, se poate renunța la notația vectorială (aldină); și alegând direcția ascendentă la fel de pozitivă și descendentă ca negativă, avem:
laP = 9,8 m / sDouă
mT ≈ 6 x 10 24 Kg
Indiferent de masa mingii, accelerația Pământului este zero. De aceea se observă că mingea cade spre Pământ și nu invers..
Rachetele sunt un bun exemplu de aplicare a celei de-a treia legi a lui Newton. Racheta prezentată în imagine la început crește datorită propulsiei gazelor fierbinți la viteză mare.
Mulți cred că acest lucru se întâmplă deoarece aceste gaze cumva se „sprijină” pe atmosferă sau pe sol pentru a susține și a propulsa racheta. Nu funcționează așa.
La fel cum racheta exercită forță asupra gazelor și le expulză înapoi, gazele exercită o forță asupra rachetei, care are același modul, dar direcție opusă. Această forță este cea care dă rachetei accelerarea ascendentă.
Dacă nu aveți o astfel de rachetă la îndemână, există alte modalități de a verifica dacă a treia lege a lui Newton funcționează pentru a oferi propulsie. Pot fi construite rachete de apă, în care împingerea necesară este asigurată de apa expulzată cu ajutorul unui gaz sub presiune..
Trebuie remarcat faptul că pornirea unei rachete de apă necesită timp și necesită multe precauții.
O modalitate mai accesibilă și mai imediată de a verifica efectul celei de-a treia legi a lui Newton este prin îmbrăcarea unei perechi de patine și propulsarea de un perete..
De cele mai multe ori, capacitatea de a exercita forța este asociată cu obiectele care se află în mișcare, dar adevărul este că și obiectele imobile pot exercita forțe. Patinatorul este împins înapoi datorită forței pe care peretele imobil îl exercită asupra lui.
Suprafețele în contact exercită forțe de contact (normale) între ele. Când o carte se sprijină pe o masă orizontală, exercită asupra ei o forță verticală numită normală. Cartea exercită pe masă o forță verticală de aceeași valoare numerică și direcție opusă.
Copiii și adulții pot experimenta cu ușurință a treia lege a lui Newton și pot verifica dacă forțele de acțiune și reacție nu se anulează reciproc și sunt capabile să asigure mișcări..
Doi patinatori pe gheață sau pe o suprafață foarte netedă se pot propulsa reciproc și pot experimenta mișcări în direcția opusă, indiferent dacă au sau nu aceeași masă, datorită legii acțiunii și reacției.
Luați în considerare doi patinatori cu mase destul de diferite. Se află în mijlocul unui patinoar cu frecare neglijabilă și sunt inițial în repaus. La un moment dat se împing reciproc aplicând forță constantă cu palmele mâinilor. Cum se vor mișca amândoi?
Este important de reținut că, din moment ce este o suprafață fără frecare, singurele forțe dezechilibrate sunt forțele pe care patinatorii le aplică reciproc. Deși greutatea și acțiunea normală asupra ambelor, aceste forțe se echilibrează, altfel patinatorii ar accelera în direcție verticală.
A treia lege a lui Newton prevede că:
F12 = -Fdouăzeci și unu
Adică, forța exercitată de patinatorul 1 la 2 este egală în mărime cu cea exercitată de 2 la 1, cu aceeași direcție și direcție opusă. Rețineți că aceste forțe sunt aplicate diferitelor obiecte, în același mod în care forțele au fost aplicate mingii și Pământului în exemplul conceptual anterior..
m1 la1 = -mDouă laDouă
Deoarece forțele sunt opuse, accelerațiile pe care le provoacă vor fi, de asemenea, opuse, dar magnitudinile lor vor fi diferite, deoarece fiecare patinator are o masă diferită. Să ne uităm la accelerația dobândită de primul patinator:
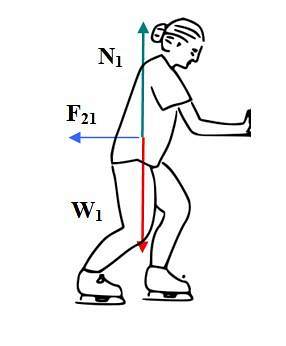
Deci, mișcarea care se întâmplă în continuare este separarea ambilor patinatori în direcții opuse. În principiu, patinatorii erau odihniți în mijlocul pistei. Fiecare exercită o forță asupra celeilalte care oferă accelerație atâta timp cât mâinile sunt în contact și împingerea durează.
După aceea, patinatorii se îndepărtează unul de celălalt cu o mișcare rectilinie uniformă, deoarece forțele dezechilibrate nu mai acționează. Viteza fiecărui patinator va fi diferită dacă și masele lor sunt.
Pentru a rezolva problemele în care legile lui Newton trebuie aplicate, este necesar să atragem cu atenție forțele care acționează asupra obiectului. Acest desen se numește „diagramă cu corp liber” sau „diagramă cu corp izolat”. Forțele exercitate de corp asupra altor obiecte nu trebuie prezentate în această diagramă..
Dacă există mai multe obiecte implicate în problemă, este necesar să desenați o diagramă a corpului liber pentru fiecare dintre obiecte, amintind că perechile acțiune-reacție acționează asupra unor corpuri diferite..
1- Patinatorii secțiunii anterioare au mase respective m1 = 50 kg și mDouă = 80 kg. Se împing reciproc cu o forță constantă de 200 N. Împingerea durează 0,40 secunde. Găsi:
a) Accelerația pe care o dobândește fiecare patinator datorită forței.
b) Viteza fiecărei intrări atunci când se separă
a) Luați ca direcție orizontală pozitivă cea care merge de la stânga la dreapta. Aplicând a doua lege a lui Newton cu valorile oferite de enunț, avem:
Fdouăzeci și unu = m1la1
De unde:
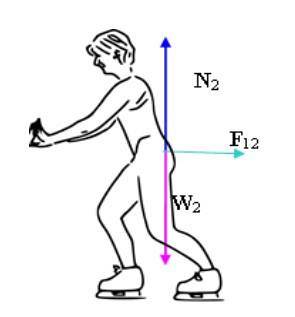
Pentru al doilea patinator:
b) Pentru a calcula viteza pe care o poartă tocmai la separare, se folosesc ecuațiile cinematice ale mișcării rectilinii uniform accelerate:
Viteza inițială este 0, deoarece erau în repaus în mijlocul pistei:
vF = la
vf1 = a1t = -4 m / sDouă . 0,40 s = -1,6 m / s
vf2 = aDouăt = +2,5 m / sDouă . 0,40 s = +1 m / s
După cum era de așteptat, persoana 1, fiind mai ușoară, capătă o accelerație mai mare și, prin urmare, o viteză mai mare. Acum rețineți următoarele despre produsul masei și viteza fiecărui patinator:
m1 v1 = 50 kg. (-1,6 m / s) = - 80 kg.m / s
mDouă vDouă = 80 kg. 1 m / s = +80 kg.m / s
Suma ambelor produse este 0. Produsul masei și al vitezei se numește impuls P. Este un vector cu aceeași direcție și sens de viteză. Când patinatorii erau în repaus și mâinile lor erau în contact, se putea presupune că au format același obiect al cărui impuls era:
Psau = (m1 +mDouă) vsau = 0
După sfârșitul apăsării, cantitatea de mișcare a sistemului de patinaj rămâne 0. Prin urmare, cantitatea de mișcare este conservată.
Mersul pe jos este una dintre cele mai cotidiene acțiuni care pot fi efectuate. Dacă este observată cu atenție, acțiunea mersului necesită împingerea piciorului împotriva solului, astfel încât să redea o forță egală și opusă pe piciorul de mers..
Tocmai acea forță permite oamenilor să meargă. În zbor, păsările exercită forță asupra aerului și aerul împinge aripile, astfel încât pasărea să se propulseze înainte.
Într-o mașină, roțile exercită forțe asupra trotuarului. Datorită reacției pavajului, exercită forțe asupra anvelopelor care propulsează mașina înainte.
În sport, forțele de acțiune și reacție sunt numeroase și au o participare foarte activă.
De exemplu, să-l vedem pe sportiv cu piciorul sprijinit pe un bloc de start. Blocul oferă o forță normală ca reacție la apăsarea pe care o exercită sportivul asupra sa. Rezultatul acestui normal și greutatea alergătorului au ca rezultat o forță orizontală care permite sportivului să se propulseze înainte..
Un alt exemplu în care este prezentă a treia lege a lui Newton este la pompierii care dețin furtunuri de incendiu. Capătul acestor furtunuri mari are un mâner pe duza pe care pompierul trebuie să o țină la ieșirea jetului de apă, pentru a evita reculul care apare atunci când apa se grăbește.
Din același motiv, este convenabil să legați bărcile de doc înainte de a le părăsi, deoarece atunci când se împing pentru a ajunge la doc, se oferă o forță bărcii care o îndepărtează de acesta..
Nimeni nu a comentat acest articol încă.