Concept de variație liniară, exemple, exercițiu rezolvat

variație liniară apare între două mărimi fizice atunci când graficul care le reprezintă este o linie dreaptă. Este echivalent cu afirmarea că variabilele sunt în dependență liniară, în așa fel încât, dacă numim una dintre ele „y” și cealaltă „x”, ele vor fi corelate prin intermediul expresiei matematice:

y = mx + b

În această formulă, m și b sunt numere reale. Valoarea lui m reprezintă panta sau înclinarea liniei - care este întotdeauna constantă - și b este tăierea liniei cu axa verticală.

Fiecare fenomen care răspunde la o variație liniară are nume diferite pentru variabile, așa cum vom vedea în următoarele exemple. Cu toate acestea, forma matematică a ecuației este aceeași.

Experimental se poate stabili dacă există o relație liniară între două mărimi, măsurând perechile de valori (x, y).

Punctele astfel obținute sunt reprezentate grafic pe hârtie milimetrică și se observă dacă au o tendință liniară, adică dacă există o linie care se potrivește în mod adecvat cu datele experimentale.

În prima instanță, această linie poate fi trasată vizual, dar prin intermediul unui regresie liniara pot fi găsite analitic, valorile m și b ale liniei care se potrivesc cel mai bine punctelor experimentale.

Indice articol

• 1 Exemple de variație liniară
  • 1.1 Viteza în mișcare rectilinie variază uniform
  • 1.2 Expansiunea termică
  • 1.3 Poziția unui mobil cu viteză constantă
  • 1.4 Înălțimea unei persoane
  • 1.5 Scale de temperatură
  • 1.6 Presiune și adâncime
• 2 Exercițiul a fost rezolvat
  • 2.1 Costul conducerii
• 3 Referințe

Exemple de variație liniară

Există numeroase fenomene naturale, precum și relații stabilite între standardele de măsurare, care se datorează variației liniare, de exemplu:

Viteza în mișcare rectilinie a variat uniform

Viteza în funcție de timpul v (t) al unui mobil care se deplasează de-a lungul unei linii cu accelerație constantă a și viteza inițială v_sau  diferită de 0. Această mișcare este cunoscută sub numele de mișcare rectilinie uniform variată iar ecuația pentru viteză este:

v (t) = v_sau + la

Expansiunea termică

Un alt fenomen natural a cărui variație este liniară este creșterea în lungime pe care o tijă sau sârmă o experimentează atunci când este încălzită..

Într-adevăr, atunci când temperatura oricărui obiect crește, crește și dimensiunile sale, iar această creștere depinde de schimbarea temperaturii ΔT și de o cantitate numită coeficient de expansiune liniară notată cu litera greacă α:

L = L_sau + α ΔT

În această expresie L este lungimea finală a obiectului și L_sau este lungimea sa inițială.

Poziția unui mobil cu viteză constantă

Un mobil cu viteză constanta se mișcă întotdeauna în linie dreaptă. Dacă linia dreaptă este axa orizontală x, poziția x (t) în orice moment este dată de:

x (t) = x_sau + vt

Unde x_sau este poziția inițială, v este viteza și t este timpul. În acest fel se spune că poziția x variază liniar cu timpul t.

Înălțimea unei persoane

Medicii și antropologii pot estima înălțimea unei persoane măsurând lungimea femurului..

Cu cât o persoană este mai înaltă, cu atât sunt mai lungi picioarele, deci există modele liniare pentru a prezice înălțimea unui adult H (în inci) dacă lungimea L (de asemenea, în inci) a femurului său este cunoscută, conform ecuației:

H = 1,880⋅L + 32,010

Scale de temperatură

Cântarele Celsius și Fahrenheit sunt utilizate zilnic pentru a măsura temperaturile. Această ultimă scară este frecvent utilizată în țările vorbitoare de limbă engleză. Există o echivalență pentru a merge de la unul la altul:

F = (9/5) C + 32

Unde F este temperatura în grade Fahrenheit și C este temperatura în grade Celsius.

Presiune și adâncime

Presiunea absolută P într-un fluid incompresibil precum apa, a cărei densitate constantă este ρ, variază în funcție de adâncimea h ca:

P = P_sau + ρgh

Unde P_sau este presiunea la suprafața liberă a lichidului. Dacă lichidul se află într-un recipient deschis către atmosferă, această presiune este pur și simplu presiunea atmosferică P_ATM, putând scrie atunci:

P = P_ATM + ρgh

Presiunea atmosferică la nivelul mării este de aproximativ 101 kPa. Această relație dintre P și h înseamnă că presiunea crește liniar cu adâncimea..

Exercițiul a fost rezolvat

Costul de conducere

Costul lunar C al conducerii unei mașini include un cost lunar fix C_sau plus costul kilometrajului sau kilometrajului efectuat în fiecare lună. Un șofer observă că într-o lună dată costul conducerii a fost de 380 USD pentru 480 de mile, iar în luna următoare a fost de 460 USD pentru 800 de mile.

Fie d numărul de mile parcurse lunar de către șofer, cu datele furnizate, găsiți:

a) Variația liniară între C și d.

b) Cât ar costa pe lună să conduci mașina într-o călătorie de 1.500 de mile?

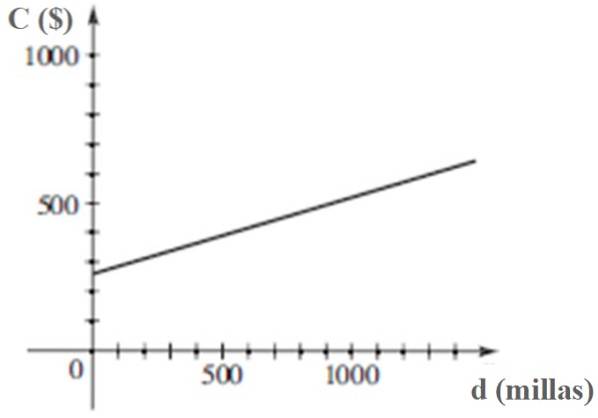
c) Graficul lui C versus d.

Solutie la

Să presupunem că variabilele au o relație dată de:

C = C_sau + Anunț

Unde A și C_sau sunt constante de determinat. A este panta liniei care reprezintă grafic relația dintre C și d. Co este tăierea cu axa verticală, costul fix lunar pe care șoferul trebuie să îl plătească pentru simplul fapt de a avea mașina disponibilă. Aceasta ar putea include, de exemplu, costurile de întreținere și taxele.

Pentru a determina fără echivoc o linie, este necesar să îi cunoaștem panta. Pentru aceasta avem punctele:

P₁: 480 mile, 380 USD

P_Două: 800 mile, 460 dolari

Aceste puncte, de coordonate (d, C) sau (distanță, cost) sunt analoage punctelor de coordonate (x, y) ale planului cartezian, ce modificări sunt numele. Panta A a liniei este dată de:

A = (C_Două - C₁) / (d_Două - d₁)

A = [(460 - 380) $ / (800 - 480) mile] = (1/4) $ / mile

Panta liniei reprezintă costul pe milă, astfel:

C = C_sau + A.d = Co + (1/4) .d

Pentru a determina costul bazei C_sau Această ecuație este luată și unul dintre punctele despre care știm că îi aparține este substituit, de exemplu P₁:

380 $ = C_sau + [(1/4) $ / milă]. 480 mile → 380 $ = C_sau + 120 USD

C_sau = 260 USD

Acum putem formula modelul de variație liniară ca:

C = 260 + (1/4) d

Soluția b

Costul lunar al deplasării 1500 de mile este:

C = 260 + (1/4) x 1500 USD = 635 USD

Soluția c

Graficul lui C versus d este:

Referințe

1. Baldor. 1977. Algebra elementară. Ediții culturale venezuelene.
2. Hoekenga, C. Ecuații liniare în știință. Recuperat de pe: visionlearning.com.
3. Hoffman, J. Selecția subiectelor de matematică. Volumul 2.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Stewart, J. 2006. Precalcul: Matematică pentru calcul. Al 5-lea. Ediție. Cengage Learning.
6. Zill, D. 1984. Algebră și trigonometrie. Dealul Mcgraw.