
Proprietăți vectorilor liberi, exemple, exerciții
vectori liberi Acestea sunt cele care sunt pe deplin specificate prin amploarea, direcția și simțul lor, fără a fi necesar să se indice un punct de aplicare sau o anumită origine..
Deoarece vectori infiniti pot fi trasați în acest fel, un vector liber nu este o singură entitate, ci un set de vectori paraleli și identici, care sunt independenți de unde sunt..
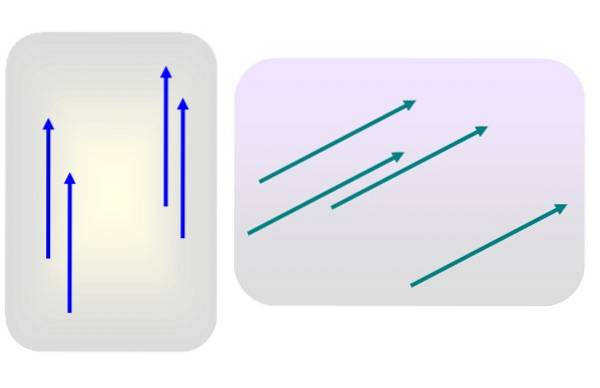
Să spunem că avem mai mulți vectori de magnitudine 3 direcționați vertical în sus sau de magnitudine 5 și înclinați spre dreapta, ca în figura 1.
Niciunul dintre acești vectori nu este aplicat în mod specific în niciun moment. Apoi, oricare dintre vectorii albastri sau verzi este reprezentativ pentru grupul lor respectiv, deoarece caracteristicile lor - modul, direcție și sens - nu se schimbă deloc atunci când sunt transferați într-un alt loc din plan..
Un vector liber este de obicei notat în textul tipărit printr-o literă îngroșată, cu litere mici, de exemplu v. Sau cu litere mici și o săgeată deasupra, dacă este text scris de mână.
Indice articol
- 1 Exemple
- 1.1 Proprietăți și caracteristici
- 2 exerciții rezolvate
- 2.1 -Exercițiunea 1
- 2.2 Exercițiul 2
- 3 Referințe
Exemple
Avantajul vectorilor liberi este că pot fi deplasați prin plan sau prin spațiu și își pot menține proprietățile, deoarece orice reprezentant al mulțimii este la fel de valid.
De aceea, în fizică și mecanică, acestea sunt utilizate frecvent. De exemplu, pentru a indica viteza liniară a unui solid în mișcare, nu este necesar să alegeți un anumit punct de pe obiect. Deci, vectorul viteză se comportă ca un vector liber.
Un alt exemplu de vector liber este perechea de forțe. A pereche Se compune din două forțe de mărime și direcție egale, dar din direcții opuse, aplicate în puncte diferite pe un solid. Efectul unei perechi nu este de a traduce obiectul, ci de a provoca o rotație datorită moment produs.
Figura 2 prezintă câteva forțe aplicate pe un volan. Prin forțe F1 Da FDouă, se creează un cuplu care rotește volanta în jurul centrului și în sensul acelor de ceasornic.
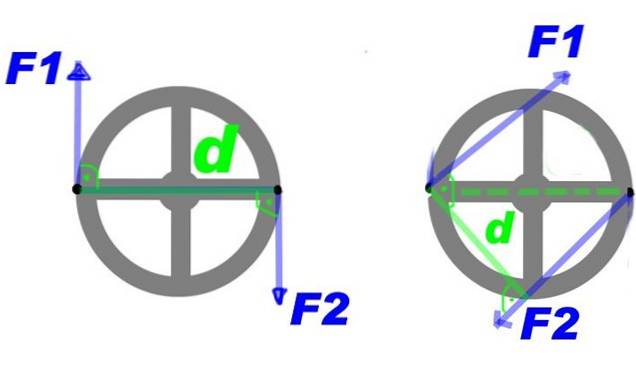
Puteți face unele modificări ale cuplului și puteți obține în continuare același efect de rotație, de exemplu, creșterea forței, dar scăderea distanței dintre ele. Sau mențineți forța și distanța, dar aplicați cuplul pe o altă pereche de puncte de pe volan, adică rotiți cuplul în jurul centrului.
Momentul perechii de forțe sau pur și simplu pereche, este un vector al cărui modul este Fd și este direcționat perpendicular pe planul volantului. În exemplul prezentat prin convenție, rotația în sensul acelor de ceasornic are un sens negativ.
Proprietăți și caracteristici
Spre deosebire de vectorul liber v, vectorii AB Da CD sunt fixe (vezi figura 3), deoarece au un punct de plecare și un punct de sosire specificat. Dar, din moment ce sunt îngăduitori de echipă între ei și, la rândul lor, cu vectorul v, sunt reprezentative pentru vectorul liber v.

Principalele proprietăți ale vectorilor liberi sunt următoarele:
-Orice vector AB (a se vedea figura 2) este, după cum sa spus, reprezentativ pentru vectorul liber v.
-Modulul, direcția și sensul sunt aceleași în orice reprezentant al vectorului liber. În Figura 2, vectorii AB Da CD reprezintă vectorul liber v și sunt orientate spre echipă.
-Având în vedere un punct P în spațiu, este întotdeauna posibil să se găsească un reprezentant al vectorului liber v a cărui origine este în P și reprezentantul menționat este unic. Aceasta este cea mai importantă proprietate a vectorilor liberi și cea care le face atât de versatile.
-Un vector liber nul este notat ca 0 y este ansamblul tuturor vectorilor cărora le lipsește amploarea, direcția și sensul.
-Dacă vectorul AB reprezintă vectorul liber v, apoi vectorul BA reprezintă vectorul liber -v.
-Notarea va fi utilizată V3 pentru a desemna ansamblul tuturor vectorilor liberi ai spațiului și VDouă pentru a desemna toți vectorii liberi ai planului.
Exerciții rezolvate
Cu vectori liberi se pot efectua următoarele operații:
-Sumă
-Scădere
-Înmulțirea scalarului cu un vector
-Produs scalar între doi vectori.
-Produs încrucișat între doi vectori
-Combinație liniară de vectori
Și altele.
-Exercitiul 1
Un student încearcă să înoate dintr-un punct de pe malul unui râu în altul care este chiar opus. Pentru a realiza acest lucru, nimic direct la o viteză de 6 km / h, într-o direcție perpendiculară, totuși curentul are o viteză de 4 km / h care îl deviază.
Calculați viteza rezultată a înotătorului și cât de mult este deviat de curent.
Soluţie
Viteza rezultată a înotătorului este suma vectorială a vitezei sale (față de râu, trasă vertical în sus) și viteza râului (trasă de la stânga la dreapta), care se realizează așa cum se indică în figura de mai jos:
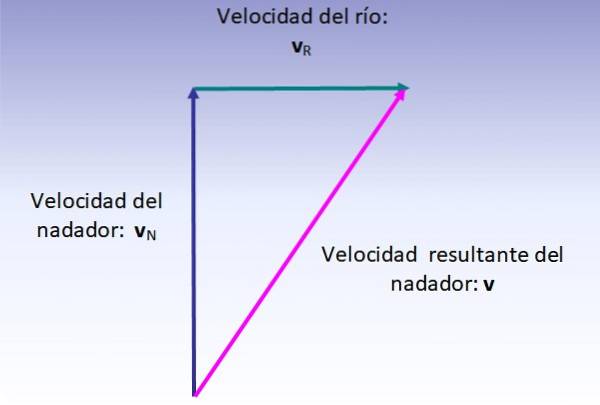
Mărimea vitezei rezultate corespunde hipotenuzei triunghiului dreptunghic prezentat, prin urmare:
v = (6Două + 4Două) ½ km / h = 7,2 km / h
Direcția poate fi calculată folosind unghiul față de perpendicular pe țărm:
α = arctg (4/6) = 33,7º sau 56,3º în raport cu malul.
Exercițiul 2
Găsiți momentul cuplului prezentat în figură:
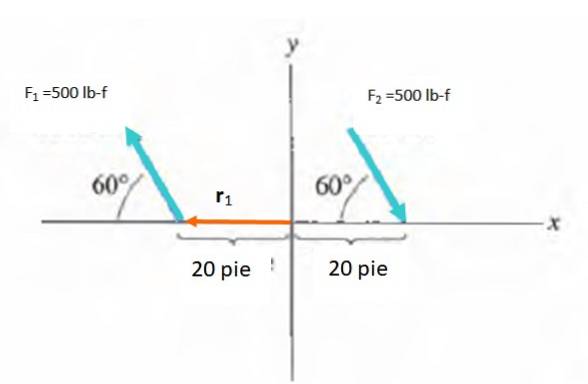
Soluţie
Momentul este calculat prin:
M = r X F
Unitățile momentului sunt lb-f.ft. Deoarece cuplul se află în planul ecranului, momentul este direcționat perpendicular pe acesta, fie în exterior, fie în interior..
Deoarece cuplul din exemplu tinde să rotească obiectul pe care este aplicat (care nu este prezentat în figură) în sensul acelor de ceasornic, acest moment este considerat îndreptat spre interiorul ecranului cu un semn negativ.
Magnitudinea momentului este M = F.d. în a, unde a este unghiul dintre forță și vector r. Trebuie să alegeți un punct cu privire la care să calculați momentul, care este un vector liber. Prin urmare, se alege originea sistemului de referință r merge de la O la punctul de aplicare a fiecărei forțe.
M1 = MDouă = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 lb-f. picior
Momentul net este suma lui M1 si mDouă: -17329,5 lb-f. picior.
Referințe
- Beardon, T. 2011. O introducere la vectori. Adus de la: nrich.maths.org.
- Bedford, 2000. A. Mecanica inginerească: statică. Addison Wesley. 38-52.
- Figueroa, D. Seria: Fizică pentru științe și inginerie. Volumul 1. Cinematică 31-68.
- Fizic. Modulul 8: vectori. Recuperat de la: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecanica pentru ingineri. Static. Ediția a 6-a. Compania Editura Continental. 15-53.
- Calculator de adăugare de vectori. Recuperat de la: 1728.org
- Vectori. Recuperat de la: en.wikibooks.org



Nimeni nu a comentat acest articol încă.