
Conceptul de viteză relativă, exemple, exerciții
viteza relativă a unui obiect este unul care este măsurat în raport cu un observator dat, deoarece un alt observator poate obține o măsurare diferită. Viteza depinde întotdeauna de observatorul care o măsoară.
Prin urmare, viteza unui obiect măsurată de o anumită persoană va fi viteza relativă față de acesta. Un alt observator poate obține o valoare diferită pentru viteză, chiar dacă este același obiect.
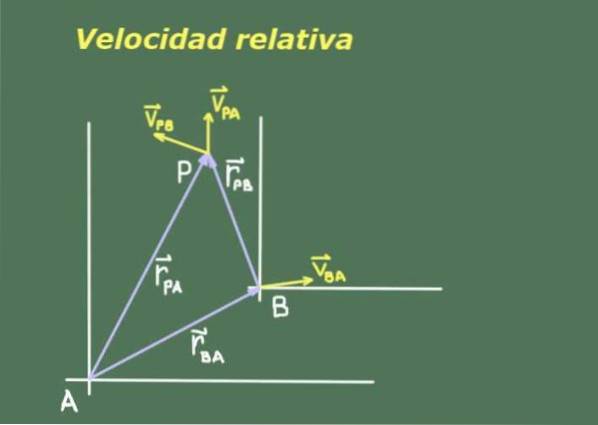
Deoarece doi observatori A și B care se mișcă unul față de celălalt pot avea măsurători diferite ale unui al treilea obiect în mișcare P, este necesar să căutăm o relație între pozițiile și viteza lui P văzute de A și B.
Figura 1 prezintă doi observatori A și B cu sistemele lor de referință, din care măsoară poziția și viteza obiectului P.
Fiecare observator A și B măsoară poziția și viteza obiectului P la un moment dat de timp t. În relativitatea clasică (sau galileană), timpul pentru observatorul A este același ca pentru observatorul B, indiferent de viteza lor relativă.
Acest articol este despre relativitatea clasică, care este valabilă și aplicabilă în majoritatea situațiilor de zi cu zi în care obiectele au viteze mult mai mici decât cea a luminii..
Notăm poziția observatorului B față de A ca rBA. Deoarece poziția este o cantitate vectorială, folosim bold pentru a o indica. Poziția obiectului P față de A este notată ca rPA și cel al aceluiași obiect P față de B rPB.
Indice articol
- 1 Relația dintre pozițiile relative și vitezele
- 1.1 Așa o vede un copil dintr-o mașină în mișcare
- 2 Viteza relativă între motocicletă și mașină
- 2.1-Exercițiul a fost rezolvat
- 3 Referințe
Relația dintre pozițiile relative și vitezele
Există o relație vectorială între aceste trei poziții care poate fi dedusă din reprezentarea figurii 1:
rPA= rPB + rBA
Dacă derivata expresiei anterioare este luată în raport cu timpul t vom obține relația dintre viteza relativă a fiecărui observator:
VPA= VPB + VBA
În expresia anterioară avem viteza relativă a lui P față de A în funcție de viteza relativă a lui P față de B și viteza relativă a lui B față de A.
În mod similar, viteza relativă a lui P față de B poate fi scrisă în funcție de viteza relativă a lui P față de A și viteza relativă a lui A față de B.
VPB= VPA + VAB
Trebuie remarcat faptul că viteza relativă a lui A față de B este egală și contrară cu cea a lui B față de A:
VAB = -VBA
Așa o vede un copil dintr-o mașină în mișcare
O mașină merge pe un drum drept, care merge de la vest la est, cu o viteză de 80 km / h în timp ce în direcția opusă (și din cealaltă bandă) o motocicletă vine cu o viteză de 100 km / h.
Un băiat călătorește pe bancheta din spate a mașinii care vrea să știe viteza relativă a unei motociclete care se apropie de el. Pentru a afla răspunsul, copilul va aplica relațiile pe care tocmai le-a citit în secțiunea anterioară, identificând fiecare sistem de coordonate după cum urmează:
-A este sistemul de coordonate al unui observator pe drum și în ceea ce privește viteza fiecărui vehicul au fost măsurate.
-B este mașina și P este motocicleta.
Dacă doriți să calculați viteza motocicletei P față de mașina B, se va aplica următoarea relație:
VPB= VPA + VAB=VPA - VBA
Luând direcția vest-est ca pozitivă avem:
VPB= (-100 km / h - 80 km / h) eu = -180 km / h eu
Acest rezultat este interpretat după cum urmează: motocicleta se deplasează în raport cu mașina cu o viteză de 180 km / h și direcție -eu, adică de la est la vest.
Viteza relativă între motocicletă și mașină
Motocicleta și mașina s-au încrucișat urmând banda lor. Copilul de pe bancheta din spate a mașinii vede motocicleta îndepărtându-se și acum vrea să știe cât de repede se îndepărtează de el, presupunând că atât motocicleta, cât și mașina mențin aceleași viteze ca înainte de trecere..
Pentru a cunoaște răspunsul, copilul aplică aceeași relație care a fost folosită anterior:
VPB= VPA + VAB=V PA - VBA
VPB= -100 km / h eu - 80 km / h eu = -180 km / h eu
Și acum motocicleta se îndepărtează de mașină cu aceeași viteză relativă cu care se apropia înainte să treacă..
Aceeași motocicletă din partea 2 este returnată menținând aceeași viteză de 100 km / h, dar schimbându-și direcția. Adică, mașina (care continuă cu o viteză de 80 km / h) și motocicleta se deplasează ambele într-o direcție pozitivă est-vest..
La un moment dat, motocicleta trece pe lângă mașină, iar copilul de pe bancheta din spate a mașinii vrea să știe viteza relativă a motocicletei față de el atunci când o vede trecând..
Pentru a obține răspunsul, copilul aplică din nou relațiile de mișcare relativă:
VPB= VPA + VAB=VPA - VBA
VPB= +100 km / h eu - 80 km / h eu = 20 km / h eu
Copilul de pe bancheta din spate urmărește motocicleta depășind mașina cu o viteză de 20 km / h.
-Exercițiul a fost rezolvat
Exercitiul 1
O barcă cu motor traversează un râu care are o lățime de 600 m și curge de la nord la sud. Viteza râului este de 3 m / s. Viteza bărcii față de apa râului este de 4 m / s spre est.
(i) Găsiți viteza bărcii în raport cu malul râului.
(ii) Se indică viteza și direcția bărcii față de uscat.
(iii) Calculați timpul de încrucișare.
(iv) Cât de mult se va deplasa spre sud de la punctul de plecare.
Soluţie
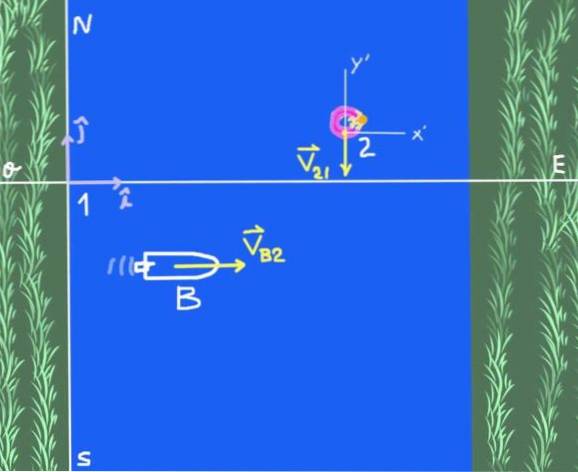
Există două sisteme de referință: sistemul de referință solidar pe malul râului pe care îl vom numi 1 și sistemul de referință 2, care este un observator care plutește pe apa râului. Obiectul de studiu este barca B.
Viteza bărcii în raport cu râul este scrisă în formă vectorială după cum urmează:
VB2 = 4 eu Domnișoară
Viteza observatorului 2 (pluta pe râu) față de observatorul 1 (pe uscat):
Vdouăzeci și unu = -3 j Domnișoară
Vrei să găsești viteza bărcii cu privire la uscat VB1.
VB1 = VB2 + Vdouăzeci și unu
Răspunde i
VB1 = (4 eu - 3 j) Domnișoară
Viteza bărcii va fi modulul vitezei anterioare:
|VB1| = (42 + (-3) 2) ½ = 5 m / s
Răspunsul ii
Și adresa va fi:
θ = arctan (-¾) = -36,87º
Răspunsul iii
Timpul de trecere al bărcii este coeficientul dintre lățimea râului și componenta x a vitezei bărcii față de uscat.
t = (600m) / (4 m / s) = 150 s
Răspuns iv
Pentru a calcula deriva pe care a avut-o barca spre sud, componenta y a vitezei navei față de uscat se înmulțește cu timpul de trecere:
d = -3 j m / s * 150 s = -450 j m
Deplasarea spre sud față de punctul de plecare este de 450m.
Referințe
- Giancoli, D. Fizică. Principii cu aplicații. Ediția a 6-a. Prentice Hall. 80-90
- Resnick, R. (1999). Fizic. Volumul 1. Ediția a treia în limba spaniolă. Mexic. Compañía Editorial Continental S.A. de C.V. 100-120.
- Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7. Ediție. Mexic. Editorii de învățare Cengage. 95-100.
- Wikipedia. Viteza relativă. Recuperat de pe: wikipedia.com
- Wikipedia. Metoda vitezei relative. Recuperat de pe: wikipedia.com



Nimeni nu a comentat acest articol încă.