Accelerația medie cum este calculată și exercițiile rezolvate

accelerare medie la_m Magnitudinea este cea care descrie variația vitezei unei particule în decursul timpului. Este important, deoarece arată variațiile pe care mișcarea le experimentează.

Pentru a exprima această magnitudine în termeni matematici, este necesar să se ia în considerare două viteze și două instante de timp, care sunt respectiv notate ca v₁ și V_Două, si tu₁ si tu_Două.

Combinând valorile conform definiției oferite, se va obține următoarea expresie:

În sistemul internațional SI unitățile pentru a_m va fi m / s^Două, deși vor face și alte unități care implică lungimea pe unitate pătrată.

De exemplu, există km / hs care se citește „kilometru pe oră și pe secundă”. Rețineți că unitatea de timp apare de două ori. Gândindu-ne la un mobil care se mișcă de-a lungul unei linii drepte, înseamnă că pentru fiecare secundă scursă, telefonul își mărește viteza cu 1 km / h. Fie îl scade cu 1 km / h pentru fiecare secundă care trece.

Indice articol

• 1 Accelerație, viteză și viteză
• 2 Cum se calculează accelerarea medie
• 3 semne de accelerație în mișcare unidimensională
• 4 Cadere libera: o miscare cu acceleratie constanta
• 5 Exercițiul a fost rezolvat
  • 5.1 Răspuns
• 6 Referințe

Accelerație, viteză și viteză

Deși accelerația este asociată cu o creștere a vitezei, adevărul este că respectând cu atenție definiția, se dovedește că orice modificare a vitezei implică existența unei accelerații.

Și viteza nu se schimbă întotdeauna în mărime. Se poate întâmpla ca telefonul mobil să își schimbe direcția și să-și păstreze viteza constantă. Totuși, există o accelerare responsabilă a acestei schimbări.

Un exemplu în acest sens este o mașină care face o curbă cu o viteză constantă de 60 km / h. Vehiculul este supus accelerației, care este responsabilă pentru schimbarea direcției de viteză, astfel încât mașina să urmeze curba. Șoferul îl aplică folosind volanul.

O astfel de accelerație este direcționată spre centrul căii curbate, pentru a împiedica mașina să se îndepărteze de ea. Primește numele de accelerație radial sau normal. Dacă accelerația radială ar fi anulată brusc, mașina nu ar mai putea continua să curgă curba și ar continua în linie dreaptă.

O mașină care circulă în jurul unei curbe este un exemplu de mișcare în două dimensiuni, în timp ce atunci când merge în linie dreaptă, mișcarea sa este unidimensională. În acest caz, singurul efect al accelerației este de a schimba viteza mașinii..

Această accelerație se numește accelerație tangenţial. Nu este exclusiv mișcării unidimensionale. Mașina care înconjoară curba la 60 km / h ar putea accelera în același timp la 70 km / h în timp ce o lua. În acest caz, șoferul trebuie să utilizeze atât volanul, cât și pedala de accelerație..

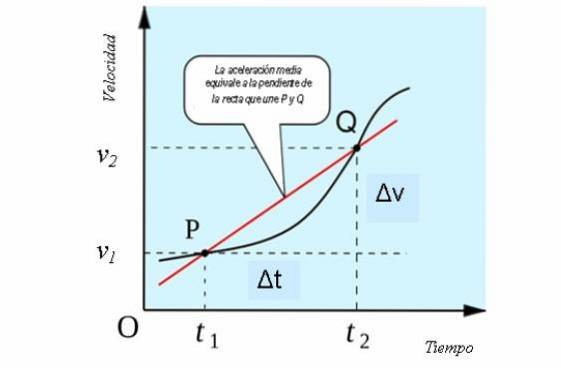
Dacă luăm în considerare o mișcare unidimensională, accelerația medie are o interpretare geometrică similară cu cea a vitezei medii, ca panta liniei secante care intersectează curba în punctele P și Q ale graficului viteză vs. timp..

Acest lucru poate fi văzut în următoarea figură:

Cum se calculează accelerația medie

Să vedem câteva exemple pentru a calcula accelerația medie în diferite situații:

I) La un moment dat, un mobil care se deplasează de-a lungul unei linii drepte are o viteză de + 25 km / h și 120 de secunde mai târziu are o altă viteză de -10 km / h. Care a fost accelerația medie?

Răspuns

Deoarece mișcarea este unidimensională, notația vectorială poate fi eliminată, caz în care:

v_sau = +25 km / h = +6,94 m / s

v_F = -10 km / h = - 2,78 m / s

Δt = 120 s

Ori de câte ori aveți un exercițiu cu magnitudini mixte ca acesta, în care există ore și secunde, este necesar să transmiteți toate valorile aceleași unități.

Fiind o mișcare unidimensională, notația vectorială a fost eliminată.

II) Un ciclist călătorește spre est cu o rată de 2,6 m / s și 5 minute mai târziu merge spre sud cu 1,8 m / s. Găsiți-i accelerația medie.

Răspuns

Miscarea nu este unidimensional, prin urmare se folosește notația vectorială. Vectorii unitari eu Da j indicați direcțiile împreună cu următoarea convenție de semnare, facilitând calculul:

• Nord: +j
• Sud: -j
• Est: +eu
• Vest: -eu

v_Două = - 1,8 j Domnișoară

v₁ = + 2,6 eu Domnișoară

Δt = 5 minute = 300 secunde

Semne de accelerație în mișcare unidimensională

Ca întotdeauna cu magnitudini medii sau medii, informațiile furnizate sunt globale. Nu oferă detalii despre ceea ce s-a întâmplat cu telefonul mobil în fiecare moment al timpului, totuși ceea ce contribuie este încă valoros pentru descrierea mișcării.

Folosind semnele atât ale vitezei, cât și ale accelerației, este posibil să știm dacă un telefon mobil care se deplasează pe o linie dreaptă accelerează sau încetinește. În ambele situații, accelerația este prezentă, deoarece viteza se schimbă.

Iată câteva considerații interesante cu privire la semnele acestor două cantități:

• Viteza medie și accelerația, ambele cu același semn, înseamnă că, la nivel global, mobilul merge din ce în ce mai repede.
• Viteza și accelerația cu semne diferite sunt semnul unui mobil care a fost destul de frânat.

De obicei, se crede că ori de câte ori este o accelerație negativă, mobilul frânează. Acest lucru este adevărat dacă viteza telefonului mobil este pozitivă. Dar dacă este negativă, viteza crește de fapt.

Ca întotdeauna când studiați mișcarea, gândiți-vă la cazuri speciale. De exemplu, ce se întâmplă când accelerația medie este zero? Înseamnă că mobilul și-a păstrat întotdeauna viteza constantă??

Raspunsul este nu. Mobilul ar fi putut varia viteza în intervalul considerat, dar viteza inițială și cea finală au fost aceleași. În prezent, detaliile a ceea ce s-a întâmplat în interval sunt necunoscute, deoarece accelerația medie nu oferă mai multe informații.

Ce se întâmplă dacă accelerația medie la_m este egală cu accelerația la în orice moment al intervalului de timp? Aceasta este o situație foarte interesantă numită Mișcare Rectiliniară Uniformă Varietată sau MRUV pe scurt..

Înseamnă că viteza se schimbă uniform în timp. Prin urmare, accelerația este constantă. În natură există o astfel de mișcare, cu care toată lumea este familiarizată: căderea liberă.

Cădere liberă: o mișcare cu accelerație constantă

Se știe că pământul atrage obiecte spre centrul său și că atunci când cineva este eliberat la o anumită înălțime, experimentează accelerația gravitației, a cărei valoare este aproximativ constantă și egală cu 9,8 m / s^Două aproape de suprafață.

Dacă rezistența la aer nu intervine, mișcarea este verticală și este cunoscută sub numele de cădere liberă. Când accelerația este constantă și se alege t₀ = 0, ecuația pentru accelerația medie devine:

v_F = v₀ + la = gt (v₀= 0)

Unde a = g = 9,8 m / s^Două

Exercițiul a fost rezolvat

Un obiect este scăpat de la o înălțime suficientă. Găsirea vitezei după 1,25 secunde.

Răspuns

v_sau = 0, deoarece obiectul este scăpat, atunci:

v_F = gt = 9,8 x 1,25 m / s = 12,25 m / s, direcționat vertical spre sol. (Direcția verticală descendentă a fost luată ca pozitivă).

Pe măsură ce obiectul se apropie de sol, viteza acestuia crește cu 9,8 m / s pentru fiecare secundă scursă. Masa obiectului nu este implicată. Două obiecte diferite, căzute de la aceeași înălțime și în același timp, dezvoltă aceeași viteză pe măsură ce cad.

Referințe

1. Giancoli, D. Fizică. Principii cu aplicații. Ediția a șasea. Prentice Hall. 21- 35.
2. Resnick, R. (1999). Fizic. Volumul 1. Ediția a treia în limba spaniolă. Mexic. Compañía Editorial Continental S.A. de C.V. 20-34.
3. Serway, R., Jewett, J. (2008). Fizică pentru știință și inginerie. Volumul 1. 7^ma. Ediție. Mexic. Editorii de învățare Cengage. 21-39.