
Concepte, metode, exemple de analiză a plaselor
analiza ochiurilor este o tehnică utilizată pentru rezolvarea circuitelor electrice plate. Această procedură poate apărea, de asemenea, în literatură sub denumirile metodei curenții circuitului sau metoda de curenți de plasă (sau buclă).
Fundamentul acestei și a altor metode de analiză a circuitului electric se află în legile lui Kirchhoff și în legea lui Ohm. La rândul său, legile lui Kirchhoff sunt expresia a două principii foarte importante de conservare în Fizică pentru sisteme izolate: atât sarcina electrică, cât și energia sunt conservate..

Pe de o parte, sarcina electrică este legată de curent, care este sarcina în mișcare, în timp ce într-un circuit, energia este legată de tensiune, care este agentul însărcinat cu efectuarea muncii necesare pentru a menține sarcina în mişcare..
Aceste legi, aplicate unui circuit plat, generează un set de ecuații simultane care trebuie rezolvate pentru a obține valorile curentului sau tensiunii..
Sistemul de ecuații poate fi rezolvat cu tehnici analitice familiare, cum ar fi regula cramerului, care necesită calculul determinanților pentru a obține soluția sistemului.
În funcție de numărul de ecuații, acestea sunt rezolvate folosind un calculator științific sau un software matematic. Pe net există și multe opțiuni disponibile.
Indice articol
- 1 Termeni importanți
- 2 metode
- 2.1 - Pași pentru aplicarea analizei mesh
- 3 exerciții rezolvate
- 3.1 - Exemplul 1
- 3.2 - Exemplul 2
- 4 Referințe
Termeni importanți
Înainte de a explica cum funcționează, vom începe prin a defini acești termeni:
Ramură: secțiune care conține un element de circuit.
Nodul: punct care leagă două sau mai multe ramuri.
Panglică: este orice porțiune închisă a unui circuit, care începe și se termină la același nod.
Plasă: buclă care nu conține nicio altă buclă în interior (plasă esențială).
Metode
Analiza ochiurilor de plasă este o metodă generală utilizată pentru rezolvarea circuitelor ale căror elemente sunt conectate în serie, în paralel sau în mod mixt, adică atunci când tipul de conexiune nu este clar distins. Circuitul trebuie să fie plat sau cel puțin trebuie să fie posibil să-l redesenați ca atare.
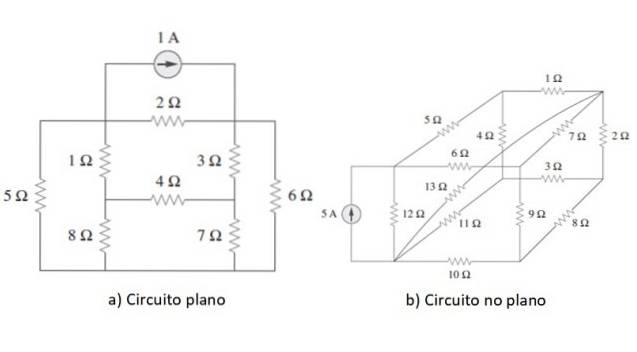
Un exemplu al fiecărui tip de circuit este prezentat în figura de mai sus. Odată ce punctul este clarificat, pentru a începe, vom aplica metoda unui circuit simplu ca exemplu în secțiunea următoare, dar mai întâi vom revizui pe scurt legile lui Ohm și Kirchhoff.
Legea lui Ohm: fi V tensiunea, R rezistență e Eu curentul elementului rezistiv ohmic, în care tensiunea și curentul sunt direct proporționale, rezistența fiind constanta proporționalității:
V = I.R
Legea tensiunii Kirchhoff (LKV): În orice cale închisă parcursă într-o singură direcție, suma algebrică a tensiunilor este zero. Aceasta include tensiuni datorate surselor, rezistențelor, inductoarelor sau condensatoarelor: ∑ E = ∑ Reu. Eu
Legea curentului lui Kirchhoff (LKC): la orice nod, suma algebrică a curenților este zero, ținând cont de faptul că curenților de intrare li se atribuie un semn și cei care părăsesc altul. În acest fel: ∑ I = 0.
Cu metoda curentului mesh, nu este necesar să se aplice legea actuală a lui Kirchhoff, rezultând mai puține ecuații de rezolvat.
- Pași pentru aplicarea analizei mesh
Vom începe prin a explica metoda pentru un circuit cu 2 ochiuri. Procedura poate fi apoi extinsă pentru circuite mai mari.
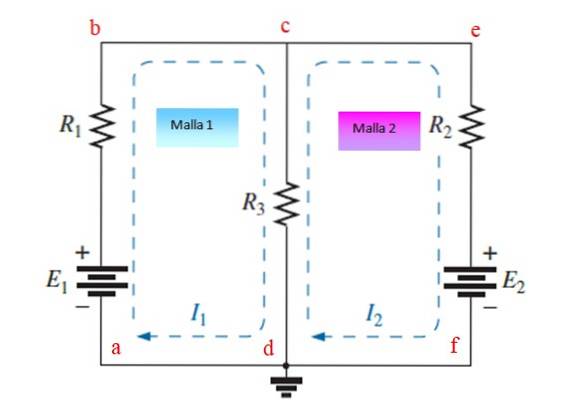
Pasul 1
Atribuiți și trageți curenți independenți pe fiecare rețea, în acest exemplu sunt Eu1 și EuDouă. Pot fi trasate în sensul acelor de ceasornic sau în sens invers acelor de ceasornic.
Pasul 2
Aplicați Legea tensiunilor (LTK) a lui Kirchhoff și legea lui Ohm pe fiecare plasă. Scăderilor potențiale li se atribuie un semn (-) în timp ce creșterile sunt atribuite un semn (+).
Mesh abcda
Începând de la punctul a și urmând direcția curentului, găsim o creștere potențială a bateriei E1 (+), apoi o scădere a R1 (-) și apoi o altă scădere în R3 (-).
Simultan, rezistența R3 este parcurs și de curentul IDouă, dar în direcția opusă, prin urmare reprezintă o creștere (+). Prima ecuație arată astfel:
ȘI1-R1.Eu1 -R3.Eu1 + R3.EuDouă = 0
Apoi se ia în calcul și se regrupează termenii:
- (R1+R3) Eu1 +R3EuDouă = -E1 (Ecuația 1)
Plasa Cefdc
Începând de la punct și și urmând direcția curentului, o potențială cădere se găsește în RDouă (-), o altă scădere ȘIDouă, întrucât curentul intră prin polul + al bateriei și în final o altă cădere R3 (-), În același timp, curentul Eu1 traversează R3 în direcția opusă (+).
A doua ecuație, cu semnele indicate, arată astfel:
- RDouă EuDouă - ȘIDouă -R3 EuDouă +R3 Eu1= 0
R3Eu1 - (RDouă +R3) EuDouă = EDouă (Ecuația 2)
Rețineți că există două ecuații cu cele două necunoscute I1 și euDouă.
Pasul 3
Sistemul de ecuații astfel format este apoi rezolvat.
Exerciții rezolvate
Pentru început, este important să luați în considerare următoarele:
-Curenților de buclă sau curenților de rețea li se poate atribui o adresă arbitrară.
-Fiecare plasă esențială - sau „fereastră” - pe care o are circuitul trebuie să i se atribuie un curent.
-Curenții de plasă sunt notați cu litere mari pentru a-i deosebi de curenții care circulă prin ramuri, deși în unele cazuri curentul care circulă printr-o ramură poate fi același cu cel al ochiurilor.
- Exemplul 1
Găsiți curenții care curg prin fiecare rezistor în circuitul din figura 3, dacă elementele au următoarele valori:
R1 = 20 Ω; RDouă = 30 Ω; R3 = 10 Ω; ȘI1 = 12 V; ȘIDouă = 18 V
Soluţie
În primul rând, este necesar să se atribuie curenții de plasă I1 și euDouă și luați sistemul de ecuații după cum s-a dedus în secțiunea anterioară, apoi înlocuiți valorile date în enunț:
- (R1+R3) Eu1 +R3EuDouă = -E1 (Ecuația 1)
R3Eu1 - (RDouă +R3) EuDouă = EDouă (Ecuația 2)
-
-(20 + 30) Eu1 + 10IDouă = -12
10I1 - (30 +10) IDouă = 18
--
-cincizeciEu1 + 10IDouă = -12
10I1 - 40 euDouă = 18
Deoarece este un sistem de ecuații 2 x 2, poate fi ușor rezolvat prin reducere, înmulțind a doua ecuație cu 5 pentru a elimina necunoscutul Eu1:
-cincizeciEu1 + 10 EuDouă = -12
50I1 - 200 IDouă = 90
-
-190 IDouă= 78
EuDouă = - 78/180 A = - 0,41 A
Imediat curentul se curăță Eu1 din oricare dintre ecuațiile originale:
Eu1 = (18 + 40 IDouă) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A
Semnul negativ din curent EuDouă înseamnă că curentul din rețeaua 2 circulă în direcția opusă celei trase.
Curenții din fiecare rezistor sunt după cum urmează:
Pentru rezistență R1 curentul circulă Eu1 = 0,16 A în sensul tras, prin rezistență RDouă curentul circulă EuDouă = 0,41 A în direcția opusă celei desenate și prin rezistență R3 circula eu3 = 0,16- (-0,41) A = 0,57 A jos.
Soluție de sistem prin metoda lui Cramer
În formă matricială, sistemul poate fi rezolvat după cum urmează:
Pasul 1: Calculați Δ

Pasul 2: Calculați Δ1
Prima coloană este înlocuită de termenii independenți ai sistemului de ecuații, menținând ordinea în care sistemul a fost propus inițial:

Pasul 3: Calculați I1
Eu1 = Δ1/ Δ = 300/1900 = 0,16 A
Pasul 4: Calculați ΔDouă

EuDouă = ΔDouă/ Δ = -780/1900 = -0,41 A
- Exemplul 2
Determinați curentul și tensiunile prin fiecare rezistor din următorul circuit, folosind metoda curenților de plasă:

Soluţie
Cele trei curenți de plasă sunt trase, așa cum se arată în figura următoare, în direcții arbitrare. Acum ochiurile sunt parcurse începând din orice punct:
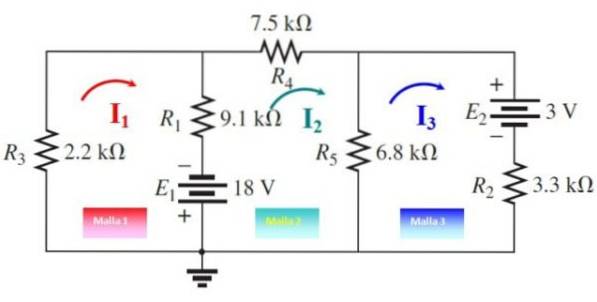
Plasa 1
-9100.I1+18-2200.I1+9100.IDouă= 0
-11300 I1 + 9100.IDouă = -18
Plasa 2
-(7500 + 6800 + 9100) .IDouă + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.IDouă + 6800.I3 = 18
Mesh 3
-(6800 + 3300) I3 + 6800.IDouă - 3 = 0
6800.IDouă - 10100.I3 = 3
Sistem de ecuații
-11300 I1 + 9100.IDouă + 0.I3= -18
9100.I1 - 23400.IDouă + 6800.I3 = 18
0.I1 + 6800.IDouă - 10100.I3 = 3
Deși numerele sunt mari, acesta poate fi rezolvat rapid cu ajutorul unui calculator științific. Amintiți-vă că ecuațiile trebuie ordonate și adăugați zerouri în locurile în care necunoscutul nu apare, așa cum apare aici.
Curenții ochiurilor sunt:
Eu1 = 0,0012 A; EuDouă = -0.00048 A; Eu3 = -0.00062 A
Curenți EuDouă și Eu3 circulă în direcția opusă celei prezentate în figură, deoarece s-au dovedit a fi negative.
Tabel cu curenți și tensiuni în fiecare rezistență
| Rezistență (Ω) | Curent (amperi) | Tensiune = I.R (Volți) |
|---|---|---|
| 9100 | Eu1 -EuDouă = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0,00062 | 2,05 |
| 2200 | 0,0012 | 2,64 |
| 7500 | 0,00048 | 3.60 |
| 6800 | EuDouă -Eu3= -0.00048 - (- 0.00062) = 0.00014 | 0,95 |
Soluția de regulă a lui Cramer
Deoarece sunt un număr mare, este convenabil să folosiți notația științifică pentru a lucra direct cu ei.
Calculul I1
Săgețile colorate din determinantul 3 x 3 indică modul de găsire a valorilor numerice înmulțind valorile indicate. Să începem prin a obține cele din prima paranteză în determinantul Δ:
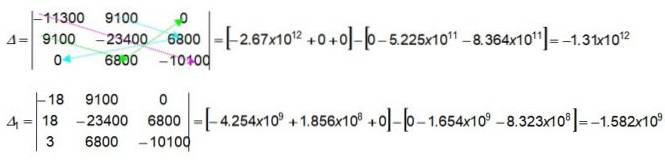
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Imediat obținem a doua paranteză în același determinant, care se lucrează de la stânga la dreapta (pentru această paranteză, săgețile colorate nu au fost desenate în figură). Invităm cititorul să o verifice:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10unsprezece
6800 x 6800 x (-11300) = -5.225 x 10unsprezece
În mod similar, cititorul poate verifica și valorile pentru determinant Δ1.
Important: între ambele paranteze există întotdeauna un semn negativ.
În cele din urmă veți obține curentul Eu1 prin Eu1 = Δ1 / Δ
Eu1 = -1,582 x 109/-1,31 x 1012 = 0,0012 A
Calculul IDouă
Procedura poate fi repetată pentru a calcula EuDouă, în acest caz, pentru a calcula determinantul ΔDouă a doua coloană a determinantului Δ se înlocuiește cu coloana termenilor independenți și se găsește valoarea acestuia, conform procedurii explicate.
Cu toate acestea, deoarece este greoaie din cauza numărului mare, mai ales dacă nu aveți un calculator științific, cel mai ușor lucru este să înlocuiți valoarea Eu1 deja calculat, în următoarea ecuație și clar:
-11300 I1 + 9100.IDouă + 0.I3= -18 → 9100 IDouă= -18 + 11300 I1 → EuDouă = -0.00048 A
Calculul lui I3
Odată cu valorile de Eu1 și EuDouă în mână, cea a Eu3 găsit direct prin substituție.
Referințe
- Alexander, C. 2006. Bazele circuitelor electrice. A treia. Ediție. Mc Graw Hill.
- Boylestad, R. 2011. Introducere în analiza circuitelor.2da. Ediție. Pearson.
- Figueroa, D. (2005). Seria: Fizică pentru știință și inginerie. Volumul 5. Interacțiunea electrică. Editat de Douglas Figueroa (USB).
- García, L. 2014. Electromagnetism. Al 2-lea. Ediție. Universitatea Industrială din Santander.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 2.



Nimeni nu a comentat acest articol încă.