Cum se găsește unghiul unui triunghi?

Există mai multe moduri de a calculați laturile și unghiurile unui triunghi. Acestea depind de tipul de triunghi cu care lucrați.

În această oportunitate, se va arăta cum se calculează laturile și unghiurile unui triunghi dreptunghi, presupunând că anumite date ale triunghiului cu.

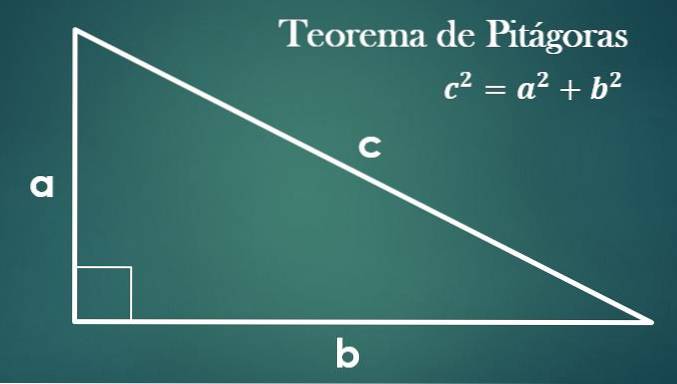
Elementele care vor fi utilizate sunt:

- Teorema lui Pitagora

Având în vedere un triunghi dreptunghiular cu picioarele „a”, „b” și hipotenuză „c”, este adevărat că „c² = a² + b²”.

- Aria unui triunghi

Formula pentru a calcula aria oricărui triunghi este A = (b × h) / 2, unde „b” este lungimea bazei și „h” este lungimea înălțimii.

- Unghiurile unui triunghi

Suma celor trei unghiuri interioare ale unui triunghi este de 180º.

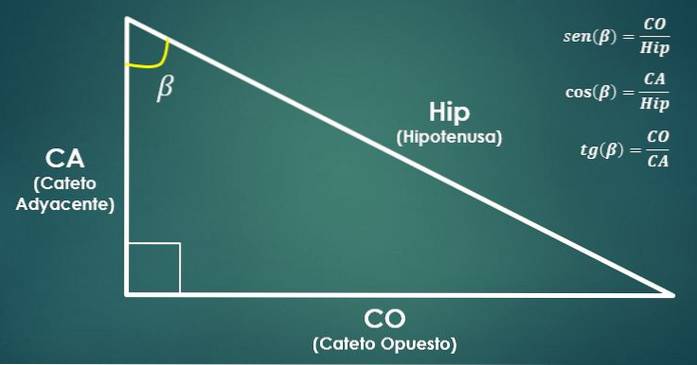
- Funcții trigonometrice:

Luați în considerare un triunghi dreptunghiular. Apoi, funcțiile trigonometrice sinus, cosinus și tangente ale unghiului beta (β) sunt definite după cum urmează:

sin (β) = CO / Hip, cos (β) = CA / Hip și tan (β) = CO / CA.

Cum se găsesc laturile și unghiurile unui triunghi dreptunghiular?

Având în vedere un triunghi dreptunghiular ABC, pot apărea următoarele situații:

1- Cele două picioare sunt cunoscute

Dacă piciorul „a” măsoară 3 cm și piciorul „b” măsoară 4 cm, atunci teorema lui Pitagora este utilizată pentru a calcula valoarea „c”. Înlocuind valorile „a” și „b” obținem acel c² = 25 cm², ceea ce implică faptul că c = 5 cm.

Acum, dacă unghiul β este opus piciorului „b”, atunci sin (β) = 4/5. Aplicând funcția inversă a sinusului, în această ultimă egalitate obținem că β = 53,13º. Două unghiuri interne ale triunghiului sunt deja cunoscute.

Fie θ unghiul care rămâne de cunoscut, apoi 90º + 53,13º + θ = 180º, din care obținem acel θ = 36,87º.

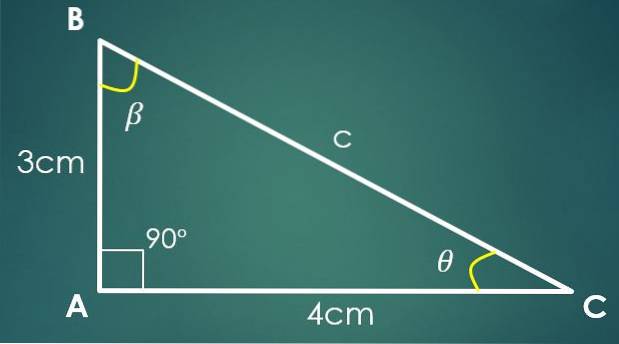
În acest caz, nu este necesar ca laturile cunoscute să fie cele două picioare, important este să cunoaștem valoarea oricărei două laturi.

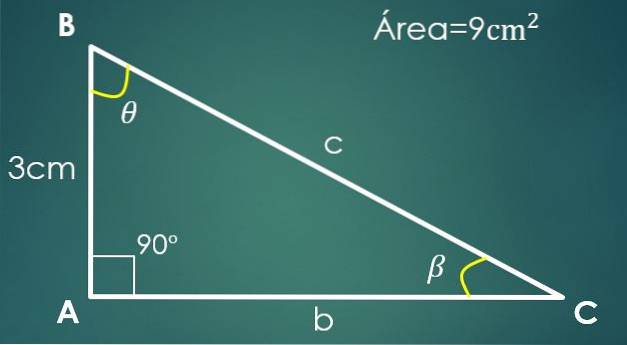
2- Se cunoaște un picior și zona

Fie a = 3 cm piciorul cunoscut și A = 9 cm² aria triunghiului.

Într-un triunghi dreptunghiular, un picior poate fi considerat ca bază și celălalt ca înălțime (deoarece sunt perpendiculare).

Să presupunem că „a” este baza, deci 9 = (3 × h) / 2, din care obținem că celălalt picior are 6 cm. Pentru a calcula hipotenuza, procedăm ca în cazul anterior și obținem că c = √45 cm.

Acum, dacă unghiul β este opus piciorului „a”, atunci sin (β) = 3 / √45. Rezolvând pentru β se obține că valoarea sa este 26,57º. Trebuie doar să cunoaștem valoarea celui de-al treilea unghi θ.

Este satisfăcut că 90º + 26,57º + θ = 180º, din care se concluzionează că θ = 63,43º.

3- Se cunoaște un unghi și un picior

Fie β = 45º unghiul cunoscut și a = 3 cm piciorul cunoscut, unde piciorul „a” este unghiul opus β. Folosind formula tangentă, obținem acel tg (45º) = 3 / CA, din care rezultă că CA = 3 cm.

Folosind teorema lui Pitagora se obține că c² = 18 cm², adică c = 3√2 cm.

Se știe că un unghi măsoară 90º și că β măsoară 45º, de aici se concluzionează că al treilea unghi măsoară 45º.

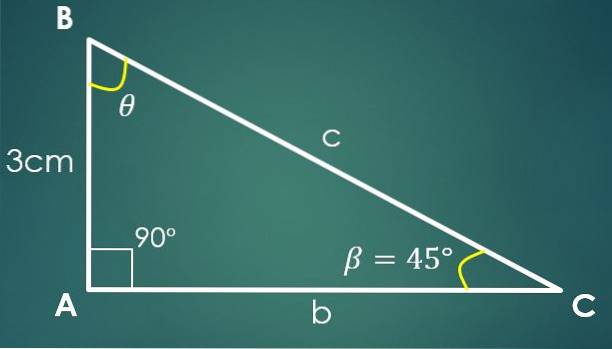
În acest caz, latura cunoscută nu trebuie să fie un picior, poate fi oricare dintre cele trei laturi ale triunghiului.

Referințe

1. Landaverde, F. d. (1997). Geometrie (Reprint ed.). Progres.
2. Leake, D. (2006). Triunghiuri (ed. ilustrată). Heinemann-Raintree.
3. Pérez, C. D. (2006). Precalcul. Pearson Education.
4. Ruiz, Á. Și Barrantes, H. (2006). Geometrii. Tehnologia CR.
5. Sullivan, M. (1997). Precalcul. Pearson Education.
6. Sullivan, M. (1997). Trigonometrie și geometrie analitică. Pearson Education.