
Conceptul de coeficient de restituire, formula, calcul, exemplu

coeficientul de restituire este coeficientul dintre viteza relativă de retragere și viteza relativă de apropiere a două corpuri care se ciocnesc. Când corpurile sunt unite după coliziune, acest coeficient este zero. Și unitatea merită în cazul în care coliziunea este perfect elastică.
Să presupunem că două sfere solide de masă M1 si masa M2 respectiv care suferă o coliziune. Chiar înainte de coliziune sferele aveau viteze V1 Da V2 cu privire la un anumit sistem de referință inerțial. Imediat după coliziune, viteza lor se schimbă la V1 ' Da V2 '.
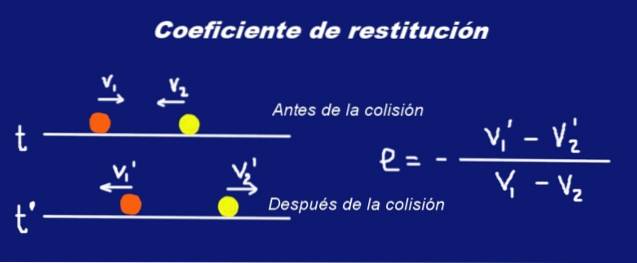
Scrisoarea a fost plasată font bold în viteze pentru a indica faptul că sunt mărimi vectoriale.
Experimentele indică faptul că fiecare coliziune îndeplinește următoarea relație:
V1 ' - V2 '= -și (V1 - V2)
Unde și este un număr real între 0 și 1, numit coeficientul de restituire a coliziunii. Expresia de mai sus este interpretată astfel:
Viteza relativă a două particule înainte de coliziune este proporțională cu viteza relativă a celor două particule după coliziune, constanta proporționalității este (-e), unde e este coeficientul de restituire a coliziunii.
Indice articol
- 1 Pentru ce este coeficientul de restituire?
- 1.1 Elanul
- 1.2 Energia și coeficientul de restituire
- 2 Cum se calculează coeficientul de restituire?
- 3 Exemplu
- 3.1 Soluție
- 4 Referințe
Pentru ce este coeficientul de restituire?
Utilitatea acestui coeficient constă în cunoașterea grad de inelasticitate a unei coliziuni. În cazul în care coliziunea este perfect elastică, coeficientul va fi 1, în timp ce într-o coliziune complet inelastică coeficientul va fi 0, deoarece în acest caz, viteza relativă după coliziune este zero..
Dimpotrivă, dacă se cunoaște coeficientul de restituire a unei coliziuni și viteza particulelor înainte de aceasta, atunci se poate prezice viteza după coliziune..
Impuls
În coliziuni, pe lângă relația care stabilește coeficientul de restituire, există o altă relație fundamentală, care este conservarea impulsului.
Impuls p a unei particule sau a impulsului așa cum se mai numește, este produsul masei M a particulei prin viteza sa V. Adică: impulsul p este o cantitate vectorială.
În coliziuni impulsul liniar P al sistemului este același chiar înainte și imediat după coliziune, deoarece forțele externe sunt neglijabile în comparație cu forțele scurte, dar intense ale interacțiunii interne în timpul coliziunii. Dar conservarea impulsului nu este suficientă P a sistemului pentru a rezolva problema generală a coliziunii.
În cazul menționat anterior, cel al celor două sfere de coliziune ale maselor M1 și M2, conservarea impulsului liniar este scrisă după cum urmează:
M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .
Nu există nicio modalitate de a rezolva problema coliziunii dacă nu se cunoaște coeficientul de restituire. Conservarea impulsului, deși este necesară, este insuficientă pentru a prezice viteza după coliziune.
Când o problemă afirmă că corpurile rămân în mișcare împreună după coliziune, implicit spune că coeficientul de restituire este 0.

Energia și coeficientul de restituire
Cealaltă cantitate fizică importantă implicată în coliziuni este energia. În timpul coliziunilor există schimburi de energie cinetică, energie potențială și alte tipuri de energie, cum ar fi energia termică.
Înainte și după coliziune, energia potențială a interacțiunii este practic nulă, astfel încât echilibrul energetic implică energia cinetică a particulelor înainte și după și o cantitate Î numită energie disipată.
Pentru cele două sfere de masă M1 și M2 care se ciocnesc, echilibrul energetic înainte și după coliziune este scris după cum urmează:
½ M1 V1^ 2 + ½ M2 V2^ 2 = ½ M1 V1 '^ 2 + ½ M2 V2 '^ 2 + Q
Când forțele de interacțiune în timpul coliziunii sunt pur conservatoare, se întâmplă ca energie cinetică totală a particulelor care se ciocnesc este conservată, adică este la fel înainte și după coliziune (Q = 0). Când se întâmplă acest lucru, se spune că coliziunea este perfect elastică..
În caz de coliziuni elastice, nu se disipează energie. În plus, coeficientul de restituire este conform cu: e = 1.
Dimpotrivă, în coliziile inelastice Q ≠ 0 și 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
Pentru ca o problemă de coliziune să fie perfect determinată, este necesar să se cunoască coeficientul de restituire sau, alternativ, cantitatea de energie disipată în timpul coliziunii.
Coeficientul de restituire depinde de natura și tipul de interacțiune dintre cele două corpuri în timpul coliziunii..
La rândul său, viteza relativă a corpurilor înainte de coliziune va defini intensitatea interacțiunii și, prin urmare, influența acesteia asupra coeficientului de restituire..
Cum se calculează coeficientul de restituire?
Pentru a ilustra modul în care se calculează coeficientul de restituire a unei coliziuni, vom lua un caz simplu:
Să presupunem că ciocnirea a două sfere de mase M1 = 1 kg Da M2 = 2 kg deplasarea pe o șină dreaptă fără frecare (ca în figura 1).
Prima sferă lovește cu viteza inițială V1 = 1 m / s pe al doilea care este inițial în repaus, adică V2 = 0 m / s.
După coliziune continuă să se miște astfel: primul se oprește (V1 '= 0 m / s) și al doilea se deplasează spre dreapta cu viteza V2 '= 1/2 m / s.
Pentru a calcula coeficientul de restituire în această coliziune aplicăm relația:
V1 ' - V2 ' = -și ( V1 - V2 )
0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .
Exemplu
În coliziunea unidimensională a celor două sfere ale secțiunii anterioare, a fost calculat coeficientul lor de restituire, rezultând e = ½ .
Deoarece e ≠ 1 coliziunea nu este elastică, adică energia cinetică a sistemului nu este conservată și există o anumită cantitate de energie disipată Q (de exemplu, încălzirea sferelor datorită coliziunii).
Determinați valoarea energiei disipate în Jouli. De asemenea, calculați fracția procentuală de energie disipată.
Soluţie
Energia cinetică inițială a sferei 1 este:
K1i = ½ M1 V1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ J
în timp ce cel al sferei 2 este zero deoarece este inițial în repaus.
Apoi, energia cinetică inițială a sistemului este Ki = ½ J.
După coliziune, numai a doua sferă se mișcă cu viteza V2 '= ½ m / s, deci energia cinetică finală a sistemului va fi:
Kf = ½ M2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J
Adică energia disipată în urma coliziunii este:
Q = Ki - Kf = (½ J - ¼ J) = 1/4 J
Iar fracția de energie disipată în această coliziune se calculează după cum urmează:
f = Q / Ki = ¼ / ½ = 0,5 adică 50% din energia sistemului a fost disipată datorită coliziunii inelastice al cărei coeficient de restituire este 0,5.
Referințe
- Bauer, W. 2011. Fizică pentru inginerie și științe. Volumul 1. Mc Graw Hill.
- Figueroa, D. 2005. Seria: Fizică pentru științe și inginerie. Volumul 1. Cinematica. Editat de Douglas Figueroa (USB).
- Knight, R. 2017. Fizica pentru oamenii de știință și inginerie: o abordare strategică. Pearson.
- Sears, Zemansky. 2016. Fizică universitară cu fizică modernă. 14. Ed. Volumul 1.
- Wikipedia. Cantitatea de mișcare Recuperată de pe: en.wikipedia.org.


Nimeni nu a comentat acest articol încă.