Formule de conducere, calcul, exemple, exerciții

conductanța a unui conductor este definită ca facilitatea pe care trebuie să o treacă curentul electric. Depinde nu numai de materialul utilizat pentru fabricarea acestuia, ci și de geometria sa: lungimea și aria secțiunii transversale.

Simbolul folosit pentru conductanță este G și este inversul rezistenței electrice R, o cantitate puțin mai familiară. Unitatea Sistemului Internațional SI pentru conductanță este inversul ohmului, notat ca Ω^-1 și primește numele de siemens (S).

Alți termeni folosiți în electricitate care sună similar cu conductanța și sunt înrudiți sunt conductivitate si conducere, dar nu trebuie confundate. Primul dintre acești termeni este o proprietate intrinsecă a substanței cu care este realizat conductorul și al doilea descrie fluxul de sarcină electrică prin ea..

Pentru un conductor electric cu secțiune transversală constantă LA, lungime L și conductivitate σ, conductanța este dată de:

G = σ.A / L

Cu cât conductivitatea este mai mare, cu atât conductivitatea este mai mare. De asemenea, cu cât suprafața secțiunii transversale este mai mare, cu atât conductorul este mai ușor să treacă curentul. Dimpotrivă, cu cât lungimea L este mai mare, cu atât conductanța este mai mică, deoarece purtătorii curenți pierd mai multă energie pe trasee mai lungi..

Indice articol

• 1 Cum se calculează conductanța?
  • 1.1 Unități de conductanță
• 2 Exemple
  • 2.1 Conductivitatea și conductanța
  • 2.2 Rezistoare în paralel
• 3 Exerciții
  • 3.1 - Exercițiul 1
  • 3.2 - Exercițiul 2
• 4 Referințe

Cum se calculează conductanța?

Conductanța G pentru un conductor cu secțiune transversală constantă este calculată conform ecuației date mai sus. Acest lucru este important, deoarece dacă secțiunea transversală nu este constantă, trebuie să utilizați calculul integral pentru a găsi atât rezistența, cât și conductanța.

Deoarece este inversul rezistenței, conductanța G poate fi calculată știind că:

G = 1 / R

De fapt, rezistența electrică a unui conductor poate fi măsurată direct cu un multimetru, un dispozitiv care măsoară și curentul și tensiunea..

Unități de conductanță

După cum sa menționat la început, unitatea de conductanță în sistemul internațional este Siemens (S). Se spune că un conductor are o conductanță de 1 S dacă curentul prin el crește cu 1 amper pentru fiecare volt de diferență de potențial.

Să vedem cum este posibil acest lucru prin legea lui Ohm, dacă este scris în termeni de conductanță:

V = I.R = I / G

Unde V este diferența de tensiune sau potențial între capetele conductorului e Eu intensitatea curentului. În ceea ce privește aceste mărimi, formula arată astfel:

G = I / V

În trecut, unitatea pentru conductanță era mho (ohm scris invers) notat ca as, care este un omega capital inversat. Această notație a fost depreciată și a fost înlocuită de siemens în onoarea inginerului și inventatorului german Ernst Von Siemens (1816-1892), pionier al telecomunicațiilor, dar ambele sunt total echivalente.

1 mho = 1 siemens = 1 A / V (ampere / volt)

În alte sisteme de măsurare statsiemens (statS) (în sistemul cgs sau centimetru-gram-secundă) și absiemens (abS) (sistem electromagnetic cgs) cu „s” la final, fără a indica singular sau plural, deoarece provin dintr-un nume propriu.

Unele echivalențe

1 statS = 1.11265 x 10 ^-12 siemens

1 abS = 1 x 10⁹ siemens

Exemple

După cum sa menționat anterior, având rezistență, conductanța este imediat cunoscută atunci când se determină valoarea inversă sau reciprocă. În acest fel, o rezistență electrică de 100 ohmi este echivalentă cu 0,01 siemens, de exemplu.

Iată încă două exemple de utilizare a conductanței:

Conductivitatea și conductanța

Sunt termeni diferiți, așa cum sa indicat deja. Conductivitatea este o proprietate a substanței cu care este realizat conductorul, în timp ce conductanța este proprie conductorului.

Conductivitatea poate fi exprimată în termeni de G ca:

σ = G. (L / A)

Iată un tabel cu conductivitățile materialelor conductive utilizate frecvent:

tabelul 1. Conductivitățile, rezistivitățile și coeficientul termic al unor conductori. Temperatura de referință: 20 ºC.

Metal	σ x 106 (Voi)	ρ x 10-8 (Ω.m)	α ºC-1
Argint	62.9	1,59	0,0058
Cupru	56,5	1,77	0,0038
Aur	41,0	2,44	0,0034
Aluminiu	35.4	2,82	0,0039
Tungsten	18.0	5,60	0,0045
Fier	10.0	10.0	0,0050

Rezistoare în paralel

Când aveți circuite cu rezistențe în paralel, uneori este necesar să obțineți rezistența echivalentă. Cunoașterea valorii rezistenței echivalente permite înlocuirea setului de rezistențe cu o singură valoare.

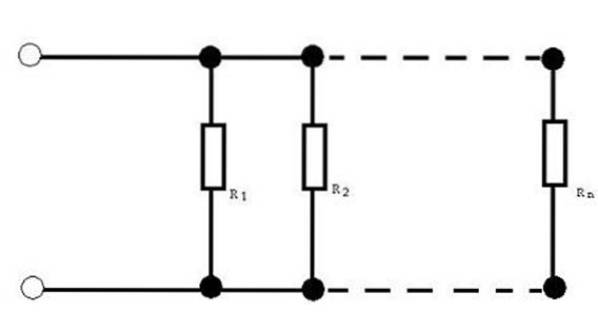
Pentru această configurație a rezistenței, rezistența echivalentă este dată de:

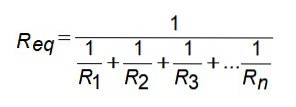
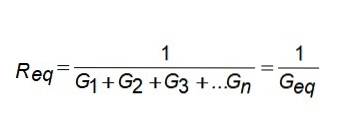
G_echiv = G₁ + G_Două + G₃ +… G_n

Adică, conductanța echivalentă este suma conductanțelor. Dacă doriți să cunoașteți rezistența echivalentă, inversați rezultatul.

Instruire

- Exercitiul 1

a) Scrieți legea lui Ohm în termeni de conductanță.

b) Aflați conductanța unui fir de tungsten de 5,4 cm lungime și 0,15 mm în diametru.

c) Acum un curent de 1,5 A este trecut prin fir. Care este diferența de potențial între capetele acestui conductor?

Solutie la

Din secțiunile precedente trebuie să:

V = I / G

G = σ.A / L

Înlocuind-o pe cea din urmă în prima, arată astfel:

V = I /(σ.A/L) = I.L / σ.A

Unde:

-I este intensitatea curentului.

-L este lungimea conductorului.

-σ este conductivitatea.

-A este aria secțiunii transversale.

Soluția b

Pentru a calcula conductanța acestui fir de tungsten, este necesară conductivitatea acestuia, care se găsește în Tabelul 1:

σ = 18 x10⁶ Voi

L = 5,4 cm = 5,4 x 10^-Două m

D = 0. 15 mm = 0.15 x 10^-3 m

A = π.D^Două / 4 = π. (0,15 x 10^-3 m)^Două / 4 = 1,77 x 10^-8 m^Două

Înlocuind în ecuație avem:

G = σ.A / L = 18 x 10⁶ Da. 1,77 x 10^-8 m^Două / 0,15 x 10^-3 m = 2120,6 S.

Soluția c

V = I / G = 1,5 A / 2120,6 S = 0,71 mV.

- Exercițiul 2

Găsiți rezistența echivalentă în circuitul următor și știind că i_sau = 2 A, calculați i_X și puterea disipată de circuit:

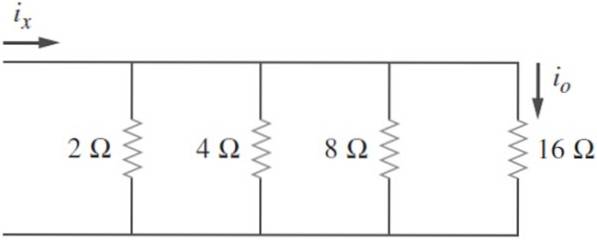
Soluţie

Rezistoarele sunt listate: R₁= 2 Ω; R_Două= 4 Ω; R₃= 8 Ω; R₄= 16 Ω

Apoi, conductanța este calculată în fiecare caz: G₁ = 0,5 Ʊ; G_Două = 0,25 Ʊ; G₃ = 0,125 Ʊ; G₄ = 0,0625 Ʊ

Și, în cele din urmă, se adaugă așa cum s-a indicat anterior, pentru a găsi conductanța echivalentă:

G_echiv = G₁ + G_Două + G₃ +… G_n = 0,5 Ʊ + 0,25 Ʊ + 0,125 Ʊ + 0,0625 Ʊ = 0,9375 Ʊ

Prin urmare R_echiv = 1,07 Ω.

Tensiunea pe R₄ este V₄ = i_sau. R₄ = 2 A. 16 Ω = 32 V, și este același pentru toate rezistențele, deoarece acestea sunt conectate în paralel. Apoi, este posibil să găsiți curenții care curg prin fiecare rezistență:

-eu₁ = V₁ / R₁ = 32 V / 2 Ω = 16 A

-eu_Două = V_Două / R_Două = 32 V / 4 Ω = 8 A

-eu₃ = V₃ / R₃ = 32 V / 8 Ω = 4 A

-eu_X = i₁ +  eu_Două +  eu₃ + eu_sau = 16 + 8 + 4 + 2 A = 30 A

În cele din urmă, puterea disipată P este:

P = (i_X)^Două. R_echiv = 30 A x 1,07 Ω = 32,1 W

Referințe

1. Alexander, C. 2006. Bazele circuitelor electrice. A treia. Ediție. Dealul Mcgraw.
2. Conversie megaampere / milivolt în calculatorul absiemens. Recuperat de pe: pinkbird.org.
3. García, L. 2014. Electromagnetism. Al 2-lea. Ediție. Universitatea Industrială din Santander. Columbia.
4. Knight, R. 2017. Fizica pentru oamenii de știință și inginerie: o abordare strategică. Pearson.
5. Roller, D. 1990. Fizică. Electricitate, magnetism și optică. Volumul II. Editorial Reverté.
6. Wikipedia. Conductanța electrică. Recuperat de pe: es.wikipedia.org.
7. Wikipedia. Siemens. Recuperat de pe: es.wikipedia.org.