
Congruență cifre congruente, criterii, exemple, exerciții
congruenţă, În geometrie, subliniază că, dacă două figuri plane au aceeași formă și dimensiuni, ele sunt congruente. De exemplu, două segmente sunt congruente atunci când lungimile lor sunt egale. La fel, unghiurile congruente au aceeași măsură, chiar dacă nu sunt orientate în același mod în plan..
Termenul „congruență” provine din latină congruente, al cărui sens este corespondența. Astfel, două figuri congruente corespund exact între ele..
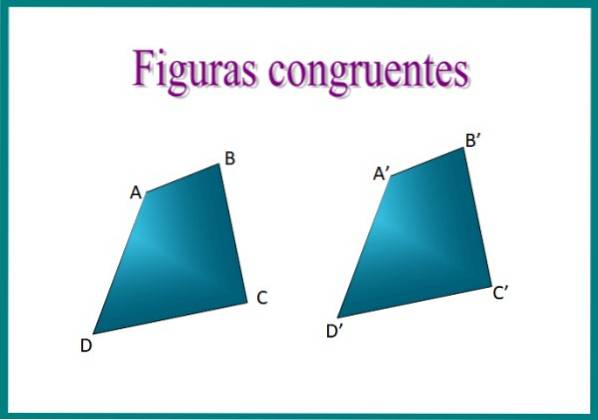
De exemplu, dacă suprapunem cele două patrulatere din imagine, vom constata că sunt congruente, deoarece dispunerea laturilor lor este identică și măsoară la fel.
Prin plasarea patrulaterelor ABCD și A'B'C'D 'una peste alta, cifrele se vor potrivi exact. Părțile potrivite sunt numite laturi omoloage sau corespunzător iar pentru exprimarea congruenței se folosește simbolul ≡. Atunci putem afirma că ABCD ≡ A'B'C'D '.
Indice articol
- 1 Criterii de congruență
- 1.1 Congruență, identitate și similitudine
- 2 Exemple de congruență
- 2.1 - Congruența unghiului
- 2.2 - Congruența triunghiurilor
- 3 exerciții rezolvate
- 3.1 - Exercițiul 1
- 3.2 - Exercițiul 2
- 4 Referințe
Criterii de congruență
Următoarele caracteristici sunt comune poligoanelor congruente:
-Aceeași formă și dimensiune.
-Măsuri identice ale unghiurilor lor.
-Aceeași măsură pe fiecare dintre laturile sale.
În cazul în care doi poligoane în cauză sunt regulate, adică toate laturile și unghiurile interne măsoară la fel, congruența este asigurată atunci când este îndeplinită niste dintre următoarele condiții:
-Laturile sunt congruente
- apoteme au aceeași măsură
- radio din fiecare poligon măsoară egal
Apotema unui poligon regulat este distanța dintre centru și una dintre laturi, în timp ce raza corespunde distanței dintre centru și un vârf sau colț al figurii.
Criteriile de congruență sunt frecvent utilizate, deoarece atât de multe părți și piese de toate tipurile sunt produse în serie și trebuie să aibă aceeași formă și măsurători. În acest fel, ele pot fi ușor înlocuite atunci când este necesar, de exemplu piulițe, șuruburi, foi sau pavajele de pe sol în stradă..

Congruență, identitate și similitudine
Există, de exemplu, concepte geometrice legate de congruență cifre identice si cifre similare, care nu implică neapărat că figurile sunt congruente.
Rețineți că figurile congruente sunt identice, totuși patrulaterele din figura 1 ar putea fi orientate în moduri diferite pe plan și să rămână în continuare congruente, deoarece orientarea diferită nu schimbă dimensiunea laturilor sau a unghiurilor lor. În acest caz, acestea ar înceta să fie identice.
Celălalt concept este acela al similitudinii figurilor: două figuri plane sunt similare dacă au aceeași formă și unghiurile lor interne măsoară la fel, deși dimensiunea figurilor poate fi diferită. Dacă acesta este cazul, cifrele nu sunt congruente.
Exemple de congruență
- Congruența unghiului
După cum am indicat la început, unghiurile congruente au aceeași măsură. Există mai multe modalități de a obține unghiuri congruente:
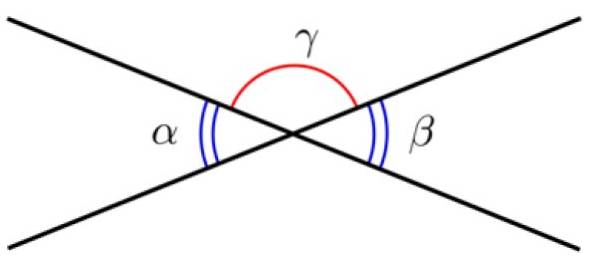
Exemplul 1
Două linii cu un punct comun definesc două unghiuri, numite Unghiuri opuse de vârf. Aceste unghiuri au aceeași măsură, prin urmare sunt congruente.
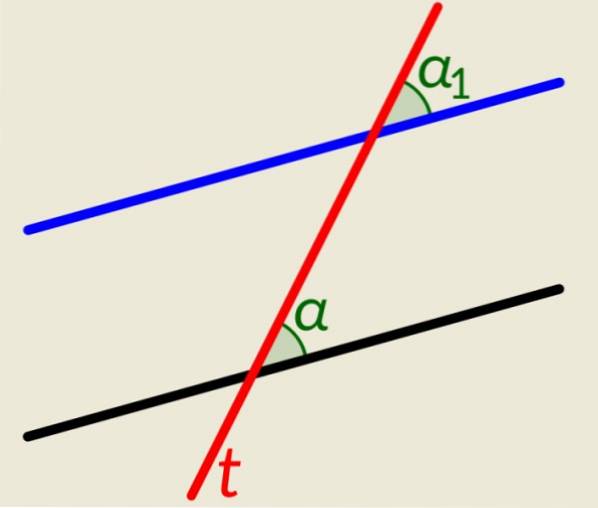
Exemplul 2
Există două linii paralele plus o linie t care îi intersectează pe amândoi. Ca și în exemplul anterior, atunci când această linie intersectează paralelele, generează unghiuri congruente, una pe fiecare linie pe partea dreaptă și alte două pe partea stângă. Figura arată α și α1, în dreapta liniei t, care sunt congruente.
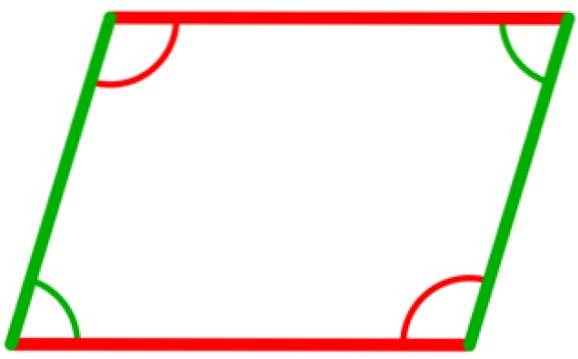
Exemplul 3
Într-un paralelogram există patru unghiuri interioare, care sunt congruente două la două. Acestea sunt cele care se află între vârfurile opuse, așa cum se arată în figura următoare, în care cele două unghiuri în verde sunt congruente, precum și cele două unghiuri în roșu.
- Congruența triunghiurilor
Două triunghiuri de aceeași formă și dimensiune sunt congruente. Pentru a verifica acest lucru, există trei criterii care pot fi examinate în căutarea congruenței:
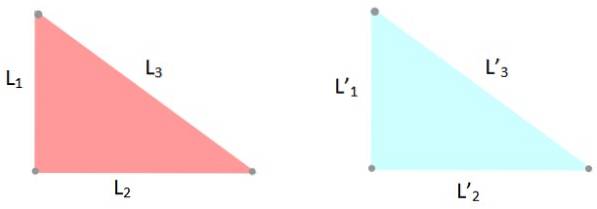
-Criteriul LLL: cele trei laturi ale triunghiurilor au aceleași măsurători, deci L1 = L '1; LDouă = L 'Două și eu3 = L '3.
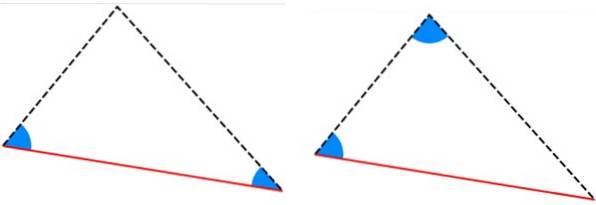
-Criteriile ALA și AAL: triunghiurile au două unghiuri interioare egale, iar latura dintre acele unghiuri are aceeași măsură.
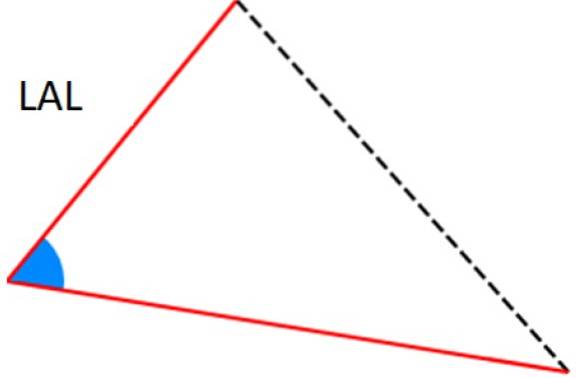
-Criteriul LAL: două dintre laturi sunt identice (corespunzătoare) și între ele există același unghi.
Exerciții rezolvate
- Exercitiul 1
Două triunghiuri sunt prezentate în figura următoare: ΔABC și ΔECF. Se știe că AC = EF, că AB = 6 și că CF = 10. Mai mult, unghiurile ∡BAC și ∡FEC sunt congruente, iar unghiurile ∡ACB și ∡FCB sunt, de asemenea, congruente..
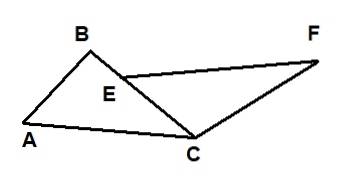
Atunci lungimea segmentului BE este egală cu:
(i) 5
(ii) 3
(iii) 4
(iv) 2
(v) 6
Soluţie
Deoarece cele două triunghiuri au o latură egală cu AC = EF cuprinsă între unghiurile egale ∡BAC = ∡CEF și ∡BCA = ∡CFE, se poate spune că cele două triunghiuri sunt congruente conform criteriului ALA.
Adică ΔBAC ≡ ≡CEF, deci trebuie să:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Dar segmentul de calculat este BE = BC - EC = 10 - 6 = 4.
Deci, răspunsul corect este (iii).
- Exercițiul 2
Trei triunghiuri sunt prezentate în figura de mai jos. Se știe, de asemenea, că cele două unghiuri indicate măsoară fiecare 80º și că segmentele AB = PD și AP = CD. Găsiți valoarea unghiului X indicat în figură.
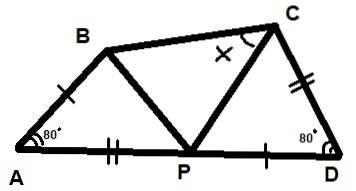
Soluţie
Trebuie să aplicați proprietățile triunghiurilor, care sunt detaliate pas cu pas.
Pasul 1
Începând cu criteriul de congruență al triunghiului LAL, se poate afirma că triunghiurile BAP și PDC sunt congruente:
ΔBAP ≡ ΔPDC
Pasul 2
Cele de mai sus conduc la afirmarea faptului că BP = PC, deci triunghiul ΔBPC este isoscel și ∡PCB = ∡PBC = X.
Pasul 3
Dacă numim unghiul BPC γ, rezultă că:
2x + γ = 180º
Pasul 4
Și dacă numim unghiurile APB și DCP β și α unghiurile ABP și DPC, avem:
α + β + γ = 180º (deoarece APB este un unghi plan).
Pasul 5
Mai mult, α + β + 80º = 180º prin suma unghiurilor interne ale triunghiului APB.
Pasul 6
Combinând toate aceste expresii avem:
α + β = 100º
Pasul 7
Prin urmare:
γ = 80º.
Pasul 8
În cele din urmă rezultă că:
2X + 80º = 180º
Cu X = 50º.
Referințe
- Baldor, A. 1973. Geometria planului și spațiului. Cultural Central American.
- Fundația CK-12. Poligoane congruente. Recuperat din: ck 12.org.
- Bucurați-vă de matematică. Definiții: Raza (poligon). Recuperat de pe: gustolasmatematicas.com.
- Math Open Reference. Testarea poligoanelor pentru congruență. Recuperat de pe: mathopenref.com.
- Wikipedia. Congruență (geometrie). Recuperat de pe: es.wikipedia.org.
- Zapata, F. Triunghiuri, istorie, elemente, clasificare, proprietăți. Recuperat de pe: lifeder.com.


Nimeni nu a comentat acest articol încă.