Constanta de semnificație, calcul și exemple de integrare

constantă a integrării Este o valoare adăugată la calculul antiderivativelor sau integralelor, servește la reprezentarea soluțiilor care alcătuiesc primitivul unei funcții. Exprimați o ambiguitate inerentă în care orice funcție are un număr infinit de primitivi.

De exemplu, dacă luăm funcția: f (x) = 2x + 1 și obținem antiderivarea acesteia:

∫ (2x + 1) dx = x^Două + X + C ; Unde C este constantă a integrării și reprezintă grafic translația verticală între posibilitățile infinite ale primitivului. Este corect să spunem că (x^Două + x) este A din primitivele lui f (x).

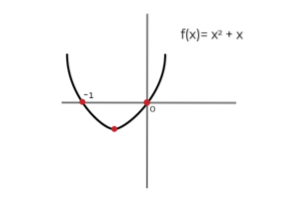
În același mod putem defini un (x^Două + X + C ) ca primitivă a lui f (x).

Indice articol

• 1 Proprietate inversă
• 2 Integrala nedefinită
• 3 Alte semnificații ale constantei integrării
• 4 Cum se calculează constanta integrării?
• 5 Exemple
  • 5.1 Exemplul 1
  • 5.2 Exemplul 2
  • 5.3 Exemplul 3
• 6 Exerciții propuse
  • 6.1 Exercițiul 1
  • 6.2 Exercițiul 2
  • 6.3 Exercițiul 3
  • 6.4 Exercițiul 4
• 7 Referințe

Proprietate inversă

Se poate observa că prin derivarea expresiei (x^Două + x) se obține funcția f (x) = 2x + 1. Aceasta se datorează proprietății inverse existente între derivarea și integrarea funcțiilor. Această proprietate permite obținerea de formule de integrare pornind de la diferențiere. Ceea ce permite verificarea integralelor prin aceleași derivate.

Cu toate acestea (x^Două + x) nu este singura funcție a cărei derivată este egală cu (2x + 1).

1. d (X^Două + x) / dx = 2x + 1
2. d (X^Două + x + 1) / dx = 2x + 1
3. d (X^Două + x + 2) / dx = 2x + 1
4. d (X^Două + x + 3) / dx = 2x + 1
5. d (X^Două + X + C) / dx = 2x + 1

Unde 1, 2, 3 și 4 reprezintă primitive particulare ale lui f (x) = 2x + 1. În timp ce 5 reprezintă integralul nedefinit sau primitiv al lui f (x) = 2x + 1.

Primitivele unei funcții sunt realizate prin antiderivare sau proces integral. Unde F va fi o primitivă a lui f dacă următoarele sunt adevărate

• y = ∫ f (x) dx = F (x) + C; C = constantă a integrării
• F '(x) = f (x)

Se poate observa că o funcție are o singură derivată, spre deosebire de primitivele sale infinite rezultate din integrare.

Integrala nedefinită

 ∫ f (x) dx = F (x) + C

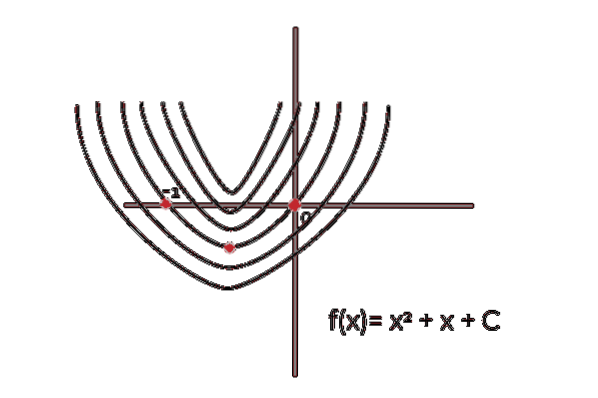
Corespunde unei familii de curbe cu același model, care experimentează incongruență în valoarea imaginilor fiecărui punct (x, y). Fiecare funcție care îndeplinește acest model va fi o primitivă individuală și setul tuturor funcțiilor este cunoscut sub numele de integral nedefinit.

Valoarea constantă a integrării va fi cea care diferențiază fiecare funcție în practică.

constantă a integrării sugerează o deplasare verticală în toate graficele reprezentând primitivele unei funcții. Unde se observă paralelismul dintre ele și faptul că C este valoarea deplasării.

Conform practicilor comune, constantă a integrării este notată cu litera „C” după un addend, deși în practică nu contează dacă se adaugă sau se scade constanta. Valoarea sa reală poate fi găsită în diferite moduri în funcție de diferite condiții inițiale.

Alte semnificații ale constantei integrării

S-a vorbit deja despre cum constantă a integrării se aplică în ramura calcul integral; Reprezentând o familie de curbe care definesc integralul nedefinit. Dar multe alte științe și ramuri au atribuit valori foarte interesante și practice ale constantă a integrării, care au facilitat dezvoltarea de studii multiple.

În fizic constanta integrării poate lua valori multiple în funcție de natura datelor. Un exemplu foarte comun este cunoașterea funcției V (t) care reprezintă viteză a unei particule versus timp t. Se știe că la calcularea unei primitive de V (t) se obține funcția R (t) care reprezintă poziţie particula versus timp.

constantă a integrării va reprezenta valoarea poziției inițiale, adică la momentul t = 0.

În mod similar, dacă funcția este cunoscută A (t)  care reprezintă accelerare a particulei versus timp. Primitivul lui A (t) va avea ca rezultat funcția V (t), unde constantă a integrării va fi valoarea vitezei inițiale V₀.

În economie, prin obținerea prin intermediul integrării a primitivei unei funcții de cost. constantă a integrării va reprezenta costuri fixe. Și atâtea alte aplicații care merită calcul diferențial și integral.

Cum se calculează constanta integrării?

Pentru a calcula constantă a integrării, va fi întotdeauna necesar să cunoaștem condiții inițiale. Care sunt responsabili pentru definirea careia dintre primitivele posibile este cea corespunzătoare.

În multe aplicații este tratată ca o variabilă independentă la timpul (t), unde constanta C ia valorile care definesc condiții inițiale a cazului particular.

Dacă luăm exemplul inițial: ∫ (2x + 1) dx = x^Două + X + C

O condiție inițială validă poate fi condiția ca graficul să treacă printr-o anumită coordonată. De exemplu, se știe că primitivul (x^Două + X + C) trece prin punctul (1, 2)

F (x) = x^Două + X + C; aceasta este soluția generală

F (1) = 2

Înlocuim soluția generală în această egalitate

F (1) = (1)^Două + (1) + C = 2

De unde rezultă cu ușurință asta C = 0

În acest fel, primitivul corespunzător pentru acest caz este F (x) = x^Două + X

Există mai multe tipuri de exerciții numerice cu care funcționează constante de integrare. De fapt, calculul diferențial și integral nu încetează să fie aplicat în investigațiile curente. La diferite niveluri academice pot fi găsite; din calculul inițial, prin fizică, chimie, biologie, economie, printre altele.

Se vede și în studiul ecuatii diferentiale, unde constantă a integrării Poate lua diferite valori și soluții, aceasta datorită multiplelor derivări și integrări care sunt efectuate în această materie.

Exemple

Exemplul 1

1. Un tun situat la 30 de metri înălțime trage un proiectil vertical în sus. Se știe că viteza inițială a proiectilului este de 25 m / s. Decide:

• Funcția care definește poziția proiectilului în raport cu timpul.
• Momentul zborului sau instantaneu când particula lovește solul.

Se știe că într-o mișcare rectilinie uniform variată, accelerația este o valoare constantă. Acesta este cazul lansării proiectilului, unde accelerația va fi gravitațională

g = - 10 m / s^Două

Se mai știe că accelerația este a doua derivată a poziției, ceea ce indică o dublă integrare în rezoluția exercițiului, obținându-se astfel două constante de integrare.

A (t) = -10

V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C₁

Condițiile inițiale ale exercițiului indică faptul că viteza inițială este V₀ = 25 m / s. Aceasta este viteza în momentul t = 0. În acest fel, este satisfăcut că:

V (0) = 25 = -10 (0) + C₁   Da C₁ = 25

Funcția de viteză fiind definită

V (t) = -10t + 25; Similitudinea cu formula MRUV (V_F = V₀ + a x t)

Într-un mod omolog, procedăm la integrarea funcției de viteză pentru a obține expresia care definește poziția:

R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5t^Două + 25t + C_Două

R (t) = -5t^Două + 25t + C_Două  (primitiv de poziție)

Se cunoaște poziția inițială R (0) = 30 m. Apoi se calculează primitivul particular al proiectilului.

R (0) = 30m = -5 (0)^Două + 25 (0) + C_Două . Unde C_Două = 30

Prima secțiune este rezolvată de atunci R (t) = -5t^Două + 25t + 30  ; Această expresie este omologă cu formula de deplasare în MRUV R (t) = R₀ + V₀t - gt^Două/Două

Pentru a doua secțiune, ecuația pătratică trebuie rezolvată: -5t^Două + 25t + 30 = 0

Deoarece aceasta condiționează particula pentru a ajunge la sol (poziția = 0)

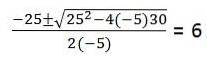
De fapt, ecuația de gradul 2 ne oferă 2 soluții T: 6, -1. Valoarea t = -1 este ignorată deoarece este unități de timp al căror domeniu nu include numere negative.

În acest fel, a doua secțiune este rezolvată în cazul în care timpul de zbor este egal cu 6 secunde.

Exemplul 2

2. Găsiți f (x) primitiv care îndeplinește condițiile inițiale:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Cu informațiile derivatei a doua f "(x) = 4, începe procesul de antiderivare

f '(x) = ∫f "(x) dx

∫4 dx = 4x + C₁

Apoi, cunoscând starea f '(2) = 2, procedăm:

4 (2) + C₁ = 2

C₁ = -6 și f '(x) = 4x - 8

Procedați în același mod pentru a doua constantă a integrării

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x^Două - 8x + C_Două

Se cunoaște condiția inițială f (0) = 7 și continuăm:

2 (0)^Două - 8 (0) + C_Două = 7

C_Două = 7 și f (x) = 2x^Două - 8x + 7

• f "(x) = x^Două ; f '(0) = 6; f (0) = 3

În mod similar cu problema anterioară, definim primele derivate și funcția originală din condițiile inițiale.

f '(x) = ∫f "(x) dx

∫ (x^Două) dx = (x³/ 3) + C₁

Cu condiția f '(0) = 6 procedăm:

(0³/ 3) + C₁ = 6; Unde₁ = 6 și f '(x) = (x³/ 3) + 6

Apoi al doilea constantă a integrării

f (x) = ∫f '(x) dx

∫ [(x³/ 3) + 6] dx = (x⁴/ 12) + 6x + C_Două

Se cunoaște condiția inițială f (0) = 3 și continuăm:

[(0)⁴/ 12] + 6 (0) + C_Două = 3; Unde_Două = 3

Astfel obținem particularitatea primitivă

f (x) = (X⁴/ 12) + 6x + 3

Exemplul 3

3. Definiți funcțiile primitive având în vedere derivatele și un punct pe grafic:

• dy / dx = 2x - 2 care trece prin punctul (3, 2)

Este important să ne amintim că derivatele se referă la panta liniei tangente la curbă într-un punct dat. Unde nu este corect să presupunem că graficul derivatei atinge punctul indicat, deoarece acesta aparține graficului funcției primitive.

În acest fel, exprimăm ecuația diferențială după cum urmează:

dy = (2x - 2) dx  ; atunci când aplicăm criteriile anti-derivare avem:

∫dy = ∫ (2x - 2) dx

y = x^Două - 2x + C

Aplicarea condiției inițiale:

2 = (3)^Două - 2 (3) + C

C = -1

Este obținut: f (x) = x^Două - 2x - 1

• dy / dx = 3x^Două - 1 Ce trece prin punctul (0, 2)

Exprimăm ecuația diferențială după cum urmează:

dy = (3x^Două - 1) dx  ; atunci când aplicăm criteriile anti-derivare avem:

 ∫dy = ∫ (3x^Două - 1) dx

y = x³ - x + C

Aplicarea condiției inițiale:

2 = (0)^Două - 2 (0) + C

C = 2

Este obținut: f (x) = x³ - x + 2

Exerciții propuse

Exercitiul 1

1. Găsiți f (x) primitiv care îndeplinește condițiile inițiale:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Exercițiul 2

2. Un balon care urcă cu o viteză de 16 ft / s aruncă o pungă de nisip de la o înălțime de 64 ft deasupra nivelului solului.

• Definiți timpul de zbor
• Ce va fi vectorul V_F când am lovit podeaua?

Exercițiul 3

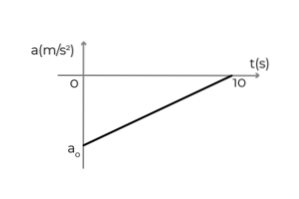
3. Figura arată graficul de accelerare-timp al unei mașini care se deplasează în direcția pozitivă a axei x. Mașina circula cu o viteză constantă de 54 km / h când șoferul a acționat frâna pentru a opri în 10 secunde. A determina:

• Accelerația inițială a mașinii
• Viteza mașinii la t = 5s
• Deplasarea mașinii în timpul frânării

Exercițiul 4

4. Definiți funcțiile primitive având în vedere derivatele și un punct pe grafic:

• dy / dx = x care trece prin punctul (-1, 4)
• dy / dx = -x^Două + 1 Ce trece prin punctul (0, 0)
• dy / dx = -x + 1 care trece prin punctul (-2, 2)

Referințe

1. Calcul integral. Integrala nedefinită și metodele de integrare. Wilson, Velásquez Bastidas. Universitatea Magdalena 2014
2. Stewart, J. (2001). Calculul unei variabile. Transcendentalii timpurii. Mexic: Thomson Learning.
3. Jiménez, R. (2011). Matematica VI. Calcul integral. Mexic: Pearson Education.
4. Fizică I. Mc Graw hill