
Exemple de coordonate dreptunghiulare și exerciții rezolvate
coordonate dreptunghiulare sau cartezian sunt cele care se obțin prin proiectarea ortogonală pe cele trei axe carteziene X, Y, Z un punct situat în spațiul tridimensional.
Axele carteziene sunt linii orientate reciproc perpendiculare între ele. În sistemul de coordonate carteziene, fiecărui punct din spațiu i se atribuie trei numere reale care sunt coordonatele sale dreptunghiulare.
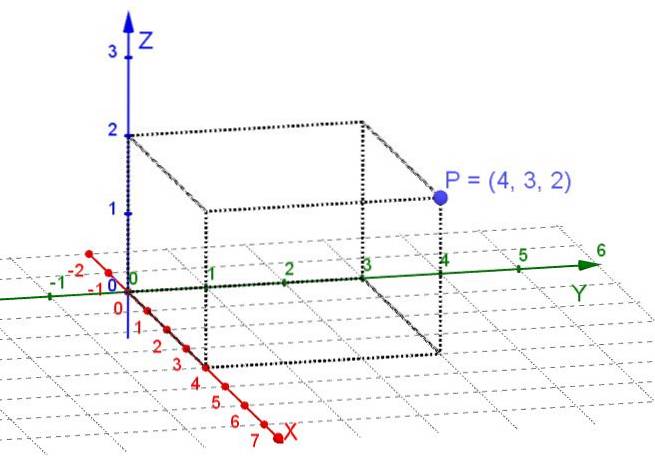
Un plan este un subspatiu al spatiului tridimensional. În cazul luării în considerare a punctelor de pe un plan, atunci este suficient să alegeți o pereche de axe perpendiculare X, Y ca sistem cartezian. Atunci fiecărui punct al planului i se atribuie două numere reale care sunt coordonatele sale dreptunghiulare.
Indice articol
- 1 Originea coordonatelor dreptunghiulare
- 2 Planul cartezian
- 2.1 Distanța dintre două puncte
- 2.2 Expresia analitică a unei linii
- 3 Exemple
- 3.1 Exemplul 1
- 3.2 Exemplul 2
- 4 exerciții rezolvate
- 4.1 Exercițiul 1
- 4.2 Exercițiul 2
- 5 Referințe
Originea coordonatelor dreptunghiulare
Coordonatele dreptunghiulare au fost inițial propuse de matematicianul francez René Descartes (1596 și 1650), motiv pentru care sunt numite carteziene.
Cu această idee a lui Descartes, punctelor planului și spațiului li se atribuie numere, astfel încât figurile geometrice au o ecuație algebrică asociată și teoremele geometrice clasice pot fi dovedite algebric. Cu coordonatele carteziene, se naște geometria analitică.
Avionul cartezian
Dacă într-un plan se aleg două linii perpendiculare care se intersectează într-un punct O; și dacă, în plus, fiecărei linii i se atribuie o direcție și o scară numerică între punctele echidistante succesive, atunci există un sistem cartesian sau plan în care fiecare punct al planului este asociat cu o pereche ordonată de două numere reale care sunt proiecțiile lor respectiv pe axele X și Y.
Punctele A = (3, 2); B = (- 2, 3); C = (- 2, -3) și D = (3, -3) sunt reprezentate în plan cartezian așa cum se arată mai jos:
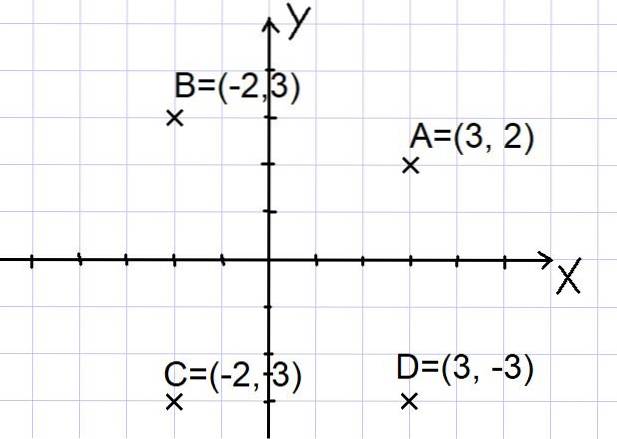
Rețineți că cele două axe X și Y împart planul în patru sectoare numite cadrane. Punctul A este în primul cadran, B este în al doilea cadran, C este în al treilea cadran, iar punctul D este în al patrulea cadran..
Distanța dintre două puncte
Distanța dintre două puncte A și B pe plan cartezian este lungimea segmentului care le unește. Această distanță poate fi calculată analitic după cum urmează:
d (A, B) = √ (Bx - Ax) ^ 2 + (By - Ay) ^ 2)
Formula de mai sus se obține prin aplicarea teoremei lui Pitagora.
Aplicând această formulă punctelor A, B din figura 2 avem:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
Adică d (A, B) = 5,10 unități. Rețineți că distanța a fost obținută fără a fi necesară măsurarea cu o riglă, a fost urmată o procedură complet algebrică.
Expresia analitică a unei linii
Coordonatele dreptunghiulare permit reprezentarea analitică a obiectelor geometrice fundamentale precum punctul și linia. Două puncte A și B definesc o singură linie. Panta liniei este definită ca coeficientul dintre diferența coordonatelor Y ale punctului B minus A, împărțit la diferența coordonatelor X ale punctului B minus A:
panta = (By - Ay) / (Bx - Axe)
Orice punct P de coordonate (x, y) care aparține liniei (AB) trebuie să aibă aceeași pantă:
panta = (y - Ay) / (x - Ax)
Ecuația care se obține prin intermediul egalității pantelor este reprezentarea analitică sau algebrică a liniei care trece prin punctele A și B:
(y - Ay) / (x - Ax) = (By - Ay) / (Bx - Ax).
Dacă luăm pentru A și B coordonatele dreptunghiulare din figura 2 avem:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
În acest caz particular, avem o linie cu o pantă negativă -⅕, ceea ce înseamnă că, localizând pe un punct de pe linie și mărind coordonata x cu o unitate, coordonata y scade cu 0,2 unități.
Cea mai obișnuită modalitate de a scrie ecuația liniei în plan este cu coordonata y ștearsă în funcție de variabila x:
y = - (1/5) x + 13/5
Exemple
Exemplul 1
Obțineți prin metode analitice distanța dintre punctele C și A, fiind coordonatele dreptunghiulare ale lui C = (-2, -3) și cele ale lui A = (3,2).
Formula pentru distanța euclidiană dintre aceste două puncte este scrisă astfel:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
Înlocuind coordonatele lor dreptunghiulare corespunzătoare avem:
d (A, C) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7.07
Exemplul 2
Obțineți ecuația liniei care trece prin punctul C al coordonatelor (-2, -3) și punctul P al coordonatelor (2, 0).
În primul rând, se obține panta liniei CP:
panta = (0 - (- 3)) / (2 - (-2)) = ¾
Orice punct Q de coordonate dreptunghiulare generice (x, y) care aparține liniei CP trebuie să aibă aceeași pantă:
panta = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
Cu alte cuvinte, ecuația liniei CP este:
(y +3) / (x +2) = ¾
O modalitate alternativă de a scrie ecuația liniei CP este rezolvarea pentru y:
y = ¾ x - 3/2
Exerciții rezolvate
Exercitiul 1
Obțineți coordonatele dreptunghiulare ale punctului de intersecție dintre liniile y = - (1/5) x + 13/5 și linia y = ¾ x - 3/2.
Soluție: Prin definiție, punctul de intersecție al celor două linii împarte aceleași coordonate dreptunghiulare. Prin urmare, coordonatele y la punctul de intersecție sunt identice pentru ambele linii:
-(1/5) x + 13/5 = ¾ x - 3/2
ceea ce duce la următoarea expresie:
(¾ + ⅕) x = 13/5 +3/2
rezolvând suma fracțiilor obținem:
19/20 x = 41/10
Rezolvarea pentru x:
x = 82/19 = 4,32
Pentru a obține interceptarea y, valoarea x obținută este substituită în oricare dintre linii:
y = ¾ 4,32 - 3/2 = 1,74
Aceasta înseamnă că liniile date se intersectează în punctul I al coordonatelor I = (4.32, 1.74).
Exercițiul 2
Obțineți ecuația circumferinței care trece prin punctul R al coordonatelor dreptunghiulare (3, 4) și care își are centrul la originea coordonatelor.
Soluție: Raza R este distanța de la punctul R la originea O a coordonatelor (0, 0).
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3 - 0) ^ 2 + (4 - 0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
Adică este un cerc de rază 5 centrat la (0,0).
Orice punct P (x, y) de pe circumferință trebuie să aibă aceeași distanță 5 de centru (0, 0), astfel încât să poată fi scris:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
Și anume:
√ (x ^ 2 + y ^ 2) = 5
Pentru a elimina rădăcina pătrată, ambii membri ai egalității sunt pătrate, obținând:
x ^ 2 + y ^ 2 = 25
Care este ecuația circumferinței.
Acest exemplu ilustrează puterea sistemului de coordonate dreptunghiulare, care permite determinarea obiectelor geometrice, cum ar fi circumferința, fără a fi nevoie să folosiți hârtie, creion și busolă. Circumferința solicitată a fost determinată exclusiv prin metode algebrice.
Referințe
- Arfken G și Weber H. (2012). Metode matematice pentru fizicieni. Un ghid cuprinzător. Ediția a VII-a. Academic Press. ISBN 978-0-12-384654-9
- Calcul cc. S-au rezolvat probleme de coordonate dreptunghiulare. Recuperat de la: calculo.cc
- Weisstein, Eric W. „Coordonatele carteziene”. De la MathWorld-A Wolfram Web. Recuperat de pe: mathworld.wolfram.com
- wikipedia. Sistemul de coordonate carteziene. Recuperat de pe: en.wikipedia.com



Nimeni nu a comentat acest articol încă.