
Derivate succesive (cu exerciții rezolvate)
derivate succesive sunt derivatele unei funcții după a doua derivată. Procesul de calculare a derivatelor succesive este următorul: avem o funcție f, pe care o putem obține și astfel putem obține funcția derivată f '. Putem deriva din nou această derivată a lui f, obținând (f ')'.
Această nouă funcție se numește a doua derivată; toate derivatele calculate din a doua sunt succesive; Acestea, numite și ordine superioară, au aplicații excelente, cum ar fi oferirea de informații despre graficul unei funcții, testul celei de-a doua derivate pentru extreme relative și determinarea seriilor infinite.

Indice articol
- 1 Definiție
- 1.1 Exemplul 1
- 1.2 Exemplul 2
- 2 Viteză și accelerație
- 2.1 Exemplul 1
- 2.2 Exemplul 2
- 3 Aplicații
- 3.1 Derivarea implicită
- 3.2 Exemplu
- 3.3 Extreme relative
- 3.4 Exemplu
- 3.5 Seria Taylor
- 3.6 Exemplu
- 4 Referințe
Definiție
Folosind notația lui Leibniz, avem că derivata unei funcții „y” față de „x” este dy / dx. Pentru a exprima a doua derivată a „y” folosind notația lui Leibniz, scriem după cum urmează:

În general, putem exprima derivate succesive după cum urmează cu notația lui Leibniz, unde n reprezintă ordinea derivatei.

Alte notații utilizate sunt următoarele:
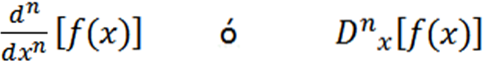
Câteva exemple în care putem vedea diferitele notații sunt:
Exemplul 1
Obțineți toate derivatele funcției f definite de:
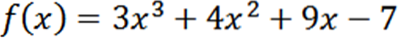
Folosind tehnicile obișnuite de derivare, considerăm că derivata lui f este:

Repetând procesul putem obține a doua derivată, a treia derivată și așa mai departe.
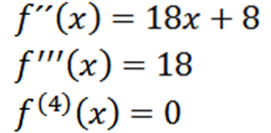
Rețineți că a patra derivată este zero și derivata zero este zero, deci avem:

Exemplul 2
Calculați a patra derivată a următoarei funcții:
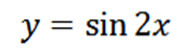
Derivând funcția dată avem ca rezultat:
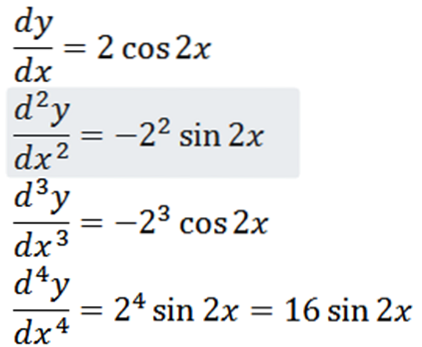
Viteza și accelerația
Una dintre motivațiile care au condus la descoperirea derivatului a fost căutarea definiției vitezei instantanee. Definiția formală este următoarea:
Fie y = f (t) o funcție al cărei grafic descrie traiectoria unei particule într-un moment t, atunci viteza sa la un moment t este dată de:

Odată ce viteza unei particule este obținută, putem calcula accelerația instantanee, care este definită după cum urmează:
Accelerarea instantanee a unei particule a cărei cale este dată de y = f (t) este:

Exemplul 1
O particulă se mișcă de-a lungul unei linii în funcție de funcția de poziție:

Unde „y” este măsurat în metri și „t” în secunde.
- În ce moment este viteza sa 0?
- În ce moment este accelerarea sa 0?
Când derivăm funcția de poziție "y", avem viteza și accelerația acesteia, respectiv, date de:

Pentru a răspunde la prima întrebare, este suficient să se determine când funcția v devine zero; aceasta este:
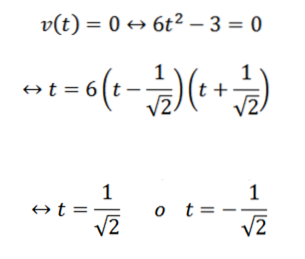
Continuăm cu următoarea întrebare în mod similar:

Exemplul 2
O particulă se mișcă de-a lungul unei linii conform următoarei ecuații de mișcare:

Determinați „t, y” și „v” când a = 0.
Știind că viteza și accelerația sunt date de

Procedăm la obținerea și obținerea:

Făcând un = 0, avem:
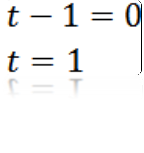
De unde putem deduce că valoarea lui t astfel încât a este egală cu zero este t = 1.
Apoi, evaluând funcția de poziție și funcția de viteză la t = 1, avem:

Aplicații
Derivare explicită
Derivații succesivi pot fi obținuți și prin derivare implicită.
Exemplu
Având în vedere următoarea elipsă, găsiți „y”:

Derivând implicit cu privire la x, avem:
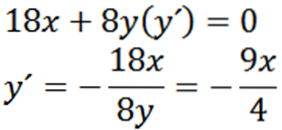
Apoi, implicit, derivarea cu privire la x ne oferă:

În cele din urmă, avem:
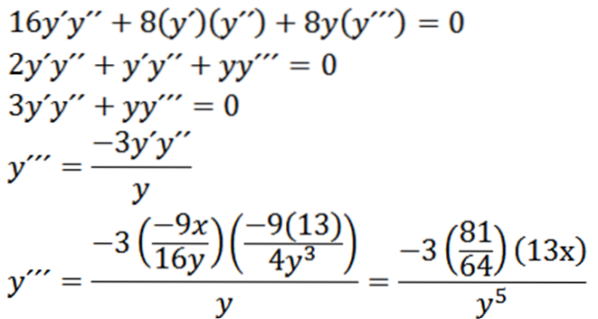
Extreme relative
O altă utilizare pe care o putem da derivatelor de ordinul doi este în calculul extremelor relative ale unei funcții.
Criteriul primei derivate pentru extreme locale ne spune că, dacă avem o funcție continuă f într-un interval (a, b) și există un c care aparține intervalului menționat astfel încât f 'dispare în c (adică, c este un punct critic), poate apărea unul din cele trei cazuri:
- Dacă f '(x)> 0 pentru orice x aparținând lui (a, c) și f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
- Dacă f '(x) < 0 para cualquier x perteneciente a (a,c) y f'(x)>0 pentru x aparținând lui (c, b), atunci f (c) este un minim local.
- Dacă f '(x) are același semn în (a, c) și în (c, b), implică faptul că f (c) nu este o extremă locală.
Folosind criteriul celei de-a doua derivate putem ști dacă un număr critic al unei funcții este un maxim local sau un minim, fără a trebui să vedem care este semnul funcției în intervalele menționate anterior..
Al doilea criteriu de deriva ne spune că dacă f '(c) = 0 și că f "(x) este continuu în (a, b), se întâmplă că dacă f" (c)> 0 atunci f (c) este local minim și dacă f "(c) < 0 entonces f(c) es un máximo local.
Dacă f "(c) = 0, nu putem concluziona nimic.
Exemplu
Având în vedere funcția f (x) = x4 + (4/3) x3 - 4xDouă, găsiți maxime și minime relative ale lui f aplicând al doilea criteriu derivat.
Mai întâi calculăm f '(x) și f "(x) și avem:
f '(x) = 4x3 + 4xDouă - 8x
f "(x) = 12xDouă + 8x - 8
Acum, f '(x) = 0 dacă și numai dacă 4x (x + 2) (x - 1) = 0, iar acest lucru se întâmplă când x = 0, x = 1 sau x = - 2.
Pentru a determina dacă numerele critice obținute sunt extreme relative, este suficient să se evalueze la f "și să se observe astfel semnul acestuia.
f "(0) = - 8, deci f (0) este un maxim local.
f "(1) = 12, deci f (1) este un minim local.
f "(- 2) = 24, deci f (- 2) este un minim local.
Seria Taylor
Fie o funcție definită după cum urmează:
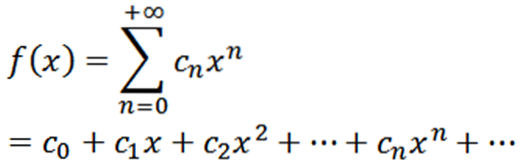
Această funcție are o rază de convergență R> 0 și are derivate de toate ordinele în (-R, R). Derivații succesivi ai lui f ne oferă:
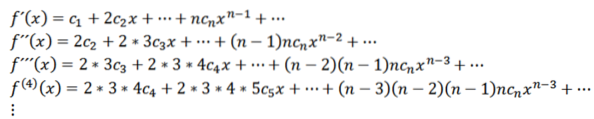
Luând x = 0, putem obține valorile lui cn pe baza derivatelor sale după cum urmează:
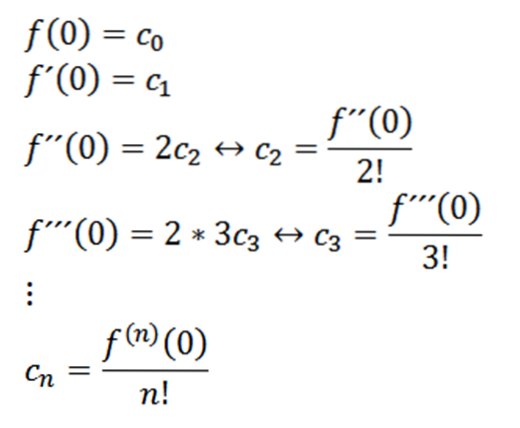
Dacă luăm n = 0 ca funcție f (adică f ^ 0 = f), atunci putem rescrie funcția după cum urmează:
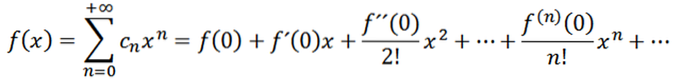
Acum să considerăm funcția ca o serie de puteri la x = a:
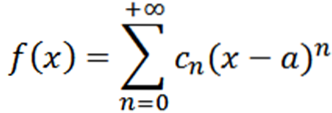
Dacă vom efectua o analiză analogă celei anterioare, am avea că putem scrie funcția f ca:
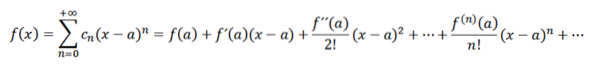
Aceste serii sunt cunoscute sub numele de serii Taylor de la f la a. Când a = 0 avem cazul particular care se numește seria Maclaurin. Acest tip de serie are o mare importanță matematică în special în analiza numerică, deoarece datorită acestora putem defini funcții în computere precum eX , sin (x) și cos (x).
Exemplu
Obțineți seria Maclaurin pentru eX.
Rețineți că dacă f (x) = eX, apoi f(n)(x) = eX și f(n)(0) = 1, deci seria dvs. Maclaurin este:
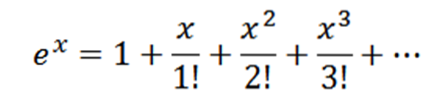
Referințe
- Frank Ayres, J. și Mendelson, E. (s.f.). Calcul 5ed. Mc Graw Hill.
- Leithold, L. (1992). Calculul cu geometrie analitică. HARLA, S.A.
- Purcell, E. J., Varberg, D. și Rigdon, S. E. (2007). Calcul. Mexic: Pearson Education.
- Saenz, J. (2005). Calcul diferențial. Ipotenuză.
- Saenz, J. (s.f.). Calcul integral. Ipotenuză.
Nimeni nu a comentat acest articol încă.