dilatarea superficială Este expansiunea care are loc atunci când un obiect experimentează variații ale suprafeței sale datorită variației temperaturii. Se datorează caracteristicilor materialului sau formei sale geometrice. Dilatarea predomină în două dimensiuni în aceeași proporție.
De exemplu, într-o foaie, atunci când există o modificare a temperaturii, suprafața foii este cea care suferă cea mai mare modificare din cauza expansiunii termice..
Tabla din figura precedentă își mărește lățimea și lungimea în mod apreciabil atunci când este încălzită de radiația solară. Dimpotrivă, ambele scad semnificativ atunci când este răcit din cauza scăderii temperaturii ambiante..
Din acest motiv, atunci când plăcile sunt instalate pe podea, marginile nu trebuie să se lipească între ele, dar ar trebui să existe un spațiu numit rost de dilatare..
În plus, acest spațiu este umplut cu un amestec special care are un anumit grad de flexibilitate, împiedicând crăparea plăcilor din cauza presiunilor puternice pe care le poate produce expansiunea termică..
Indice articol
Într-un material solid atomii își mențin pozițiile relative mai mult sau mai puțin fixe în jurul unui punct de echilibru. Cu toate acestea, datorită agitației termice, acestea oscilează întotdeauna în jurul aceluiași.
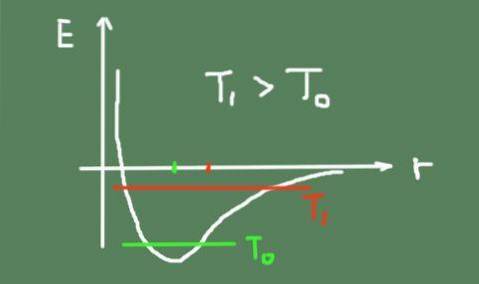
Pe măsură ce temperatura crește, oscilația termică crește, de asemenea, provocând schimbarea pozițiilor de oscilație mijlocie. Acest lucru se datorează faptului că potențialul de legare nu este tocmai parabolic și are asimetrie în jurul valorii minime.
Mai jos este o figură care prezintă energia legăturii chimice în funcție de distanța interatomică. Se arată, de asemenea, energia totală a oscilației la două temperaturi și modul în care se mișcă centrul oscilației..
Pentru a măsura dilatația suprafeței, pornim de la o zonă inițială A și o temperatură inițială T, a obiectului a cărei dilatație urmează să fie măsurată..
Să presupunem că respectivul obiect este o foaie a zonei A, iar grosimea sa este mult mai mică decât rădăcina pătrată a zonei A. Foaia este supusă unei variații de temperatură ΔT, astfel încât temperatura sa finală odată ce echilibrul termic cu sursa de căldură a fost stabilit, va fi T '= T + ΔT.
În timpul acestui proces termic, suprafața se va schimba, de asemenea, la o nouă valoare A '= A + ΔA, unde ΔA este schimbarea lungimii. Astfel, coeficientul de expansiune a suprafeței σ este definit ca fiind coeficientul dintre variația relativă a zonei pe unitate de variație a temperaturii.
Următoarea formulă definește coeficientul de expansiune a suprafeței σ:
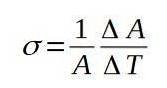
Coeficientul de expansiune a suprafeței σ este practic constant pe o gamă largă de valori de temperatură.
Prin definiția lui σ, dimensiunile sale sunt inverse ale temperaturii. Unitatea este de obicei ° C-1.
În continuare vom oferi o listă a coeficientului de expansiune superficială pentru unele materiale și elemente. Coeficientul este calculat la presiunea atmosferică normală pe baza unei temperaturi ambiante de 25 ° C, iar valoarea sa este considerată constantă în intervalul ΔT de la -10 ° C la 100 ° C.
Unitatea coeficientului de expansiune a suprafeței va fi (° C)-1
- Oțel: σ = 24 ∙ 10-6 (° C)-1
- Aluminiu: σ = 46 ∙ 10-6 (° C)-1
- Aur: σ = 28 ∙ 10-6 (° C)-1
- Cupru: σ = 34 ∙ 10-6 (° C)-1
- Alamă: σ = 36 ∙ 10-6 (° C)-1
- Fier: σ = 24 ∙ 10-6 (° C)-1
- Sticlă: σ = (14-18) ∙ 10-6 (° C)-1
- Cuarț: σ = 0,8 ∙ 10-6 (° C)-1
- Diamant: σ = 2 ,, 4 ∙ 10-6 (° C)-1
- Plumb: σ = 60 ∙ 10-6 (° C)-1
- Lemn de stejar: σ = 108 ∙ 10-6 (° C)-1
- PVC: σ = 104 ∙ 10-6 (° C)-1
- Fibra de carbon: σ = -1,6 ∙ 10-6 (° C)-1
- Beton: σ = (16 la 24) ∙ 10-6 (° C)-1
Majoritatea materialelor se întind cu o creștere a temperaturii. Cu toate acestea, unele materiale, cum ar fi fibra de carbon, se micșorează odată cu creșterea temperaturii..
O placă de oțel are dimensiuni de 3m x 5m. Dimineața și la umbră temperatura sa este de 14 ° C, dar la prânz Soarele îl încălzește până la 52 ° C. Găsiți zona finală a plăcii.
Plecăm de la definiția coeficientului de expansiune a suprafeței:
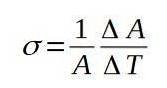
De aici rezolvăm variația zonei:
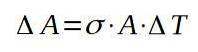
Apoi procedăm la înlocuirea valorilor respective pentru a găsi creșterea suprafeței prin creșterea temperaturii.
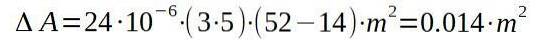
Adică, suprafața finală va fi de 15.014 metri pătrați.
Arătați că coeficientul de expansiune a suprafeței este aproximativ dublu față de coeficientul de expansiune liniară.
Să presupunem că pornim de la o placă dreptunghiulară cu dimensiunile lățime Lx și lungime Ly, atunci aria inițială a acesteia va fi A = Lx ∙ Ly
Atunci când placa suferă o creștere a temperaturii ΔT, atunci dimensiunile sale cresc, de asemenea, fiind noua lățime Lx 'și noua lungime Ly', astfel încât noua sa zonă va fi A '= Lx' ∙ Ly '
Variația suferită de zona plăcii datorită schimbării temperaturii va fi atunci
ΔA = Lx '∙ Ly' - Lx ∙ Ly
unde Lx '= Lx (1 + α ΔT) și Ly' = Ly (1 + α ΔT)
Adică, schimbarea zonei în funcție de coeficientul de expansiune liniară și schimbarea temperaturii vor fi:
ΔA = Lx (1 + α ΔT) ∙ Ly (1 + α ΔT) - Lx ∙ Ly
Acest lucru poate fi rescris ca:
ΔA = Lx ∙ Ly ∙ (1 + α ΔT) ² - Lx ∙ Ly
Dezvoltând pătratul și înmulțind avem următoarele:
ΔA = Lx ∙ Ly + 2α ΔT Lx ∙ Ly + (α ΔT) ² Lx ∙ Ly - Lx ∙ Ly
Deoarece α este de ordinul 10-6, atunci când este pătrat este de ordinul 10-12. Astfel, termenul pătratic din expresia de mai sus este neglijabil.
Apoi creșterea suprafeței poate fi aproximată prin:
ΔA ≈ 2α ΔT Lx ∙ Ly
Dar creșterea suprafeței în funcție de coeficientul de expansiune a suprafeței este:
ΔA = γ ΔT A
Din care derivă o expresie care leagă coeficientul de expansiune liniară cu coeficientul de expansiune al suprafeței.
γ ≈ 2 ∙ α
Nimeni nu a comentat acest articol încă.