
Simboluri și formule de diametru, cum se obține, circumferință
diametru Este linia dreaptă care trece prin centrul unei curbe plate închise sau o figură în două sau trei dimensiuni și care își unește și punctele opuse. De obicei, este o circumferință (o curbă plană), un cerc (o figură plană), o sferă sau un cilindru circular drept (obiecte tridimensionale).
Deși circumferința și cercul sunt de obicei luate ca sinonime, există o diferență între cei doi termeni. Circumferința este curba închisă care închide cercul, care îndeplinește condiția ca distanța dintre oricare dintre punctele sale și centru să fie aceeași. Această distanță nu este alta decât raza circumferinței. În schimb, cercul este o figură plană mărginită de circumferință.

În cazul circumferinței, cercului și sferei, diametrul este un segment drept care conține cel puțin trei puncte: centrul plus două puncte ale marginii circumferinței sau cercului, sau suprafața sferei.
Și în ceea ce privește cilindrul circular drept, diametrul se referă la secțiunea transversală, care împreună cu înălțimea, sunt cei doi parametri caracteristici ai săi.
Diametrul circumferinței și al cercului, simbolizat cu ø sau pur și simplu cu litera „D” sau „d”, este legat de perimetrul, conturul sau lungimea acestuia, care este notat cu litera L:
L = π.D = π. sau
Atâta timp cât există o circumferință, coeficientul dintre lungimea și diametrul său este numărul irațional π = 3,14159 ..., în acest fel:
π = L / D
Indice articol
- 1 Cum se obține diametrul?
- 1.1 Cifre cu lățime constantă
- 2 Diametrul unui cerc
- 2.1 - Exemplul 1
- 2.2 - Exemplul 2
- 3 Câte diametre are o circumferință?
- 4 Referințe
Cum se obține diametrul?
Când aveți desenul circumferinței sau al cercului sau direct obiectul circular, cum ar fi o monedă sau un inel, de exemplu, este foarte ușor să găsiți diametrul cu o riglă. Trebuie doar să vă asigurați că marginea riglei atinge două puncte de circumferință și centrul acesteia în același timp..
Un etrier, vernier sau etrier este foarte potrivit pentru măsurarea diametrelor externe și interne pe monede, cercuri, inele, piulițe, tuburi și multe altele..

Dacă în locul obiectului sau desenului său există date precum raza R, apoi înmulțind cu 2 avem diametrul. Și dacă se cunoaște lungimea sau perimetrul circumferinței, diametrul poate fi cunoscut și prin degajare:
D = 2.R
D = L / π
O altă modalitate de a găsi diametrul este cunoașterea ariei cercului, a suprafeței sferice, a secțiunii transversale a cilindrului, a zonei curbate a cilindrului sau a volumelor sferei sau cilindrului. Totul depinde de ce figură geometrică este. De exemplu, diametrul este implicat în următoarele zone și volume:
-Zona cercului: π. (D / 2)Două
-Suprafața sferică: 4π. (D / 2)Două
-Volumul sferei: (4/3) π. (D / 2)3
-Volumul cilindrului circular drept: π. (D / 2)Două.H (H este înălțimea cilindrului)
Cifre cu lățime constantă
Cercul este o figură plană cu lățime constantă, deoarece oriunde îl privești, lățimea este diametrul D. Cu toate acestea, există și alte figuri, probabil mai puțin cunoscute, a căror lățime este, de asemenea, constantă..
Să vedem mai întâi ce se înțelege prin lățimea unei figuri: este distanța dintre două linii paralele - linii de susținere -, care la rândul lor sunt perpendiculare pe direcția dată și care închid figura, după cum se arată în imaginea din stânga:
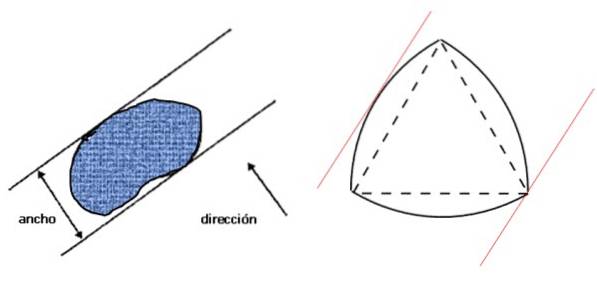
Lângă dreapta este triunghiul Reuleaux, care este o figură cu lățime constantă și care îndeplinește condiția specificată în figura din stânga. Dacă lățimea figurii este D, perimetrul său este dat de teorema lui Barbier:
L = π.D
Canalele din orașul San Francisco din California au forma unui triunghi Reuleaux, numit după inginerul german Franz Reuleaux (1829 - 1905). În acest fel, capacele nu pot cădea prin gaură și se folosește mai puțin material pentru realizarea lor, deoarece suprafața lor este mai mică decât cea a cercului:
A = (1- √3) .πDDouă = 0,705.DDouă
În timp ce pentru un cerc:
A = π. (D / 2)Două = (π / 4) DDouă= 0,785.DDouă
Dar acest triunghi nu este singura figură cu lățime constantă. Puteți construi așa-numitul Poligoane Reuleaux cu alți poligoane care au un număr impar de laturi.
Diametrul unei circumferințe

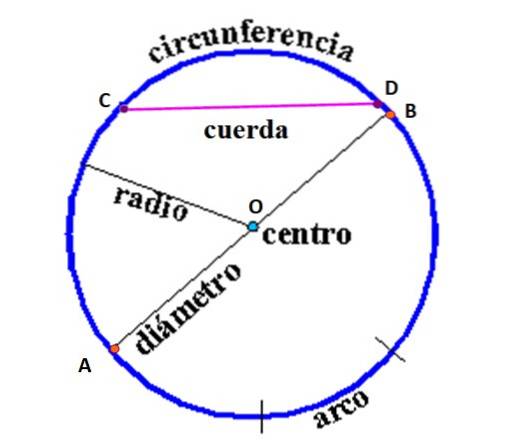
În figura următoare sunt elementele circumferinței, definite după cum urmează:
Şir: segment de linie care unește două puncte pe circumferință. În figură este acordul care unește punctele C și D, dar pot fi trasate infinite acorduri care unesc orice pereche de puncte de pe circumferință.
Diametru: este coarda care trece prin centru, unind două puncte ale circumferinței cu centrul O. Este cea mai lungă coardă a unei circumferințe, din acest motiv se numește „coardă majoră”.
Radio: segment de linie care unește centrul cu orice punct de pe circumferință. Valoarea sa, ca și diametrul, este constantă.
Circumferinţă: este mulțimea tuturor punctelor echidistante de la O.
Arc: definit ca un segment de circumferință delimitat de două raze (nu este desenat în figură).
- Exemplul 1
Dreptunghiul prezentat are o înălțime de 10 inci, care atunci când este rulat formează un cilindru circular drept al cărui diametru este de 5 inci. Răspunde la următoarele întrebări:
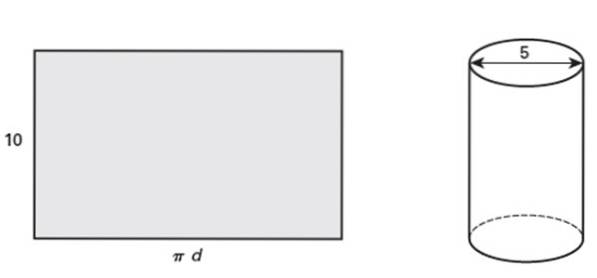
a) Care este conturul tubului?
b) Găsiți aria dreptunghiului
c) Calculați aria secțiunii transversale a cilindrului.
Solutie la
Conturul tubului este L = π.D = 5π in = 15.71 in.
Soluția b
Aria dreptunghiului este baza x inaltime, fiind baza L deja calculată și înălțimea este de 10 inci conform afirmației, prin urmare:
A = 15,71 în x 10 în = 157,1 înDouă.
Soluția c
În cele din urmă, aria solicitată este calculată astfel:
A = π. (D / 2)Două = (π / 4) DDouă = (π / 4) x (5 in.)Două= 19,63 in.Două.
- Exemplul 2
Calculați aria umbrită din Figura 5a. Pătratul are latura L.
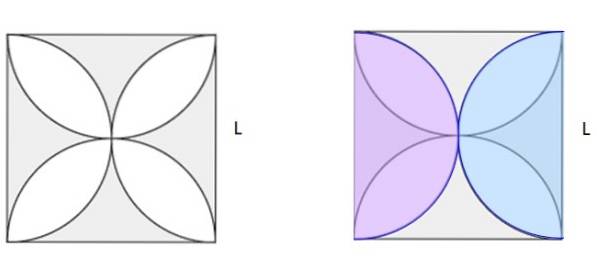
Soluţie
În figura 5b, două semicercuri de dimensiuni identice au fost desenate în roz și albastru, suprapuse pe figura originală. Între ele fac un cerc complet. Dacă găsiți aria pătratului și scădeți aria cercului, faceți zona umbrită din Figura 5b. Și uitându-ne atent, se dovedește că este jumătate din zona umbrită din 5a.
-Suprafața pătrată: LDouă
-Diametru semicerc: L
-Zona cercului: π. (L / 2)Două= (π / 4) LDouă
-Diferența de zone = jumătate din zona umbrită =
LDouă - (π / 4) LDouă = [(4 - π) / 4] LDouă= 0,2146 LDouă
-Suprafață umbrită = 2 x 0,2146 LDouă= 0,4292L2
Câte diametre are o circumferință?
Diametre infinite pot fi trasate pe o circumferință și oricare dintre ele măsoară la fel.
Referințe
- Antonio. Triunghiuri Reuleaux și alte curbe cu lățime constantă. Recuperat de pe: divulgators.com.
- Baldor, A. 2002. Geometrie și trigonometrie plană și spațială. Grupul Cultural Patria.
- Jiménez, R. Matematica II. Geometrie și trigonometrie. Al 2-lea. Ediție. Pearson.
- Wikipedia. Triunghiul Reuleaux. Recuperat de pe: es.wikipedia.org.
- Wolfram MathWorld. Diametru. Recuperat de pe: mathworld.wolfram.com.
Nimeni nu a comentat acest articol încă.