
Distribuții de probabilități discrete Caracteristici, exerciții
distribuții de probabilitate discrete sunt o funcție care atribuie fiecărui element al lui X (S) = x1, x2, ..., xi, ..., unde X este o variabilă aleatorie discretă dată și S este spațiul său de eșantionare, probabilitatea ca respectivul eveniment să apară. Această funcție f a lui X (S) definită ca f (xi) = P (X = xi) este uneori numită funcția de probabilitate a masei.
Această masă de probabilități este în general reprezentată sub formă de tabel. Deoarece X este o variabilă discretă aleatorie, X (S) are un număr finit de evenimente sau infinit numărabil. Printre cele mai comune distribuții de probabilitate discrete avem distribuția uniformă, distribuția binomială și distribuția Poisson.
Indice articol
- 1 Caracteristici
- 2 tipuri
- 2.1 Distribuția uniformă pe n puncte
- 2.2 Distribuția binomială
- 2.3 Distribuția Poisson
- 2.4 Distribuția hipergeometrică
- 3 exerciții rezolvate
- 3.1 Primul exercițiu
- 3.2 Al doilea exercițiu
- 3.3 Al treilea exercițiu
- 3.4 Al treilea exercițiu
- 4 Referințe
Caracteristici
Funcția de distribuție a probabilității trebuie să îndeplinească următoarele condiții:
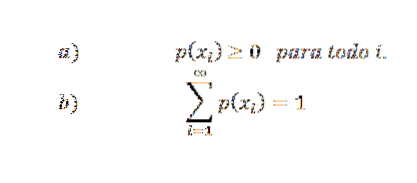
Mai mult, dacă X ia doar un număr finit de valori (de exemplu x1, x2,…, xn), atunci p (xi) = 0 dacă i> ny, prin urmare, seria infinită a condiției b devine o serie finită.
Această funcție îndeplinește, de asemenea, următoarele proprietăți:
Fie B un eveniment asociat cu variabila aleatoare X. Aceasta înseamnă că B este conținut în X (S). Mai exact, să presupunem că B = xi1, xi2, .... Prin urmare:
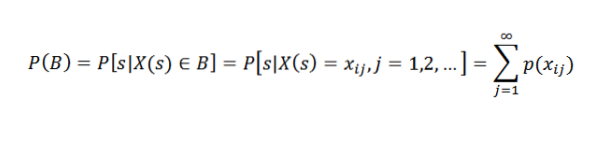
Cu alte cuvinte: probabilitatea unui eveniment B este egală cu suma probabilităților rezultatelor individuale asociate cu B.
Din aceasta putem concluziona că dacă a < b, los sucesos (X ≤ a) y (a < X ≤ b) son mutuamente excluyentes y, además, su unión es el suceso (X ≤ b), por lo que tenemos:
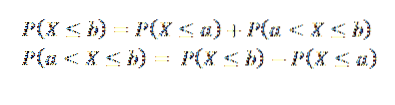
Tipuri
Distribuție uniformă pe n puncte
Se spune că o variabilă aleatorie X urmează o distribuție caracterizată prin aceea că este uniformă în n puncte dacă fiecărei valori i se atribuie aceeași probabilitate. Funcția sa de masă de probabilitate este:
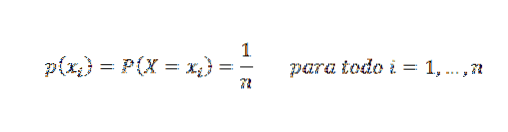
Să presupunem că avem un experiment care are două rezultate posibile, poate fi aruncarea unei monede ale cărei rezultate posibile sunt capete sau cozi sau alegerea unui număr întreg al cărui rezultat poate fi un număr par sau unul impar; acest tip de experiment este cunoscut sub numele de teste Bernoulli.
În general, cele două rezultate posibile se numesc succes și eșec, unde p este probabilitatea de succes și 1-p este probabilitatea de eșec. Putem determina probabilitatea x succese în n teste Bernoulli care sunt independente una de alta cu următoarea distribuție.
Distribuție binomială
Este funcția care reprezintă probabilitatea de a obține x succese în n teste Bernoulli independente, a căror probabilitate de succes este p. Funcția sa de masă de probabilitate este:
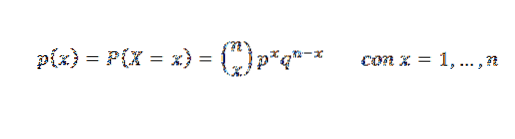
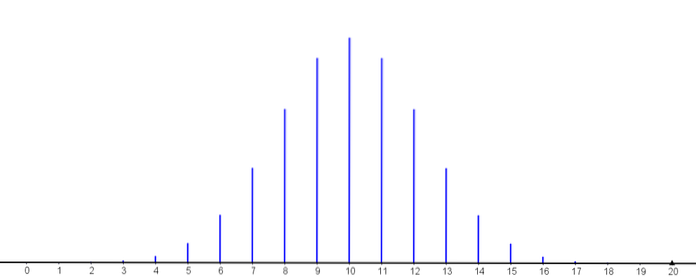
Următorul grafic reprezintă funcția de masă a probabilității pentru diferite valori ale parametrilor distribuției binomiale.
Următoarea distribuție își datorează numele matematicianului francez Simeon Poisson (1781-1840), care a obținut-o ca limită a distribuției binomiale.
Distribuția Poisson
Se spune că o variabilă aleatorie X are o distribuție Poisson a parametrului λ atunci când poate lua valorile întregi pozitive 0,1,2,3, ... cu următoarea probabilitate:
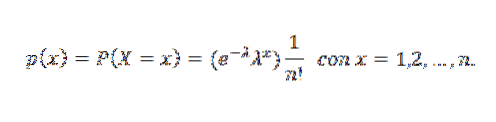
În această expresie, λ este numărul mediu corespunzător aparițiilor evenimentului pentru fiecare unitate de timp, și x este numărul de ori în care apare evenimentul.
Funcția sa de masă de probabilitate este:
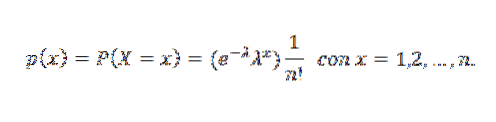
Apoi, un grafic care reprezintă funcția de masă a probabilității pentru diferite valori ale parametrilor distribuției Poisson.
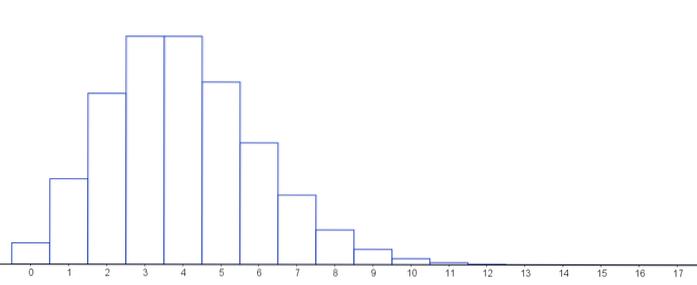
Rețineți că, atâta timp cât numărul de succese este scăzut și numărul de teste efectuate pe o distribuție binomială este mare, putem oricând să aproximăm aceste distribuții, deoarece distribuția Poisson este limita distribuției binomiale.
Principala diferență între aceste două distribuții este că, în timp ce binomul depinde de doi parametri - și anume, n și p-, Poisson depinde doar de λ, care este uneori numită intensitatea distribuției..
Până acum am vorbit doar despre distribuțiile de probabilitate pentru cazurile în care diferitele experimente sunt independente unele de altele; adică atunci când rezultatul unuia nu este afectat de vreun alt rezultat.
Când apare cazul experimentelor care nu sunt independente, distribuția hipergeometrică este foarte utilă.
Distribuția hipergeometrică
Fie N numărul total de obiecte ale unei mulțimi finite, dintre care putem identifica k într-un fel, formând astfel un subset K, al cărui complement este format din restul elementelor N-k.
Dacă alegem aleator n obiecte, variabila aleatoare X care reprezintă numărul de obiecte aparținând lui K în alegerea respectivă are o distribuție hipergeometrică a parametrilor N, n și k. Funcția sa de masă de probabilitate este:
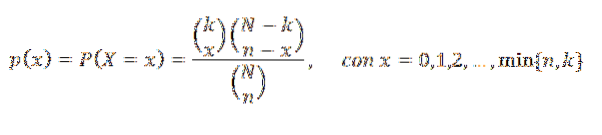
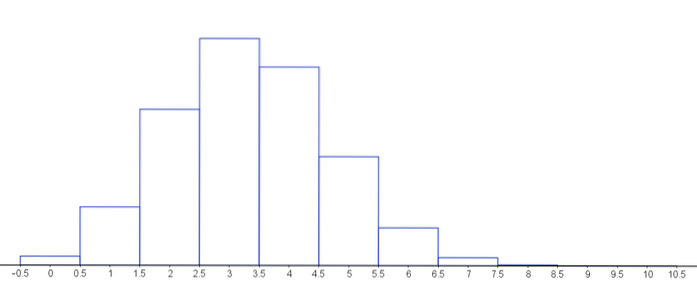
Următorul grafic reprezintă funcția de masă a probabilității pentru diferite valori ale parametrilor distribuției hipergeometrice.
Exerciții rezolvate
Primul exercițiu
Să presupunem că probabilitatea ca un tub radio (plasat într-un anumit tip de echipament) să funcționeze mai mult de 500 de ore este de 0,2. Dacă sunt testate 20 de tuburi, care este probabilitatea ca exact k dintre acestea să ruleze mai mult de 500 de ore, k = 0, 1,2, ..., 20?
Soluţie
Dacă X este numărul de tuburi care funcționează mai mult de 500 de ore, vom presupune că X are o distribuție binomială. Atunci
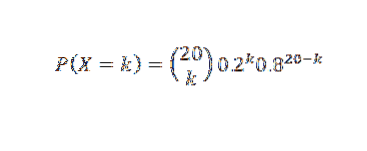
Așadar:

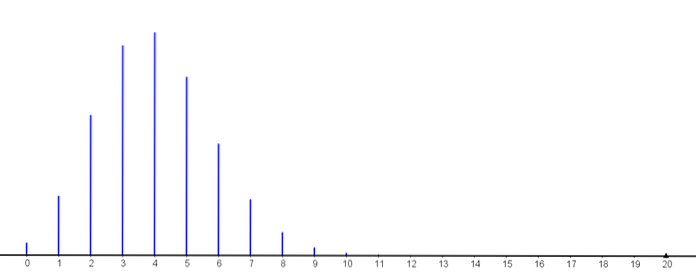
Pentru k≥11, probabilitățile sunt mai mici de 0,001
Astfel putem observa cum crește probabilitatea ca k dintre acestea să funcționeze mai mult de 500 de ore, până când atinge valoarea maximă (cu k = 4) și apoi începe să scadă..
Al doilea exercițiu
O monedă este aruncată de 6 ori. Când rezultatul este scump, vom spune că este un succes. Care este probabilitatea ca două capete să apară exact?
Soluţie
Pentru acest caz avem n = 6 și atât probabilitatea de succes, cât și eșecul sunt p = q = 1/2
Prin urmare, probabilitatea ca două capete să fie date (adică k = 2) este
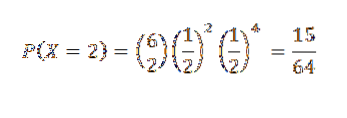
Al treilea exercițiu
Care este probabilitatea de a găsi cel puțin patru capete?
Soluţie
Pentru acest caz avem că k = 4, 5 sau 6
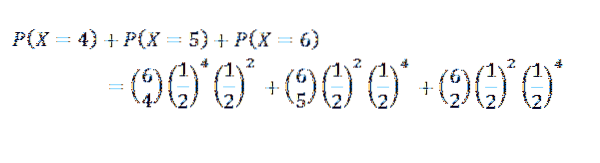
Al treilea exercițiu
Să presupunem că 2% din articolele produse într-o fabrică sunt defecte. Găsiți probabilitatea P că există trei articole defecte într-un eșantion de 100 de articole.
Soluţie
Pentru acest caz am putea aplica distribuția binomială pentru n = 100 și p = 0,02 obținând ca rezultat:
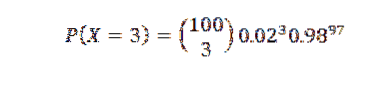
Cu toate acestea, deoarece p este mic, folosim aproximarea Poisson cu λ = np = 2. A) Da,
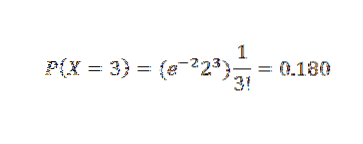
Referințe
- Kai Lai Chung. Teoria elementară a probabilității cu procese stochastice. Springer-Verlag New York Inc
- Kenneth.H. Rosen.Matematica discretă și aplicațiile sale. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Probabilități și aplicații statistice. S.A. ALHAMBRA MEXICANĂ.
- Dr. Seymour Lipschutz 2000 Rezolvarea problemelor de matematică discretă. McGRAW-HILL.
- Dr. Seymour Lipschutz Probleme de teorie și probabilitate. McGRAW-HILL.


Nimeni nu a comentat acest articol încă.