Ecuația generală a unei linii a cărei pantă este egală cu 2/3

Ecuația generală a unei linii L este următoarea: Ax + By + C = 0, unde A, B și C sunt constante, x este variabila independentă și și variabila dependentă.

Panta unei linii, în general notată cu litera m, care trece prin punctele P = (x1, y1) și Q = (x0, y0) este următorul coeficient m: = (y1-y0) / (x1 -x0 ).

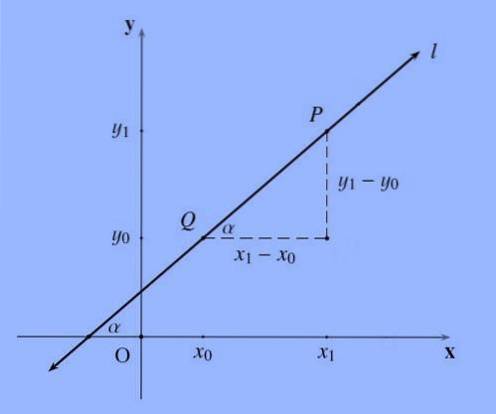
Panta unei linii, reprezintă într-un anumit mod înclinația; Mai formal, panta unei linii este tangenta unghiului pe care îl formează cu axa X..

Trebuie remarcat faptul că ordinea în care sunt denumite punctele este indiferentă, deoarece (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).

Panta unei linii

Dacă se cunosc două puncte prin care trece o dreaptă, este ușor să-i calculăm panta. Dar dacă aceste puncte nu sunt cunoscute?

Având în vedere ecuația generală a unei linii Ax + By + C = 0, panta acesteia este m = -A / B.

Care este ecuația generală a unei linii a cărei panta este 2/3?

Deoarece panta liniei este 2/3 atunci se stabilește egalitatea -A / B = 2/3, cu care putem vedea că A = -2 și B = 3. Deci ecuația generală a unei linii cu panta egală cu 2/3 este -2x + 3y + C = 0.

Ar trebui clarificat faptul că dacă se alege A = 2 și B = -3, se va obține aceeași ecuație. De fapt, 2x-3y + C = 0, care este egal cu precedentul înmulțit cu -1. Semnul lui C nu contează deoarece este o constantă generală.

O altă observație care se poate face este că pentru A = -4 și B = 6 se obține aceeași linie, în ciuda faptului că ecuația lor generală este diferită. În acest caz, ecuația generală este -4x + 6y + C = 0.

Există alte modalități de a găsi ecuația generală a liniei?

Raspunsul este da. Dacă panta unei linii este cunoscută, există două modalități, pe lângă cea anterioară, de a găsi ecuația generală.

Pentru aceasta, se utilizează ecuația punct-panta și ecuația panta-forfecare..

-Ecuația punct-panta: dacă m este panta unei drepte și P = (x0, y0) un punct prin care trece, atunci ecuația y-y0 = m (x-x0) se numește ecuația punct-panta.

-Ecuația Shear-Slope: dacă m este panta unei linii și (0, b) este tăierea liniei cu axa Y, atunci ecuația y = mx + b se numește ecuația Shear-Slope.

Folosind primul caz, se obține că ecuația punct-panta a unei linii a cărei panta este 2/3 este dată de expresia y-y0 = (2/3) (x-x0).

Pentru a ajunge la ecuația generală, înmulțiți cu 3 pe ambele părți și toți termenii sunt grupați pe o parte a egalității, cu care se obține că -2x + 3y + (2 × 0-3y0) = 0 este ecuația generală a liniei, unde C = 2 × 0-3y0.

Dacă se folosește al doilea caz, se obține că ecuația Cut-Slope a unei linii a cărei panta este 2/3 este y = (2/3) x + b.

Din nou, înmulțind cu 3 pe ambele părți și grupând toate variabilele, obținem -2x + 3y-3b = 0. Aceasta din urmă este ecuația generală a liniei unde C = -3b.

De fapt, analizând atent ambele cazuri, se poate observa că al doilea caz este pur și simplu un caz particular al primului (când x0 = 0).

Referințe

1. Fleming, W. și Varberg, D. E. (1989). Precalcul Matematică. Prentice Hall PTR.
2. Fleming, W. și Varberg, D. E. (1989). Matematica Precalcul: o abordare de rezolvare a problemelor (2, Ed. Ilustrată). Michigan: Prentice Hall.
3. Kishan, H. (2005). Calcul integral. Editori și distribuitori din Atlantic.
4. Larson, R. (2010). Precalcul (8 ed.). Cengage Learning.
5. Leal, J. M. și Viloria, N. G. (2005). Geometrie analitică plană. Mérida - Venezuela: Editorial Venezolana C. A.
6. Pérez, C. D. (2006). Precalcul. Pearson Education.
7. Saenz, J. (2005). Calcul diferențial cu funcții transcendente timpurii pentru Știință și Inginerie (Ediția a II-a ed.). Ipotenuză.
8. Sullivan, M. (1997). Precalcul. Pearson Education.