
Caracteristici și exemple ale elipsoidelor
elipsoid este o suprafață din spațiu care aparține grupului de suprafețe cvadrice și a cărei ecuație generală este de forma:
ToporDouă + DeDouă + CzDouă + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0
Este echivalentul tridimensional al unei elipse, caracterizat prin faptul că are urme eliptice și circulare în unele cazuri speciale. Urmele sunt curbele obținute prin intersecția elipsoidului cu un plan.

În plus față de elipsoid, mai există cinci cvadrici: hiperboloid cu o foaie și două coli, două tipuri de paraboloid (hiperbolic și eliptic) și conul eliptic. Urmele sale sunt, de asemenea, conice.
Elipsoidul poate fi exprimat și prin ecuația standard în coordonate carteziene. Un elipsoid centrat la origine (0,0,0) și exprimat în acest fel, seamănă cu elipsa, dar cu un termen suplimentar:

Valorile la, b Da c sunt numere reale mai mari decât 0 și reprezintă cele trei semi-axe ale elipsoidului.
Indice articol
- 1 Caracteristicile elipsoidului
- 1.1 - Ecuația standard
- 1.2 - Ecuații parametrice ale elipsoidului
- 1.3 - Urme ale elipsoidului
- 1.4 - Volum
- 2 Cazuri speciale ale elipsoidului
- 2.1 Elipsoidul de referință
- 2.2 Exemplu numeric
- 3 Referințe
Caracteristicile elipsoidelor
- Ecuația standard
Ecuația standard în coordonate carteziene pentru elipsa centrată în punct (h, k, m) este:

- Ecuații parametrice ale elipsoidului
În coordonate sferice, elipsoidul poate fi descris după cum urmează:
x = a sin sin. cos φ
y = b sin θ. sen φ
z = c cos θ
Semiaxele elipsoidului rămân a, b și c, în timp ce parametrii sunt unghiurile θ și φ din următoarea figură:

- Urme ale elipsoidului
Ecuația generală a unei suprafețe în spațiu este F (x, y, z) = 0, iar urmele suprafeței sunt curbele:
- x = c; F (c, y, z) = 0
- y = c; F (x, c, z) = 0
- z = c; F (x, y, c) = 0
În cazul unui elipsoid, astfel de curbe sunt elipse și uneori cercuri.
- Volum
Volumul V al elipsoidului este dat de (4/3) π ori produsul celor trei semiaxe ale sale:
V = (4/3) π. abc
Cazuri speciale ale elipsoidului
-Un elipsoid devine o sferă atunci când toate semi-axele au aceeași dimensiune: a = b = c ≠ 0. Acest lucru are sens, deoarece elipsoidul este ca o sferă care a fost întinsă diferit de-a lungul fiecărei axe..
-Sferoidul este un elipsoid în care două dintre semi-axe sunt identice și a treia este diferită, de exemplu ar putea fi a = b ≠ c.
Sferoidul mai este numit și elipsoid de revoluție, deoarece poate fi generat prin rotirea elipselor în jurul unei axe.
Dacă axa de rotație coincide cu axa majoră, sferoidul este prolata, dar dacă coincide cu axa minoră, este oblat:

Măsura aplatizării sferoidului (elipticitate) este dată de diferența de lungime dintre cele două semi-axe, exprimată sub formă fracționată, adică este unitatea de aplatizare, dată de:
f = (a - b) / a
În această ecuație, a reprezintă axa semi-majoră și b axa semi-minoră, amintiți-vă că a treia axă este egală cu una dintre acestea pentru un sferoid. Valoarea lui f este cuprinsă între 0 și 1 și pentru un sferoid trebuie să fie mai mare de 0 (dacă ar fi egal cu 0 am avea pur și simplu o sferă).
Elipsoidul de referință
Planetele și stelele, în general, nu sunt de obicei sfere perfecte, deoarece mișcarea de rotație din jurul axelor lor aplatizează corpul la poli și îl bombează la ecuator..
De aceea Pământul se dovedește a fi ca un sferoid oblat, deși nu la fel de exagerat ca cel din figura anterioară, iar la rândul său, gigantul gazos Saturn este cea mai plată dintre planetele din sistemul solar.
Deci, un mod mai realist de a reprezenta planetele este să presupunem că acestea sunt ca un sferoid sau elipsoid de revoluție, a cărui axă semi-majoră este raza ecuatorială și axa semi-minoră raza polară..
Măsurătorile atent făcute pe glob au făcut posibilă construirea elipsoid de referință a Pământului ca cel mai precis mod de a-l lucra matematic.
Stelele au și mișcări de rotație care le conferă forme mai mult sau mai puțin aplatizate. Steaua rapidă Achernar, cea de-a opta cea mai strălucitoare stea din cerul nopții, din constelația sudică Eridanus este remarcabil de eliptică în comparație cu majoritatea. Suntem la 144 de ani lumină de noi.
La cealaltă extremă, în urmă cu câțiva ani, oamenii de știință au găsit cel mai sferic obiect găsit vreodată: steaua Kepler 11145123, la 5000 de ani lumină distanță, de două ori mai mare decât Soarele nostru și o diferență între semi-axe de doar 3 km. Așa cum era de așteptat, se rotește și mai lent.
În ceea ce privește Pământul, acesta nu este nici un sferoid perfect datorită suprafeței sale accidentate și a variațiilor locale ale gravitației. Acesta este motivul pentru care există mai multe sferoide de referință disponibile și la fiecare sit este ales cel mai potrivit geografiei locale..
Ajutorul sateliților este de neprețuit în crearea unor modele din ce în ce mai exacte ale formei Pământului, datorită lor se știe, de exemplu, că polul sud este mai aproape de ecuator decât polul nord..
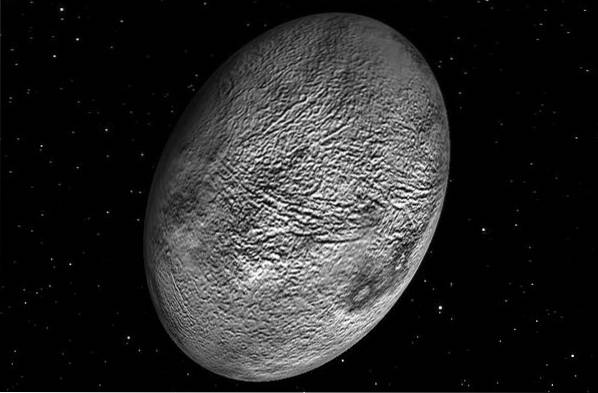
Exemplu numeric
Datorită rotației Pământului se generează o forță centrifugă care îi conferă forma unui elipsoid alungit, în locul unei sfere. Se știe că raza ecuatorială a Pământului este de 3963 mile, iar raza polară este de 3942 mile..
Găsiți ecuația urmei ecuatoriale, cea a acestui elipsoid și măsura aplatizării sale. De asemenea, comparați cu elipticitatea lui Saturn, cu datele furnizate mai jos:
-Raza ecuatorială a lui Saturn: 60268 km
-Raza polară Saturn: 54.364 km
Soluţie
Este necesar un sistem de coordonate, pe care îl vom presupune centrat pe origine (centrul Pământului). Vom presupune axa verticală z și urmele care corespund ecuatorului se află pe planul xy, echivalent cu planul z = 0.
În planul ecuatorial semi-axele a și b sunt egale, deci a = b = 3963 mile, în timp ce c = 3942 mile. Acesta este un caz special: un sferoid centrat în punctul (0,0,0) așa cum sa menționat mai sus.
Urma ecuatorială este un cerc de rază R = 3963 mile, centrat la origine. Se calculează făcând z = 0 în ecuația standard:

Și ecuația standard a elipsoidului terestru este:

F Teren = (a - b) / a = (3963-3942) mile / 3963 mile = 0,0053
F Saturn = (60268-54363) km / 60268 km = 0,0980
Rețineți că elipticitatea f este o cantitate adimensională.
Referințe
- ArcGIS pentru desktop. Sferoide și sfere. Recuperat de pe: desktop.arcgis.com.
- BBC World. Misterul celui mai sferic obiect descoperit vreodată în Univers. Recuperat de pe: bbc.com.
- Larson, R. Calcul și geometrie analitică. Ediția a șasea. Volumul 2. McGraw Hill.
- Wikipedia. Elipsoid. Recuperat de pe: en.wikipedia.org.
- Wikipedia. Sferoid. Recuperat de pe: en.wikipedia.org.

Nimeni nu a comentat acest articol încă.