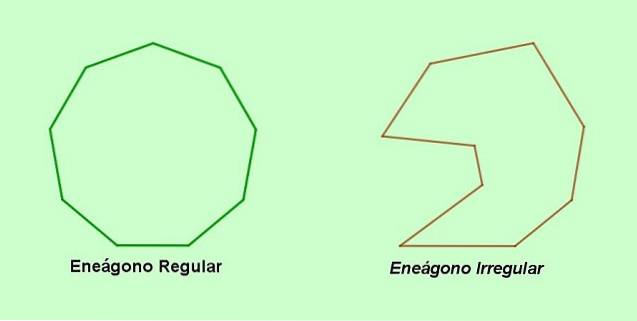
A eneagon este un poligon cu nouă laturi și nouă vârfuri, care poate fi sau nu regulat. Numele eneágono provine din greacă și este alcătuit din cuvintele grecești ennea (nouă și gonon (unghi).
Un nume alternativ pentru poligonul cu nouă fețe este nonagon, un cuvânt care provine din latină nonus (nouă și gonon (vârf). Pe de altă parte, dacă laturile sau unghiurile enegonului sunt inegale între ele, atunci avem un enegon neregulat. Dacă, pe de altă parte, cele nouă laturi și cele nouă unghiuri ale enegonului sunt egale, atunci este a enegon regulat.
Indice articol
Pentru un poligon cu n laturi, suma unghiurilor sale interioare este:
(n - 2) * 180º
În enegon ar fi n = 9, deci suma unghiurilor sale interne este:
Sa = (9 - 2) * 180º = 7 * 180º = 1260º
În orice poligon, numărul diagonalelor este:
D = n (n - 3) / 2 și în cazul enegonului, deoarece n = 9, atunci avem acel D = 27.
În eneagonul regulat sau nonagon există nouă (9) unghiuri interne de măsură egală, prin urmare fiecare unghi măsoară o nouăime din suma totală a unghiurilor interne.
Măsura unghiurilor interne ale unui enegon este apoi 1260º / 9 = 140º.
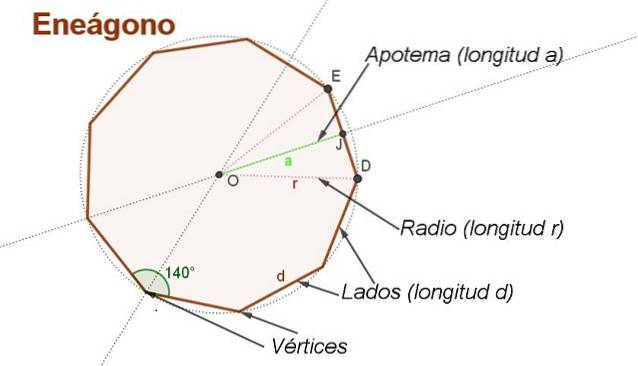
Pentru a obține formula pentru zona unui enegon obișnuit cu lateral d este convenabil să realizați câteva construcții auxiliare, precum cele prezentate în figura 2.
Centrul este situat SAU trasând bisectoarele a două laturi adiacente. Centrul SAU echidistant de vârfuri.
O rază de lungime r este segmentul care merge de la centru SAU la un vârf al enegonului. Razele sunt prezentate în figura 2. OD Da OE de lungime r.
Apotema este segmentul care merge de la centru la punctul mediu al unei părți a enegonului. De exemplu JO este o apotemă a cărei lungime este la.
Considerăm triunghiul ODĂ din figura 2. Aria acestui triunghi este produsul bazei sale DIN pentru înălțime JO împărțit la 2:
Zonă ODĂ = (DE * JO) / 2 = (d * a) / 2
Deoarece există 9 triunghiuri de suprafață egală în enegon, se concluzionează că aria aceleiași este:
Zona Eneagon = (9/2) (d * a)
Dacă se cunoaște doar lungimea d a laturilor enegonului, atunci este necesar să se găsească lungimea apotemului pentru a putea aplica formula din secțiunea anterioară.
Considerăm triunghiul OCHI dreptunghi în J (vezi figura 2). Dacă se aplică raportul trigonometric tangent, obținem:
asa de(∡OEJ) = JO / Ex.
Unghiul ∡OEJ = 140º / 2 = 70º, să fie EO bisectoare a unghiului intern al enegonului.
Pe de altă parte, JO este apotema lungimii la.
Apoi ca. J este punctul de mijloc al ED rezultă că EJ = d / 2.
Înlocuind valorile anterioare în relația tangentă avem:
bronz (70º) = a / (d / 2).
Acum ștergem lungimea apotemului:
a = (d / 2) bronz (70º).
Rezultatul anterior este înlocuit în formula zonei pentru a obține:
Zona Eneagon = (9/2) (d * a) = (9/2)( d * (d / 2) bronz (70º))
În cele din urmă, găsim formula care permite obținerea ariei enegonului regulat dacă se cunoaște doar lungimea d din laturile sale:
Zona Eneagon = (9/4) dDouă bronz (70º) = 6,1818 dDouă
Perimetrul unui poligon este suma laturilor sale. În cazul enegonului, fiecare dintre părți măsoară o lungime d, perimetrul său va fi suma de nouă ori d, și anume:
Perimetru = 9 d
Având în vedere triunghiul OCHI dreptunghi în J (vezi figura 2), se aplică raportul trigonometric al cosinusului:
cos (∡OEJ) = Ex / OE = (d / 2) / r
De unde se obține:
d = 2r cos (70º)
Înlocuind acest rezultat, obținem formula perimetrului în funcție de raza enegonului:
Perimetru = 9 d = 18 r cos (70º) = 6.1564 r
1- Pentru a construi un eneagon regulat, cu o riglă și o busolă, începeți de la circumferință c care circumscrie enegonul. (vezi figura 3)
2- Două linii perpendiculare sunt trasate prin centrul O al circumferinței. Apoi, intersecțiile A și B ale uneia dintre linii sunt marcate cu circumferința.
3- Cu busola, centrată pe interceptarea B și deschidere egală cu raza BO, se trasează un arc care interceptează circumferința inițială într-un punct C.
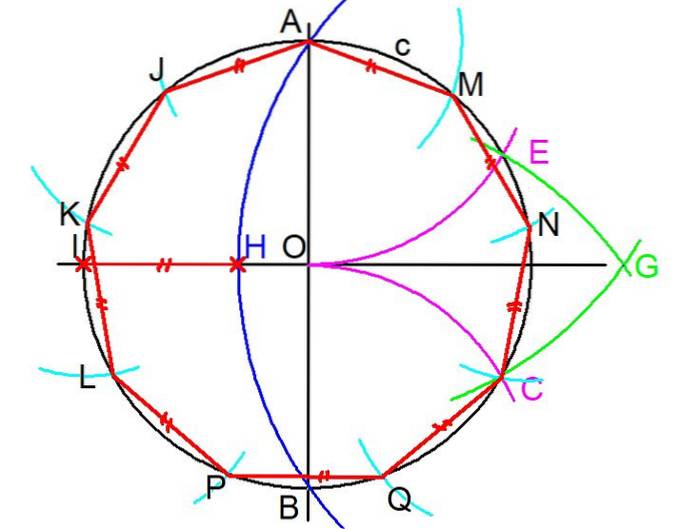
4- Pasul anterior se repetă, dar făcând un centru la A și raza AO, se trasează un arc care interceptează circumferința c în punctul E.
5- Cu deschiderea AC și centrul în A se trasează un arc de circumferință. În mod similar cu deschiderea BE și centrul B este trasat un alt arc. Intersecția acestor două arce este marcată ca punctul G.
6- Centrarea la G și deschiderea GA, se trasează un arc care interceptează axa secundară (orizontală în acest caz) în punctul H. Intersecția axei secundare cu circumferința originală c este marcată ca I.
7- Lungimea segmentului IH este egală cu lungimea d a laturii enegonului.
8- Cu deschiderea busolei IH = d, se desenează succesiv arcurile de centru A rază AJ, centru J rază AK, centru K rază KL și centru L rază LP.
9- În mod similar, începând de la A și din partea dreaptă, sunt trasate arcuri de rază IH = d care marchează punctele M, N, C și Q pe circumferința originală c.
10- În cele din urmă sunt trasate segmentele AJ, JK, KL, LP, AM, MN, NC, CQ și în cele din urmă PB.
Trebuie remarcat faptul că metoda de construcție nu este în totalitate exactă, deoarece se poate verifica că ultima latură PB este cu 0,7% mai lungă decât celelalte laturi. Până în prezent, nu există nicio metodă de construcție cunoscută cu o riglă și busolă care este 100% precisă..
Iată câteva exemple lucrate.
Vrei să construiești un enegon obișnuit ale cărui laturi măsoară 2 cm. Ce rază trebuie să aibă circumferința care o circumscrie, astfel încât atunci când se aplică construcția descrisă anterior, se obține rezultatul dorit?
Soluţie:
Într-o secțiune anterioară, s-a dedus formula care raportează raza r a cercului circumscris cu latura d a unui enegon regulat:
d = 2r cos (70º)
Rezolvând pentru r din expresia anterioară avem:
r = d / (2 cos (70º)) = 1,4619 * d
Înlocuind valoarea d = 2 cm în formula anterioară, se obține o rază r de 2,92 cm.
Care este aria unui enegon obișnuit cu o latură de 2 cm?
Soluţie:
Pentru a răspunde la această întrebare, trebuie să ne referim la formula, prezentată anterior, care ne permite să găsim aria unui enegon cunoscut după lungimea d a laturii sale:
Zona Eneagon = (9/4) dDouă bronz (70º) = 6,1818 dDouă
Înlocuind d cu valoarea sa de 2 cm în formula anterioară, obținem:
Zona Eneagon = 24,72 cm
Nimeni nu a comentat acest articol încă.