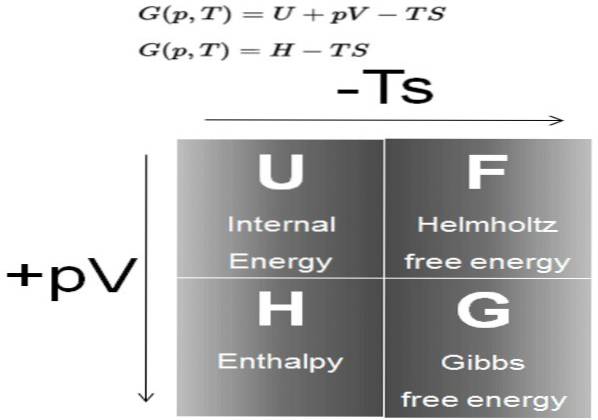
Energie liberă Gibbs (denumit în mod obișnuit G) este un potențial termodinamic definit ca diferența de entalpie H, minus produsul temperaturii T, de entropia S a sistemului:
G = H - T S
Energia liberă Gibbs este măsurată în Jouli (conform sistemului internațional), în erg-uri (pentru sistemul cegezimal de unități), în calorii sau în volți de electroni (pentru electro Volți).
În procesele care apar la presiune și temperatură constante, variația energiei libere Gibbs este ΔG = ΔH - T ΔS. În astfel de procese, (G) reprezintă energia disponibilă în sistem care poate fi convertită în muncă.
De exemplu, în reacțiile chimice exoterme, entalpia scade în timp ce entropia crește. În funcția Gibbs acești doi factori sunt contracarați, dar numai atunci când energia Gibbs scade reacția apare spontan..
Deci, dacă variația lui G este negativă, procesul este spontan. Când funcția Gibbs atinge nivelul minim, sistemul atinge o stare stabilă de echilibru. Pe scurt, într-un proces pentru care presiunea și temperatura rămân constante, putem afirma:
- Dacă procesul este spontan, atunci ΔG < 0
- Când sistemul este în echilibru: ΔG = 0
- Într-un proces non-spontan G crește: ΔG> 0.
Indice articol
Energia liberă Gibbs (G) este calculată utilizând definiția dată la început:
G = H - T⋅S
La rândul său, entalpia H este un potențial termodinamic definit ca:
H = U + P V
Apoi, se va face o analiză pas cu pas, pentru a cunoaște variabilele independente ale cărora energia Gibbs este o funcție:
1- Din prima lege a termodinamicii avem că energia internă U este legată de entropia S a sistemului și de volumul său V pentru procese reversibile prin relația diferențială:
dU = dQ - dW = TdS - PdV
Din această ecuație rezultă că energia internă U este o funcție a variabilelor S și V:
U = U (S, V)
2- Pornind de la definiția lui H și luând diferențialul, obținem:
dH = dU + d (P V) = dU + VdP + PdV
3- Înlocuind expresia pentru dU obținută în (1) avem:
dH = TdS - PdV + VdP + PdV = TdS + VdP
Din aceasta se concluzionează că entalpia H depinde de entropia S și de presiunea P, adică:
H = H (S, P)
4- Acum diferențialul total al energiei libere Gibbs se calculează obținând:
dG = dH -TdS -SdT = TdS + VdP -TdS -SdT
În cazul în care dH a fost înlocuit cu expresia găsită în (3).
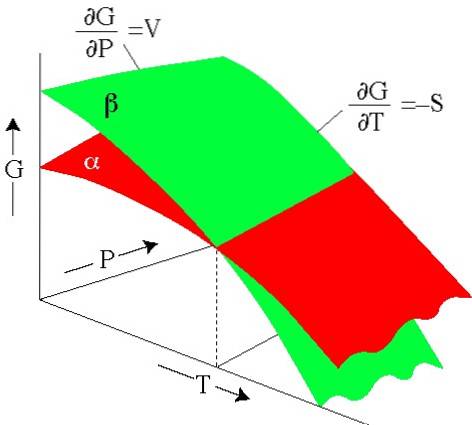
5- În cele din urmă, atunci când simplificăm, obținem: dG = VdP - SdT, fiind clar că energia liberă G depinde de presiune și de temperatura T ca:
G = G (P, T)
Din analiza din secțiunea anterioară, rezultă că energia internă a unui sistem este o funcție de entropie și volum:
U = U (S, V)
Apoi diferențialul de SAU va fi:
dU = ∂SU |V dS + ∂VU |S dV = TdS - PdV
Din această expresie derivată parțială, pot fi derivate așa-numitele relații termodinamice Maxwell. Derivatele parțiale se aplică atunci când o funcție depinde de mai multe variabile și se calculează cu ușurință prin aplicarea teoremei din secțiunea următoare.
∂VT |S = -∂SP |V
Pentru a ajunge la această relație, Teorema Clairaut-Schwarz privind derivatele parțiale, care prevede următoarele:
"Derivatele mixte de ordinul doi cu variabilele interschimbate sunt egale, atâta timp cât funcțiile care urmează să fie derivate sunt continue și diferențiate".
Pe baza a ceea ce este prezentat la punctul 3 din secțiunea anterioară:
H = H (S, P) și dH = TdS + VdP
Se poate obține:
∂PT |S = ∂SV |P
Procedăm în mod similar cu energia liberă Gibbs G = G (P, T) și cu energie gratuită Helmholtz F = F (T, V) pentru a obține celelalte două relații termodinamice Maxwell.
1- Asociat cu energia internă U: ∂VT |S = -∂SP |V
2- Cel obținut din entalpia H: ∂PT |S = ∂SV |P
3- Legat de energia Helmholtz F: ∂TP |V = ∂VS |T
4- Legat de energia liberă Gibbs G: ∂TV |P = -∂PS |T
Calculați variația energiei libere Gibbs pentru 2 moli de gaz ideal la o temperatură de 300K în timpul unei expansiuni izoterme care duce sistemul de la un volum inițial de 20 litri la un volum final de 40 litri.
Amintind definiția energiei libere Gibbs avem:
G = H - T S
Atunci o variație finită a lui F va fi:
ΔG = ΔH - T ΔS, deoarece ΔT = 0
În gazele ideale, entalpia depinde doar de temperatura sa absolută, dar din moment ce este un proces izoterm, atunci ΔH = 0 și ΔG = - T ΔS.
Pentru gazele ideale, schimbarea entropiei unui proces izoterm este:
ΔS = nR ln (VDouă/ V1)
Cea aplicată în cazul acestui exercițiu rămâne:
ΔS = 2 moli x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Atunci putem obține schimbarea energiei Helmholtz:
ΔG = - 300K x 11,53 J / K = -3457,70 J.
Luând în considerare faptul că energia liberă Gibbs este o funcție de temperatură și presiune G = G (T, P); determinați variația lui G în timpul unui proces în care temperatura nu se schimbă (izotermă) pentru n moli de gaz ideal monatomic.
După cum s-a demonstrat mai sus, schimbarea energiei Gibbs depinde doar de schimbarea temperaturii T și a volumului V, astfel încât o variație infinitesimală a acesteia este calculată în funcție de:
dG = -SdT + VdP
Dar dacă este un proces în care temperatura este constantă, atunci dF = + VdP, deci o variație finită a presiunii ΔP duce la o schimbare a energiei Gibbs dată de:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = + n R T ln (ΔP)
Folosind ecuația gazului ideal:
P V = n R T
În timpul unui proces izotermic se întâmplă că:
d (P V) = P dV + V dP = 0
Acesta este:
dP / P = - dV / V
Deci, rezultatul de mai sus poate fi scris în funcție de variația volumului ΔV:
ΔG = + ∫ VdP = + ∫ (n R T) dP / P = - ∫ (n R T) dV / V = -n R T ln (ΔV)
Având în vedere următoarea reacție chimică:
NDouă0 (g) + (3/2) ODouă (g) ↔️ 2NODouă (g) la temperatura T = 298 K.
Găsiți variația energiei libere Gibbs și, utilizând rezultatul obținut, indicați dacă este sau nu un proces spontan.
Iată pașii:
- Primul pas: entalpii de reacție
ΔHr = 2 * ΔH (NRDouă (g)) - ΔH (NDouă0 (g)) = 2 * 33,2-81,6 = -15,2kJ / mol
- Al doilea pas: variația entropiei reacției
ΔSr = 2 * S (NRDouă (g)) - S (NDouă0 (g)) - (3/2) S (ODouă (g)) = 2 * 240,1 - 220,1 - 1,5 * 205,2 = -47,7 J / (mol * K).
- Al treilea pas: variația funcției Gibbs
Această valoare va determina echilibrul dintre energia descrescătoare și entropia crescătoare pentru a ști dacă în cele din urmă reacția este spontană sau nu.
ΔGr = ΔHr - T ΔSr = -15,2 -298 * (- 47,7) = -985,4 J / mol
Deoarece este o variație negativă a energiei Gibbs, se poate concluziona că este o reacție spontană la temperatura de 298 K = 25 ºC.
Nimeni nu a comentat acest articol încă.