Unități de energie liberă Helmholtz, cum se calculează, exerciții rezolvate

Energie gratuită Helmholtz este un potențial termodinamic care măsoară munca utilă a unui sistem închis în condiții de temperatură și volum constante. Energia liberă Helmholtz este notată ca F y este definit ca diferența de energie internă SAU minus produsul temperaturii T prin entropie S:

F = U - T⋅S

Deoarece este energie, este măsurată în Jouli în Sistemul Internațional (SI), deși alte unități adecvate pot fi, de asemenea, erg-uri (CGS), calorii sau electron volți (eV).

Variația negativă a energiei Helmholtz în timpul unui proces este echivalată cu munca maximă pe care o poate face sistemul într-un proces izocoric, adică la volum constant. Când volumul nu este menținut constant, o parte din această lucrare poate fi realizată asupra mediului.

În acest caz, ne referim la lucrări în care volumul nu variază, cum ar fi lucrul electric: dW = Φdq, cu Φ ca potențial electric și q ca sarcină electrică.

Dacă și temperatura este constantă, energia Helmholtz este redusă la minimum atunci când se atinge echilibrul. Pentru toate acestea, energia Helmholtz este deosebit de utilă în procesele cu volum constant. În acest caz aveți:

- Pentru un proces spontan: ΔF < 0

- Când sistemul este în echilibru: ΔF = 0

- Într-un proces non-spontan: ΔF> 0.

Indice articol

• 1 Cum se calculează energia liberă Helmholtz??
  • 1.1 Procese spontane
• 2 exerciții rezolvate
  • 2.1 Exercițiul 1
  • 2.2 Exercițiul 2
• 3 Referințe

Cum se calculează energia liberă Helmholtz??

După cum sa menționat la început, energia Helmholtz este definită ca „energia internă U a sistemului, minus produsul temperaturii absolute T a sistemului, prin entropia S a sistemului”:

F = U - T⋅S

Este o funcție a temperaturii T și a volumului V. Pașii pentru a vizualiza acest lucru sunt după cum urmează:

- Plecând de la prima lege a termodinamicii, energia internă U este legată de entropia S a sistemului și de volumul său V pentru procese reversibile prin următoarea relație diferențială:

dU = dQ - dW = TdS - PdV

Din aceasta rezultă că energia internă U este o funcție a variabilelor S Da V, Prin urmare:

U = U (S, V)

- Acum luăm definiția lui F și este derivat:

dF = dU - d (TS) = dU - TdS - SdT

- Înlocuind acolo expresia diferențială obținută pentru dU în primul pas, rămâne:

dF = TdS - PoV - TdS - SdT = -SdT - PoV

- În cele din urmă, se concluzionează că F este o funcție a temperaturii T și a volumului V și poate fi exprimat ca:

F = F (T, V)

Procese spontane

Energia Helmholtz poate fi aplicată ca un criteriu general de spontaneitate în sisteme izolate, dar mai întâi este convenabil să specificați câteva concepte:

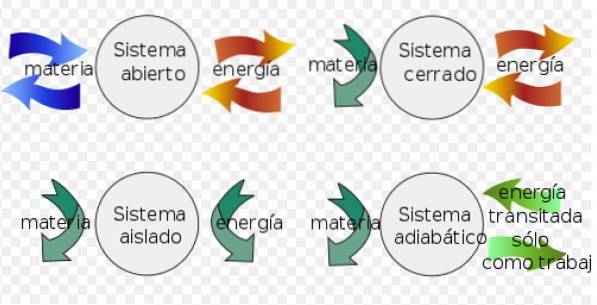
- A sistemul închis poate schimba energia cu mediul, dar nu poate schimba materia.

- În schimb a sistem izolat nu schimbă materia sau energia cu mediul.

- În cele din urmă a sistem deschis schimbați materia și energia cu mediul. 

În procesele reversibile, variația energiei interne se calculează după cum urmează:

dU = TdS - PoV

Să presupunem acum un proces la volum constant (izocoric), în care al doilea termen al expresiei anterioare are contribuție zero. De asemenea, trebuie amintit că, în conformitate cu Inegalitatea lui Clausius: 

dS ≥ dQ / T

O astfel de inegalitate se aplică unui sistem termodinamic izolat.

Deci, pentru un proces (reversibil sau nu) în care volumul rămâne constant, următoarele sunt adevărate:

T dS ≥ dU (la volum fix)

Ținând cont de faptul că:

dF = dU - T dS 

Vom avea faptul că într-un proces izocoric la temperatură constantă este satisfăcut că: dF ≤ 0, așa cum a fost indicat la început.

Deci, energia Helmholtz F este o cantitate descrescătoare într-un proces spontan, atâta timp cât este un sistem izolat. F atinge valoarea sa minimă și stabilă atunci când s-a atins echilibrul reversibil.

Exerciții rezolvate

Exercitiul 1

Calculați variația energiei libere Helmholtz F pentru 2 moli de gaz ideal la o temperatură de 300K în timpul unei expansiuni izoterme care duce sistemul de la un volum inițial de 20 litri la un volum final de 40 litri.

Soluţie

Pornind de la definiția lui F:

F = U - T S

Atunci o variație finită a lui F, numită ΔF, va fi:

ΔF = ΔU - T ΔS

Deoarece afirmația afirmă că temperatura este constantă: ΔT = 0. Acum, în gazele ideale, energia internă depinde doar de temperatura lor absolută, dar din moment ce este un proces izoterm, atunci ΔU = 0 Da ΔF = - T ΔS. Pentru gazele ideale, schimbarea entropiei unui proces izotermic este scrisă astfel: 

ΔS = n.R.ln (V_Două/ V₁)

Aplicând această expresie:

ΔS = 2 moli x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K

În cele din urmă, schimbarea energiei Helmholtz este:

ΔF = - T ΔS = - 300K x 11,53 J / K = -3457,70 J.

Exercițiul 2

În interiorul unui cilindru există un piston care îl împarte în două secțiuni și pe fiecare parte a pistonului există n aluniți ai unui gaz ideal monatomic, așa cum se arată în figura de mai jos.

Pereții cilindrilor sunt buni conductori de căldură (diatermici) și sunt în contact cu un rezervor de temperatură T_sau.

Volumul inițial al fiecărei secțiuni a cilindrilor este V_1i și V_2i, în timp ce volumele sale finale sunt V_1f și V_2f după deplasare cvasistatică. Pistonul este deplasat cu ajutorul unui piston care trece ermetic prin capacele celor două cilindri.

Se cere să găsiți:

a) Schimbarea energiei interne a gazului și munca depusă de sistem și

b) Variația energiei Helmholtz.

Solutie la

Deoarece pistonul se mișcă cvasi-static, forța externă aplicată asupra pistonului trebuie să echilibreze forța datorită diferenței de presiune din cele două secțiuni ale cilindrului..

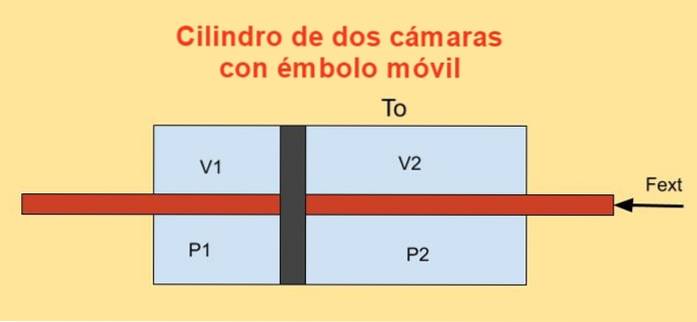
Treaba dW efectuată de forța externă F_ext în timpul unei schimbări infinitesimale dx este:

dW = - F_ext dx = (P₁ - P_Două) a dx = P₁ dV₁ + P_Două dV_Două

Unde a fost utilizată relația dV₁ = - dV_Două = a dx, fiind la zona pistonului. Pe de altă parte, variația energiei Helmholtz este: 

dF = -SdT - PdV

Deoarece temperatura nu se schimbă în timpul procesului, atunci dT = 0 Da dF = - PoV. Aplicând această expresie fiecărei secțiuni a cilindrului avem:

dW = P₁ dV₁ + P_Două dV_Două = - dF₁ - dF_Două

Fiind F₁  Da F_Două energiile Helmholtz din fiecare cameră.

Lucrarea finită W poate fi calculată din variația finită a energiei Helmholtz a fiecărei camere:

W = -ΔF₁ - ΔF_Două

Soluția b

Pentru a găsi schimbarea energiei Helmholtz, se folosește definiția: F = U - T S. Ca în fiecare cameră există un gaz ideal monatomic la temperatură constantă T_sau, energia internă nu se schimbă (ΔU = 0), astfel încât: ΔF = - T_sau ΔS. Ce este mai mult:

ΔS = nR ln (V_F/A văzut)

Asta când înlocuirea permite în cele din urmă munca efectuată să fie: 

W = -T_sau nR ln (V_1f / V_1i) -To nR ln (V_2f / V_2i) = -ΔF₁ -ΔF_Două

W = - To nR ln [(V_1f ⋅ V_1i) / (V_{2f .}V_2i)] = - ΔF_total

Fiind ΔF_total schimbarea totală a energiei Helmholtz.

Referințe

1. Castane E. Exerciții de energie gratuită. Recuperat de pe: lidiaconlaquimica.wordpress.com
2. Libretexturi. Energia Helmholtz. Recuperat de pe: chem.libretexts.org
3. Libretexturi. Ce sunt energiile gratuite. Recuperat de pe: chem.libretexts.org
4. Wikipedia. Energia Helmholtz. Recuperat de pe: es.wikipedia.com
5. Wikipedia. Energie gratuită Helmholtz. Recuperat de pe: en.wikipedia.com